Гипербола

ОПРЕДЕЛЕНИЕ
Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

ВЫВОД КАНОНИЧЕСКОГО УРАВНЕНИЯ ГИПЕРБОЛЫ (ПАСПОРТ)
Дано:
MF1 – MF2 = 2a, 2a < 2c
Составить:
Уравнение геометрического места точек.

РЕШЕНИЕ:
1) Выбор системы координат x0y

КАНОНИЧЕСКОЕ УРАВНЕНИЕ ГИПЕРБОЛЫ

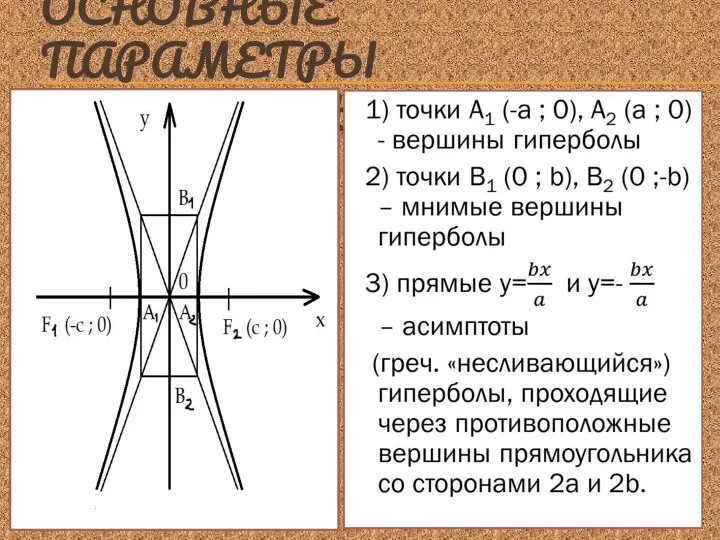
ОСНОВНЫЕ ПАРАМЕТРЫ ГИПЕРБОЛЫ

4) уравнение гиперболы содержит лишь чётные степени переменных x и y, значит, эта кривая обладает симметричностью относительно осей 0x и 0y, а значит, она обладает центральной симметрией относительно начала координат. Точка 0 – центр гиперболы.
5) отрезок A1A2 – действительная ось гиперболы; A1A2 = 2a
Доказательство:
MF1 – MF2 = 2a (свойство точек гиперболы)
A1F2 – A1F1 = 2a (свойство точек гиперболы)
A1F1 = A2F2 (из соображений симметрии)
A1F2 – A2F2 = 2a
A1A2 = 2a
6) можно доказать, что B1B2 = 2b, где B1B2 – мнимая ось гиперболы.

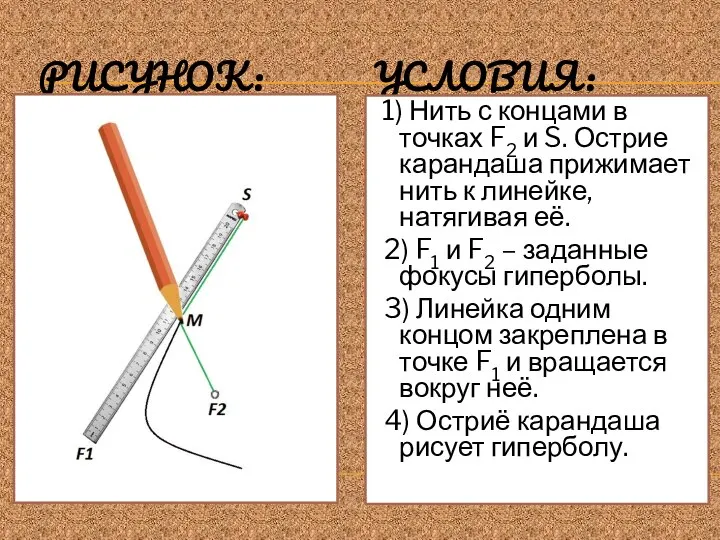
ПОСТРОЕНИЕ ГИПЕРБОЛЫ С ПОМОЩЬЮ НАТЯНУТОЙ НИТИ

РИСУНОК:
УСЛОВИЯ:
1) Нить с концами в точках F2 и S. Острие карандаша прижимает нить к линейке, натягивая её.
2) F1 и F2 – заданные фокусы гиперболы.
3) Линейка одним концом закреплена в точке F1 и вращается вокруг неё.
4) Остриё карандаша рисует гиперболу.

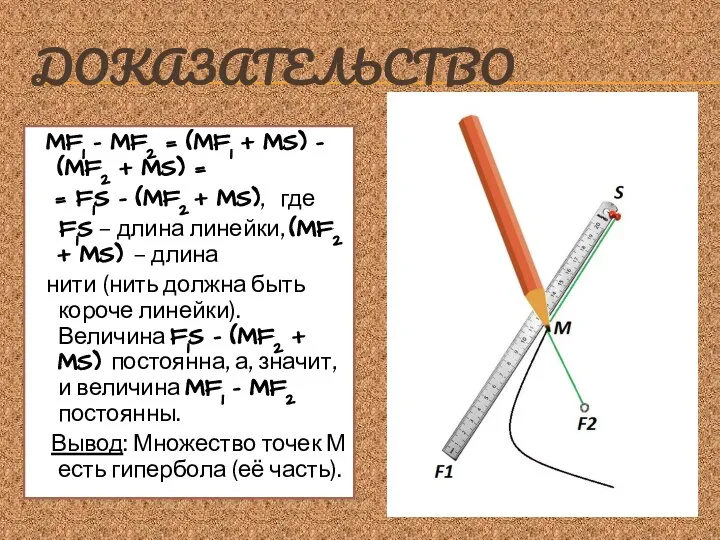
ДОКАЗАТЕЛЬСТВО
MF1 – MF2 = (MF1 + MS) – (MF2 + MS) =
= F1S – (MF2 + MS), где
F1S – длина линейки, (MF2 + MS) – длина
нити (нить должна быть короче линейки). Величина F1S – (MF2 + MS) постоянна, а, значит, и величина MF1 – MF2 постоянны.
Вывод: Множество точек М есть гипербола (её часть).

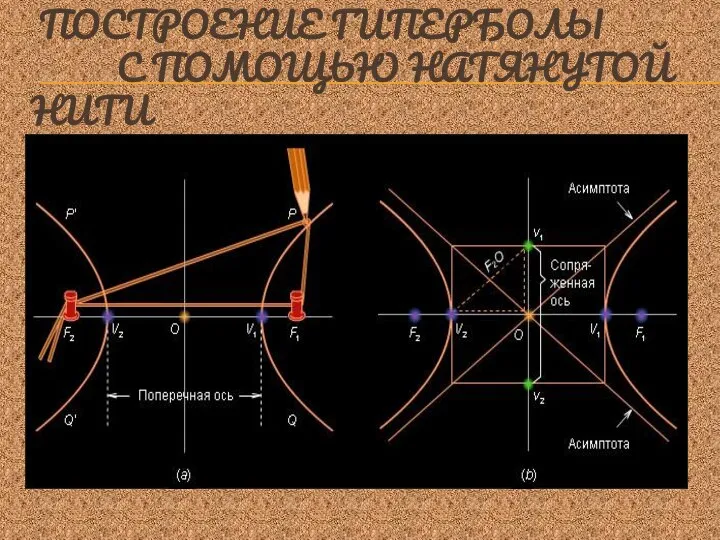
ПОСТРОЕНИЕ ГИПЕРБОЛЫ С ПОМОЩЬЮ НАТЯНУТОЙ НИТИ

ГИПЕРБОЛА КАК ОГИБАЮЩАЯ СЕМЕЙСТВА ПРЯМЫХ
Гиперболу, как и эллипс, можно построить с помощью метода сгибания листа бумаги, что указывает на взаимосвязь этих кривых.
На листе бумаги чертим окружность с центром в точке О и отмечаем точку А вне окружности.
Многократно сгибаем лист бумаги так, чтобы окружность проходила через точку А.
Гипербола – огибающая касательных (сгибов), а точки О и А – фокусы гиперболы.

ОПТИЧЕСКИЕ СВОЙСТВА ГИПЕРБОЛЫ
Оптическое свойство: Оптические лучи, исходящие из одного фокуса гиперболы, отразившись от нее кажутся исходящими из второго фокуса.
Фокальное свойство:
Отрезки, соединяющие точку гиперболы с её фокусами, составляют равные углы с касательной в точке X.
Дано:
Прямая l,
A не принадлежит l,
B не принадлежит l,
A и B – по разные стороны от прямой l.
Найти:
Точку X принадлежащую l, где (AX-BX) – наибольшая.

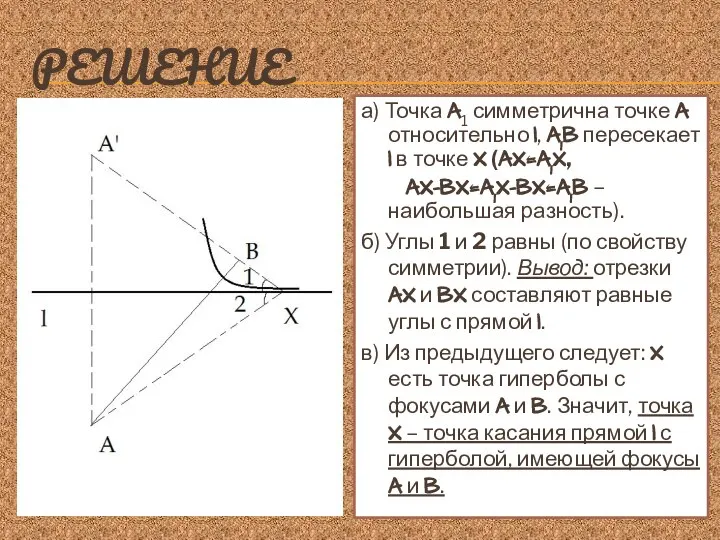
РЕШЕНИЕ
а) Точка A1 симметрична точке A относительно l, A1B пересекает l в точке X (AX=A1X,
AX-BX=A1X-BX=A1B – наибольшая разность).
б) Углы 1 и 2 равны (по свойству симметрии). Вывод: отрезки AX и BX составляют равные углы с прямой l.
в) Из предыдущего следует: X есть точка гиперболы с фокусами A и B. Значит, точка X – точка касания прямой l с гиперболой, имеющей фокусы A и B.

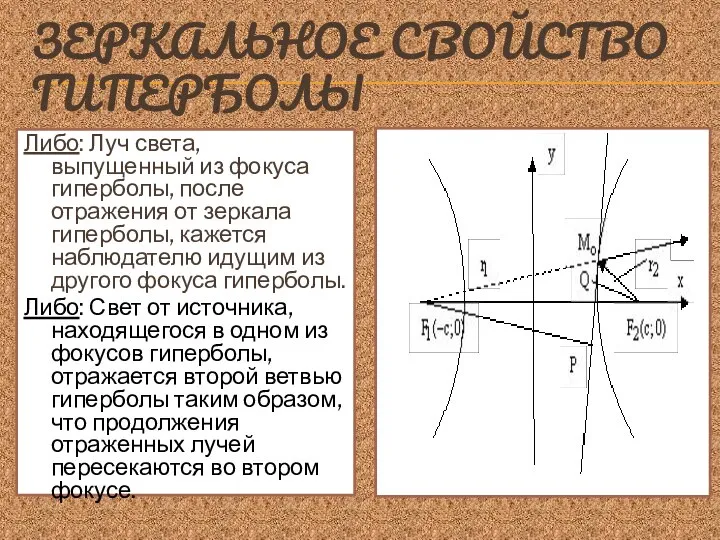
ЗЕРКАЛЬНОЕ СВОЙСТВО ГИПЕРБОЛЫ
Либо: Луч света, выпущенный из фокуса гиперболы, после отражения от зеркала гиперболы, кажется наблюдателю идущим из другого фокуса гиперболы.
Либо: Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.

ПРИМЕНЕНИЕ СВОЙСТВ ГИПЕРБОЛЫ
Зеркала, в сечении имеющие форму гипербол, используются в некоторых телескопах – рефлекторах, камерах специального назначения, а также в качестве отражателей карманных фонарей и прожекторов.
Свойство двуполостного гиперболоида вращения отражать лучи, направленные в один из фокусов, в другой фокус, используется в телескопах системы Кассегрена и в антеннах Кассегрена.

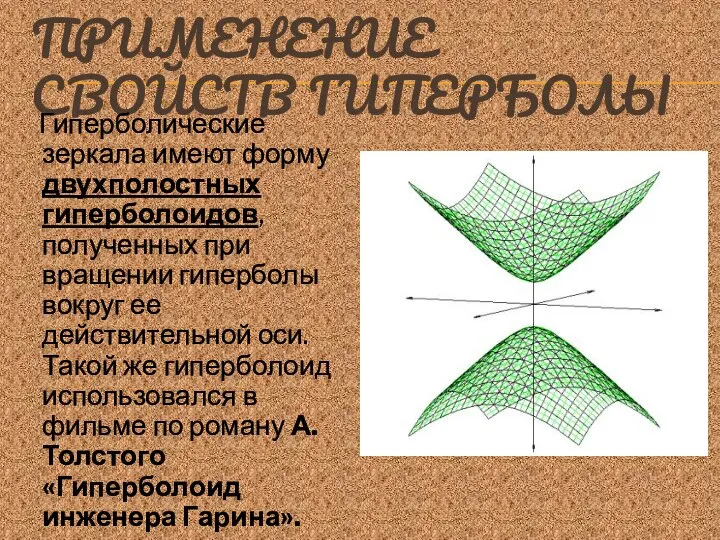
ПРИМЕНЕНИЕ СВОЙСТВ ГИПЕРБОЛЫ
Гиперболические зеркала имеют форму двухполостных гиперболоидов, полученных при вращении гиперболы вокруг ее действительной оси. Такой же гиперболоид использовался в фильме по роману А. Толстого «Гиперболоид инженера Гарина».

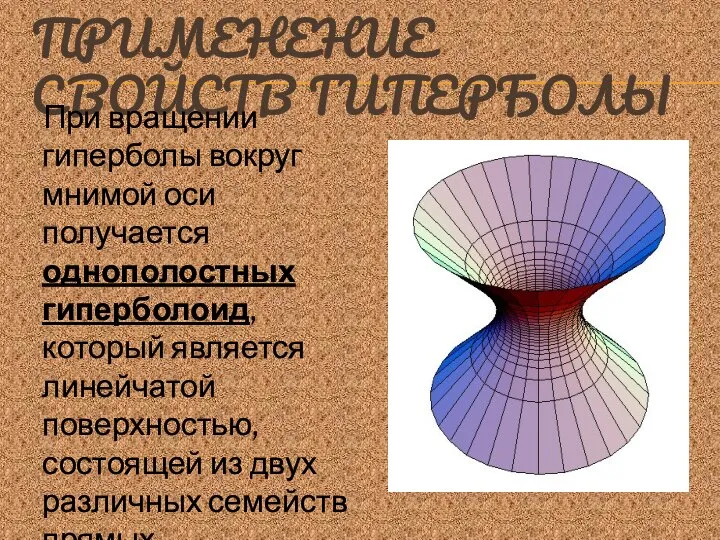
ПРИМЕНЕНИЕ СВОЙСТВ ГИПЕРБОЛЫ
При вращении гиперболы вокруг мнимой оси получается однополостных гиперболоид, который является линейчатой поверхностью, состоящей из двух различных семейств прямых.

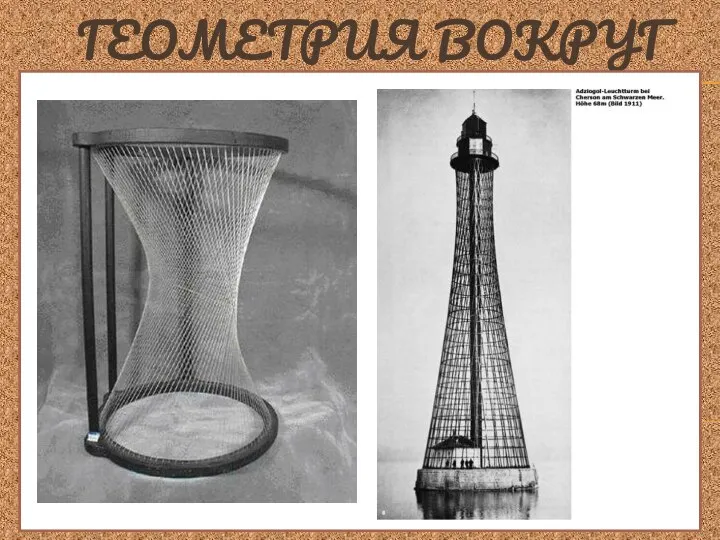
ПРИМЕНЕНИЕ СВОЙСТВ ГИПЕРБОЛЫ
Шу́ховская ба́шня (Ша́боловская ба́шня, Ра́дио-ба́шня) — уникальная гиперболоидная конструкция, выполненная в виде несущей стальной сетчатой оболочки. Расположена в Москве на улице Шаболовка. Построена в 1920—1922 годах. Памятник архитектуры. Автор проекта и руководитель строительства радио-башни — великий русский инженер, архитектор, и учёный, академик Владимир Григорьевич Шухов (1853-1939 гг.). Башня получила признание как одно из самых красивых и выдающихся достижений инженерной мысли в мире.

ПРИМЕНЕНИЕ СВОЙСТВ ГИПЕРБОЛЫ
Однополостный гиперболоид и гиперболический параболоид — дважды линейчатые поверхности, то есть через любую точку такой поверхности можно провести две пересекающиеся прямые, которые будут целиком принадлежать поверхности. Вдоль этих прямых и устанавливаются балки, образующие характерную решётку. Такая конструкция является жёсткой: если балки соединить шарнирно, гиперболоидная конструкция всё равно будет сохранять свою форму под действием внешних сил.
Для высоких сооружений основную опасность несёт ветровая нагрузка, а у решётчатой конструкции она невелика. Эти особенности делают гиперболоидные конструкции прочными, несмотря на невысокую материалоёмкость.

ГЕОМЕТРИЯ ВОКРУГ НАС
Гипербола является графиком различных кривых второго порядка. Даже такое простое уравнение, как ab=c, где с – константа, порождает график в виде гиперболы. Аналогичное уравнение описывает многие физические законы (например, закон Бойля и закон Ома).

КАК УВИДЕТЬ ГИПЕРБОЛУ?
Предлагаем дома провести
простой эксперимент, позволяющий «увидеть» кривую, описываемую зависимостью
ab=c,
который приведён в книге Мартина Гарднера
«От мозаик Пенроуза к надёжным шифрам»
в главе 15, посвящённой гиперболе.
Установить две стеклянные пластины в сосуд с подкрашенной водой так, чтобы с одной стороны они совмещались, а с другой – были разведены. Вставить между ними полоску картона, стянуть их резинками. Под действием капиллярных сил образуется гипербола.

ГИПЕРБОЛА ОТ СВЕЧИ
Гипербола в жизни встречается
гораздо реже, чем парабола или эллипс.
Наши предки наблюдали ветвь гиперболы на стене, когда подносили к ней горящую свечу в подсвечнике с круглым основанием.

ГИПЕРБОЛА В СВЕТЕ ЛАМПЫ
Изредка мы можем видеть полную гиперболу, если лампа с цилиндрическим или коническим абажуром отбрасывает тень на соседнюю стенку.

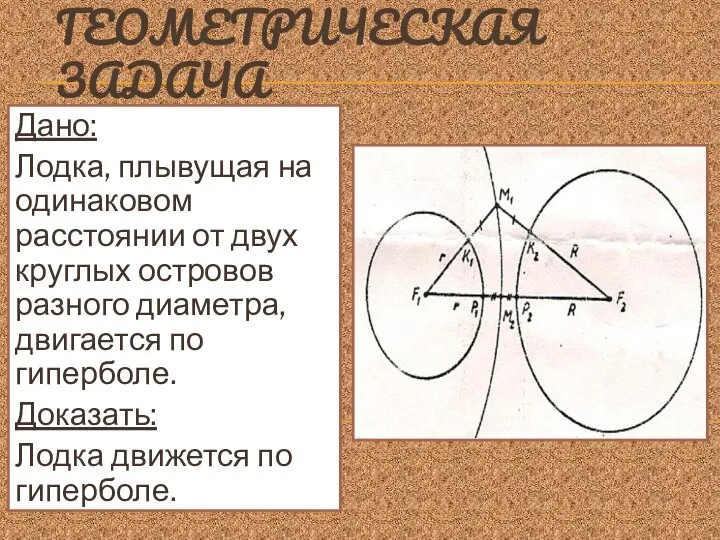
ГЕОМЕТРИЧЕСКАЯ ЗАДАЧА
Дано:
Лодка, плывущая на одинаковом расстоянии от двух круглых островов разного диаметра, двигается по гиперболе.
Доказать:
Лодка движется по гиперболе.

ДОКАЗАТЕЛЬСТВО
M1K1=M1K2;
M2P1=M2P2
M1F2-M1F1=R-r
M2F2-M2F1=R-r
(M1F1-M1F2)=(M2F2-M2F1)
Вывод: Линия движения есть геометрическое место точек М, разность расстояний от которых до F1 и F2 постоянна, значит, линия движения – ветвь гиперболы.

ГЕОМЕТРИЯ ВОКРУГ НАС

ГЕОМЕТРИЯ ВОКРУГ НАС