Содержание
- 2. Цель: Доказать, что можно измерить глубину озера, не используя специальных приборов, зная только теорему Пифагора. Ход
- 3. Мысли по поводу... Для нахождения расстояний, высот, глубины или других размеров реальных объектов не всегда можно
- 4. Делаю замеры. Однажды я был на рыбалке. Плавая по озеру на лодке, я захотел узнать его
- 5. Мои расчеты - глубина озера Подробнее Вывод формулы
- 6. Сравнение результатов. Определяя среднее арифметическое трех результатов, нахожу глубину озера Чередовое:
- 7. Вывод: Применяя теорему Пифагора, можно измерить глубину озера, не используя специальных измерительных приборов.
- 8. Используемая литература: Л.С. Атанасян, В.Ф. Бутузов и др.Геометрия:Учеб. Для 7-9 кл.общеобразоват.учреждений. – М.: Просвещение,2003. С.Б.Гашков Примени
- 10. Скачать презентацию







 Параллельное и последовательное соединения
Параллельное и последовательное соединения 1665470218901_Лекция Бернулли-1
1665470218901_Лекция Бернулли-1 Математический анализ. Производная и первообразная
Математический анализ. Производная и первообразная Доли. Математический диктант
Доли. Математический диктант Аксиома параллельных прямых
Аксиома параллельных прямых Внесение множителя под знак корня. Вынесение множителя из-под знака корня
Внесение множителя под знак корня. Вынесение множителя из-под знака корня Математика без границ. Конкурс
Математика без границ. Конкурс Координатная плоскость
Координатная плоскость Множественный регрессионный анализ
Множественный регрессионный анализ Игра Что? Где? Почему?
Игра Что? Где? Почему? Приемы быстрого счёта в математике
Приемы быстрого счёта в математике Второй признак равенства треугольников по стороне и двум прилежащим к ней углам
Второй признак равенства треугольников по стороне и двум прилежащим к ней углам Гистограммы. Представление статистических данных в графическом виде
Гистограммы. Представление статистических данных в графическом виде Природа России в цифрах и загадках
Природа России в цифрах и загадках Урок 14. Первый признак равенства треугольников
Урок 14. Первый признак равенства треугольников Прогрессия. Анзац
Прогрессия. Анзац Случаи вычитания 12 -
Случаи вычитания 12 - Движения. 9-й класс
Движения. 9-й класс Решение задач на тему Энергосбережение
Решение задач на тему Энергосбережение Решение уравнений и неравенств
Решение уравнений и неравенств Решение задач по теме Площадь параллелограмма, треугольника, трапеции
Решение задач по теме Площадь параллелограмма, треугольника, трапеции Действия с обыкновенными дробями. Подготовка к ОГЭ задания первой части 1, 3, 8
Действия с обыкновенными дробями. Подготовка к ОГЭ задания первой части 1, 3, 8 Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии Презентация на тему Умножение числа 2
Презентация на тему Умножение числа 2 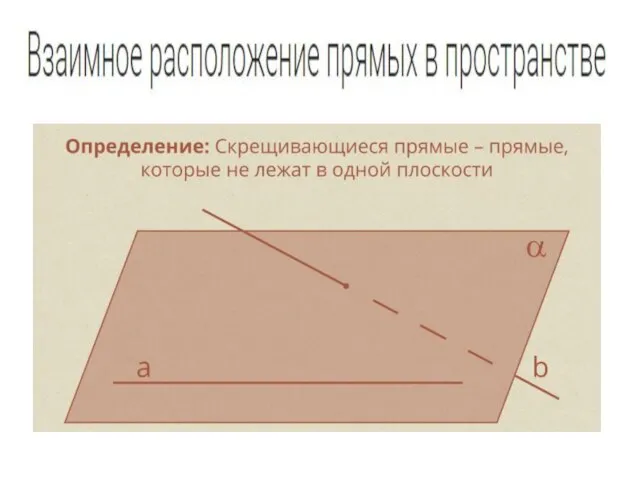 Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве Презентация на тему Решение задач с помощью квадратных уравнений
Презентация на тему Решение задач с помощью квадратных уравнений  Соотношения между сторонами и углами треугольника. Подготовка к контрольной работе
Соотношения между сторонами и углами треугольника. Подготовка к контрольной работе Углы, связанные с окружностью
Углы, связанные с окружностью