Содержание
- 2. Продолжите предложение. Продолжите предложение. Устная работа Продолжите предложение. 1. Окружность – это геометрическая фигура, состоящая 2.
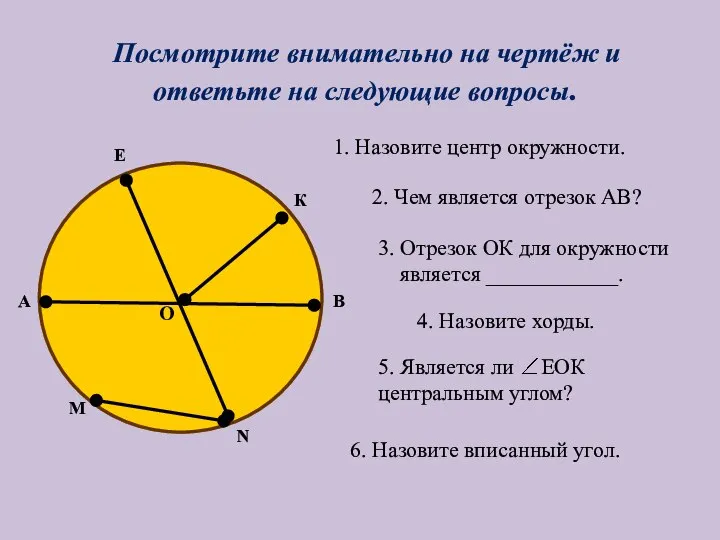
- 3. О М N А В Е К Посмотрите внимательно на чертёж и ответьте на следующие вопросы.
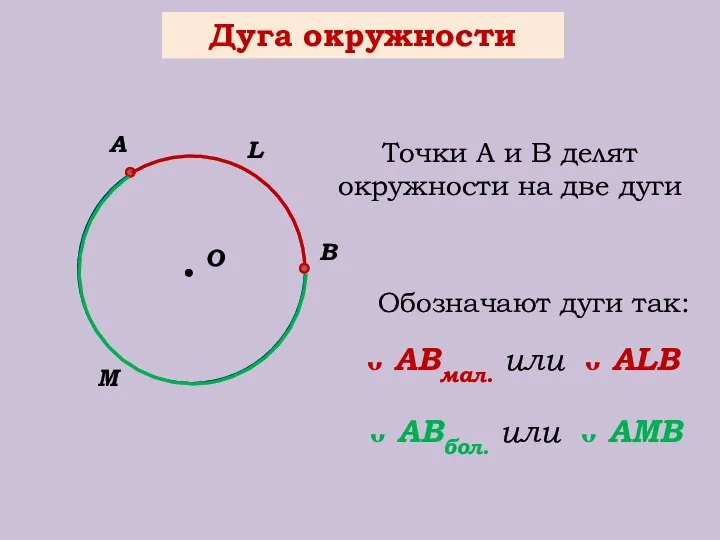
- 4. Дуга окружности О В А М L Точки А и В делят окружности на две дуги
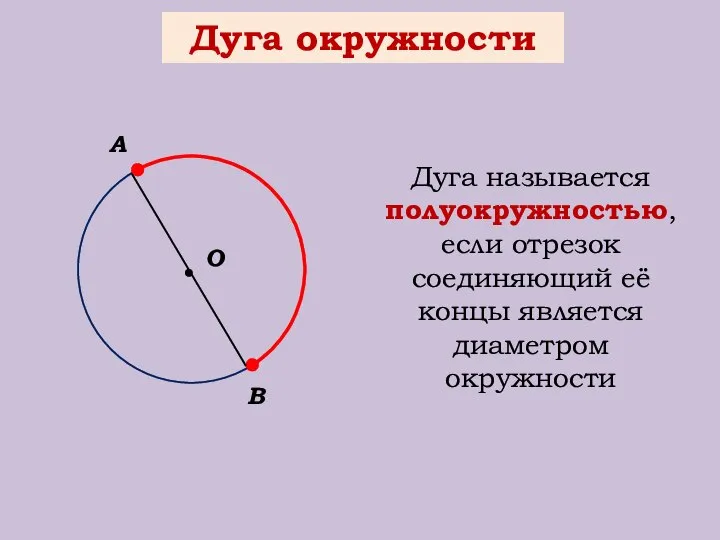
- 5. Дуга окружности О В А Дуга называется полуокружностью, если отрезок соединяющий её концы является диаметром окружности
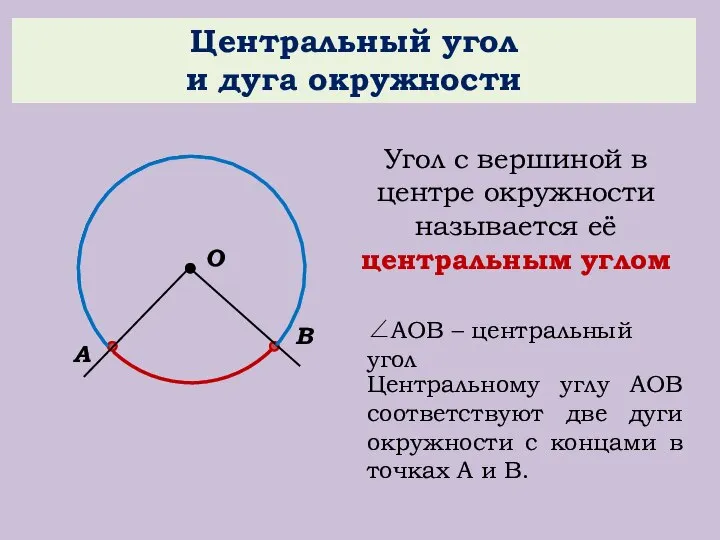
- 6. Центральный угол и дуга окружности О В А Угол с вершиной в центре окружности называется её
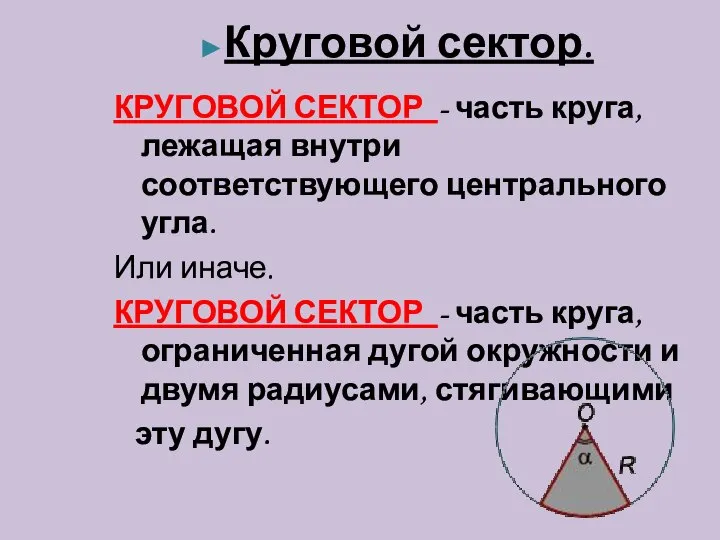
- 7. ►Круговой сектор. КРУГОВОЙ СЕКТОР - часть круга, лежащая внутри соответствующего центрального угла. Или иначе. КРУГОВОЙ СЕКТОР
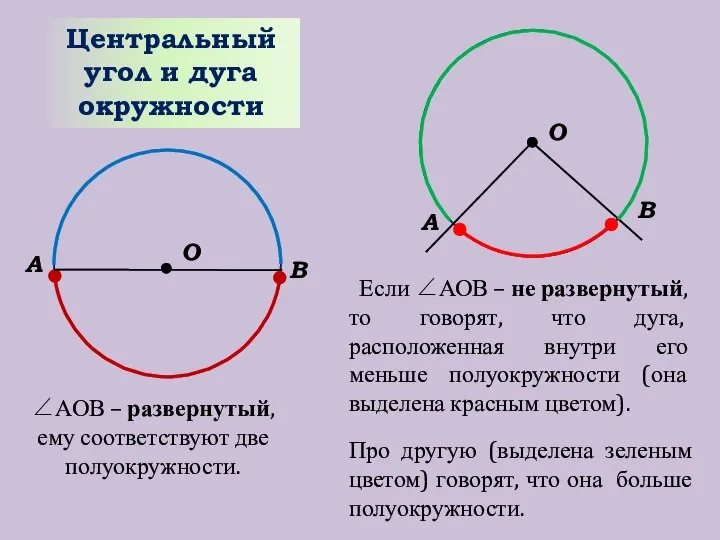
- 8. О В А Центральный угол и дуга окружности ∠АОВ – развернутый, ему соответствуют две полуокружности. О
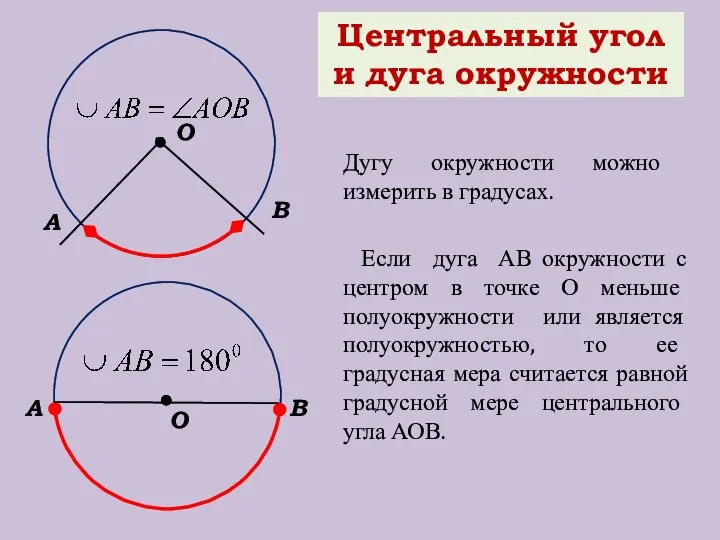
- 9. Центральный угол и дуга окружности О В А Если дуга АВ окружности с центром в точке
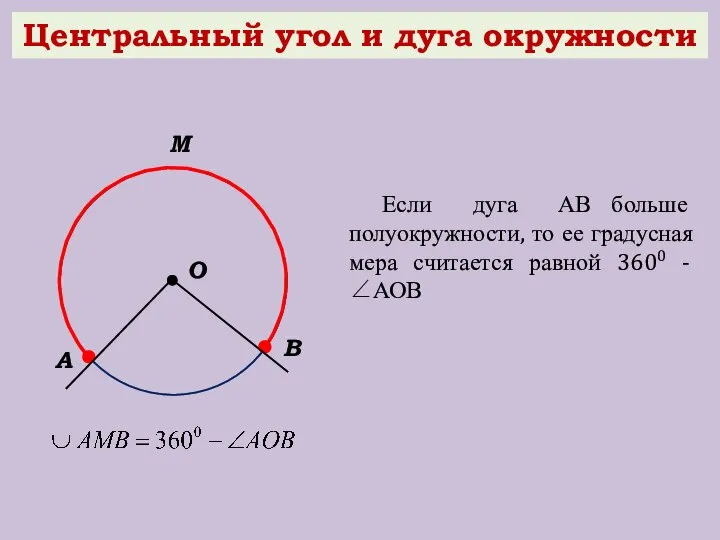
- 10. Центральный угол и дуга окружности О В А Если дуга АВ больше полуокружности, то ее градусная
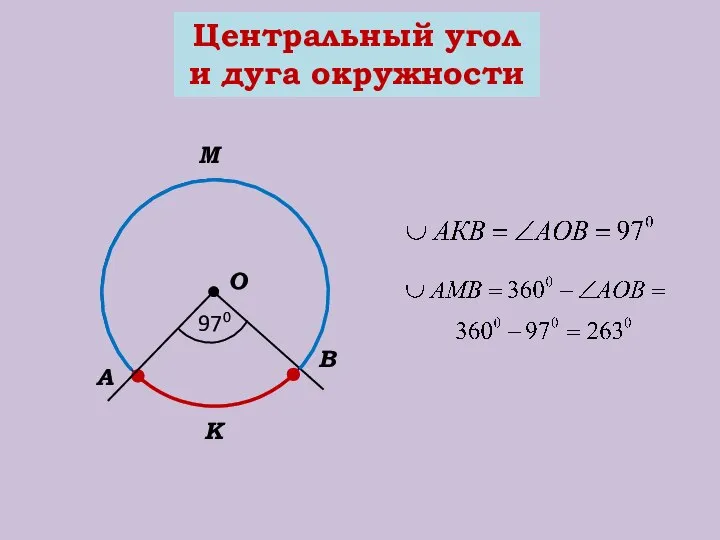
- 11. Центральный угол и дуга окружности О В А 970 М К
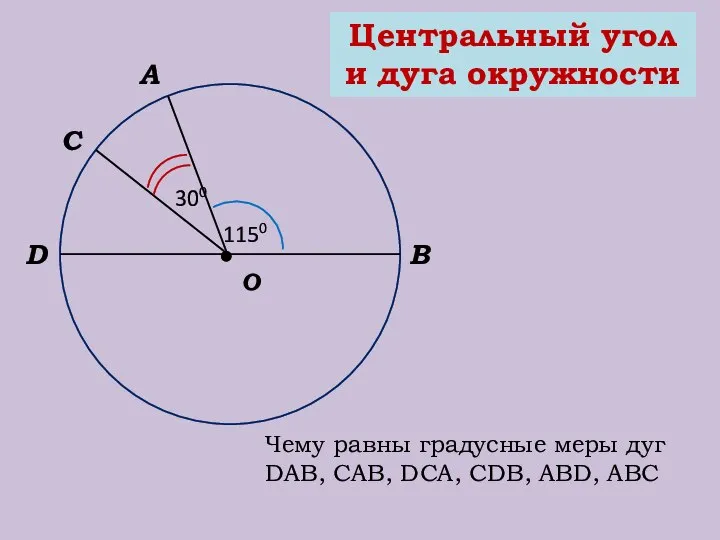
- 12. Центральный угол и дуга окружности О В А 300 С D 1150 Чему равны градусные меры
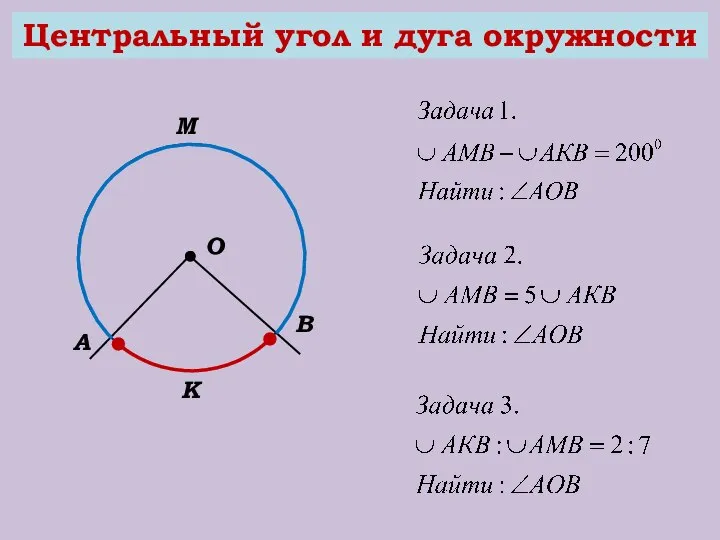
- 13. Центральный угол и дуга окружности О В А М К
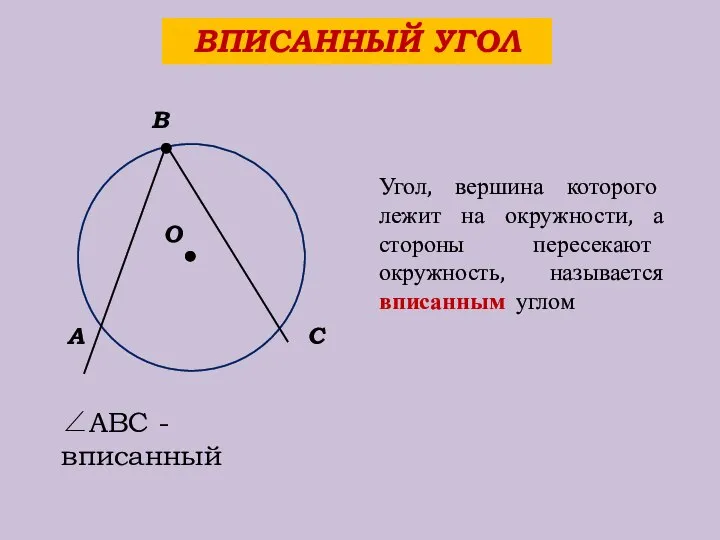
- 14. ВПИСАННЫЙ УГОЛ О В А С Угол, вершина которого лежит на окружности, а стороны пересекают окружность,
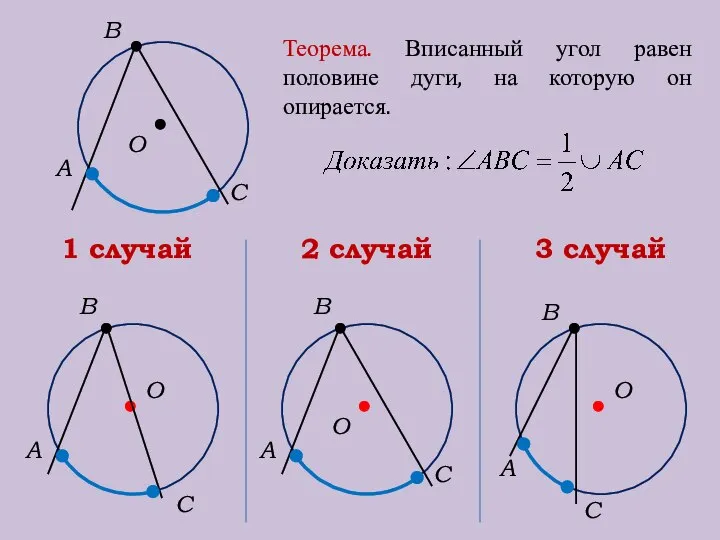
- 15. О В А С Теорема. Вписанный угол равен половине дуги, на которую он опирается. О А
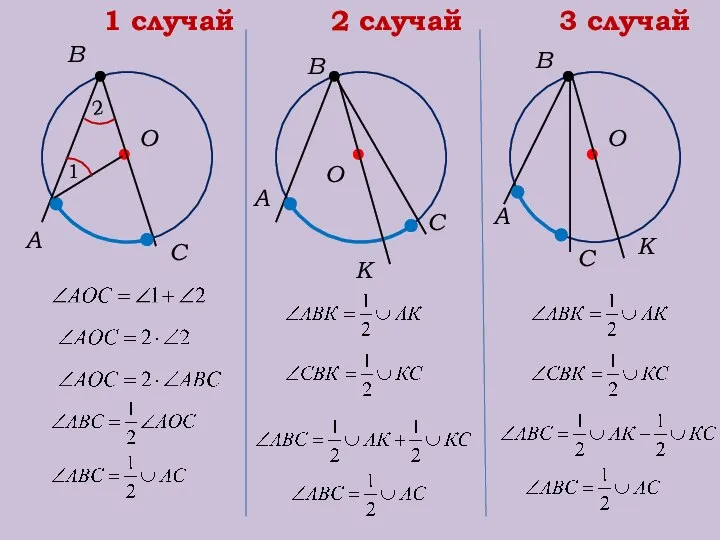
- 16. О А С О А С О А С В В В 1 случай 2 случай
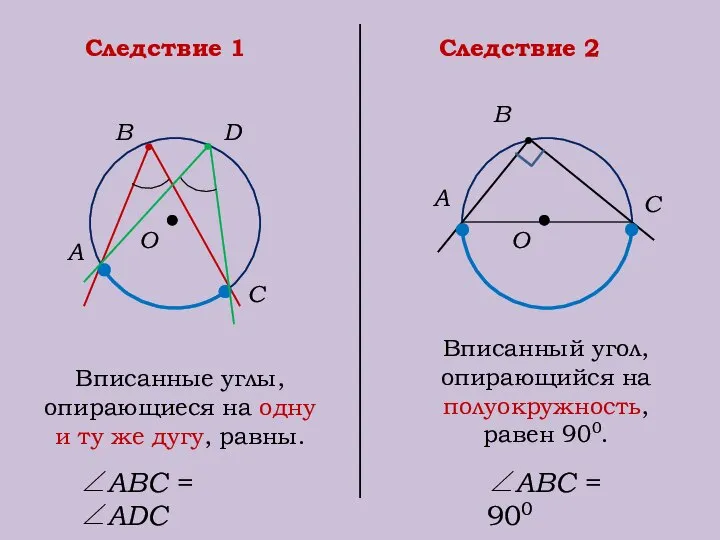
- 17. О В А С О А С Следствие 1 Следствие 2 В D Вписанные углы, опирающиеся
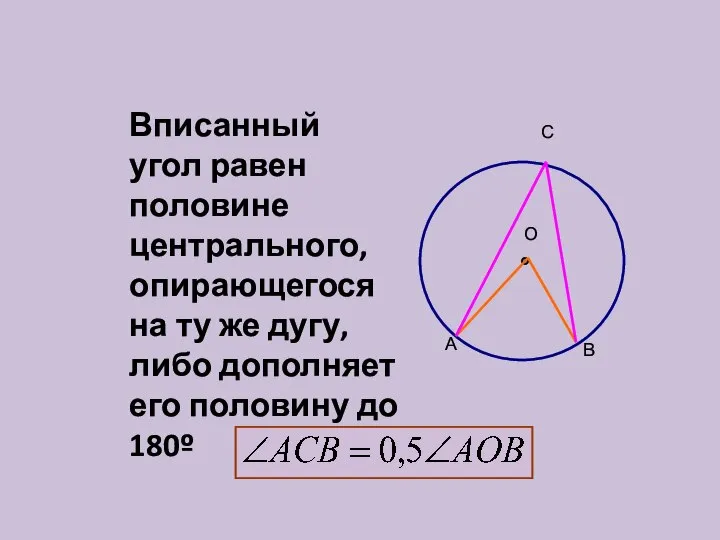
- 18. Вписанный угол равен половине центрального, опирающегося на ту же дугу, либо дополняет его половину до 180º
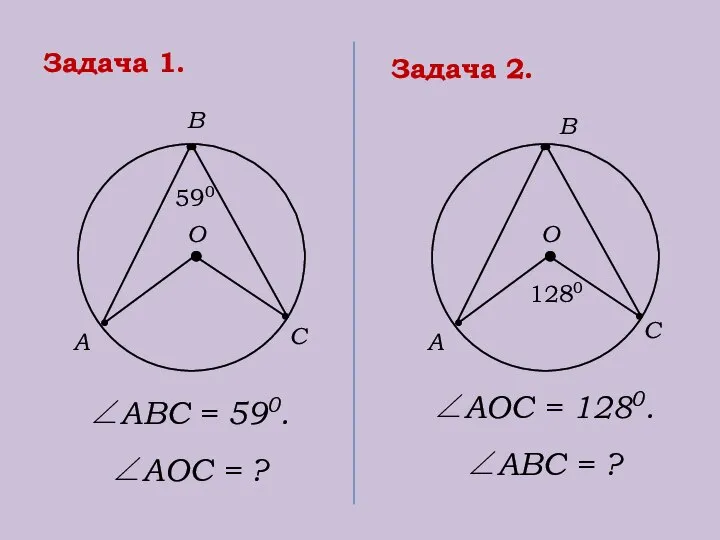
- 19. Задача 1. А О В С 590 ∠АВС = 590. ∠АОС = ? Задача 2. А
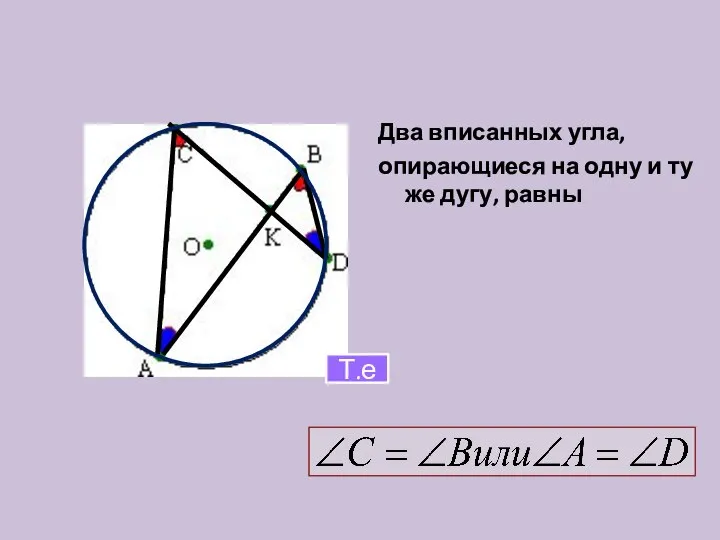
- 20. Два вписанных угла, опирающиеся на одну и ту же дугу, равны Т.е
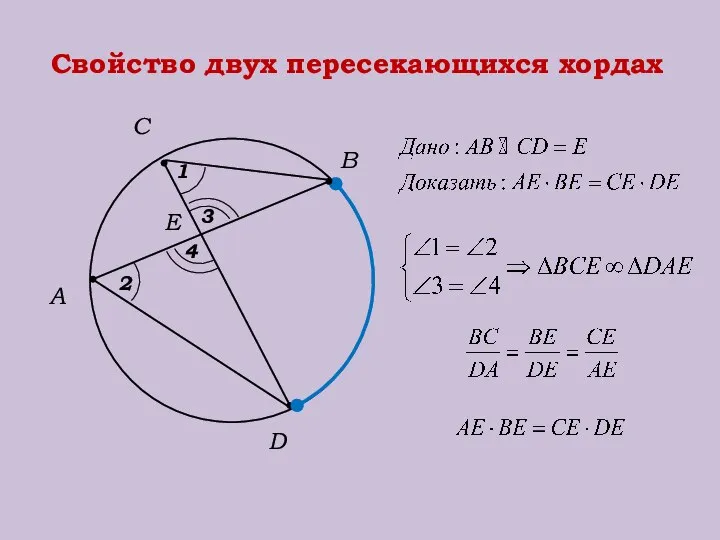
- 21. Свойство двух пересекающихся хордах Е А С В D 1 2 3 4
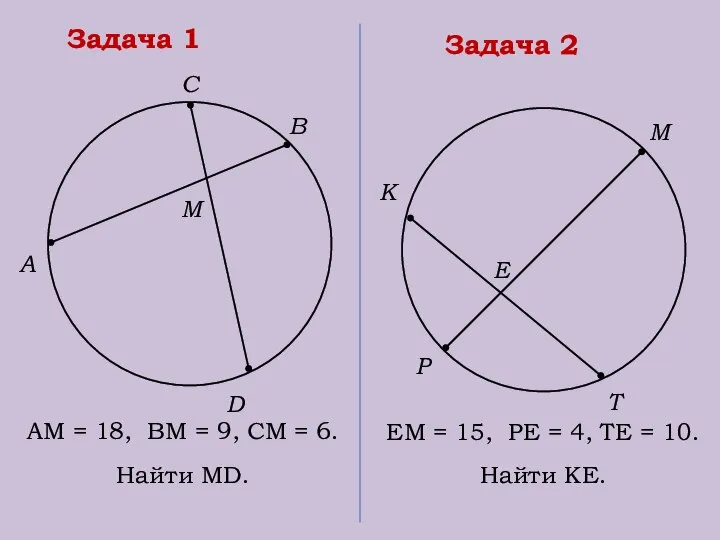
- 22. Задача 1 М А С В D АМ = 18, ВМ = 9, СМ = 6.
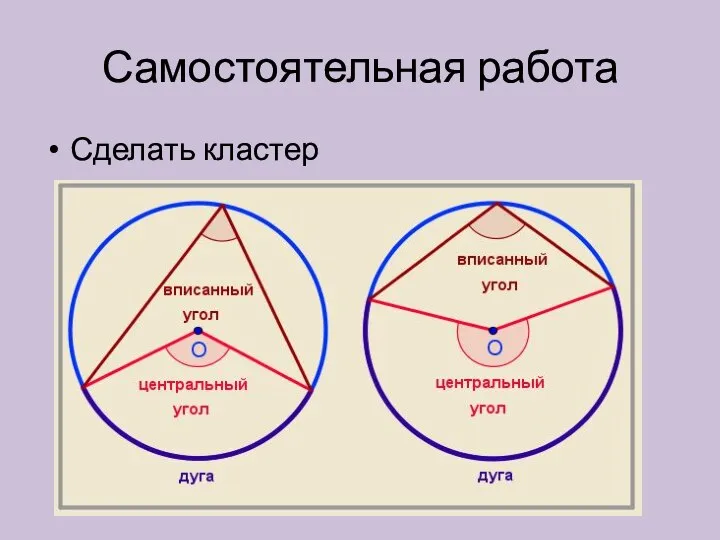
- 23. Самостоятельная работа Сделать кластер
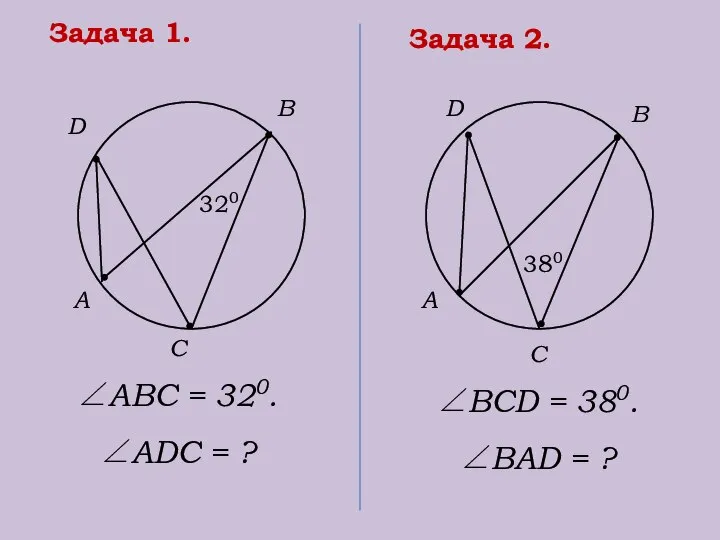
- 24. Задача 1. А D В С 320 ∠АВС = 320. ∠АDС = ? Задача 2. А
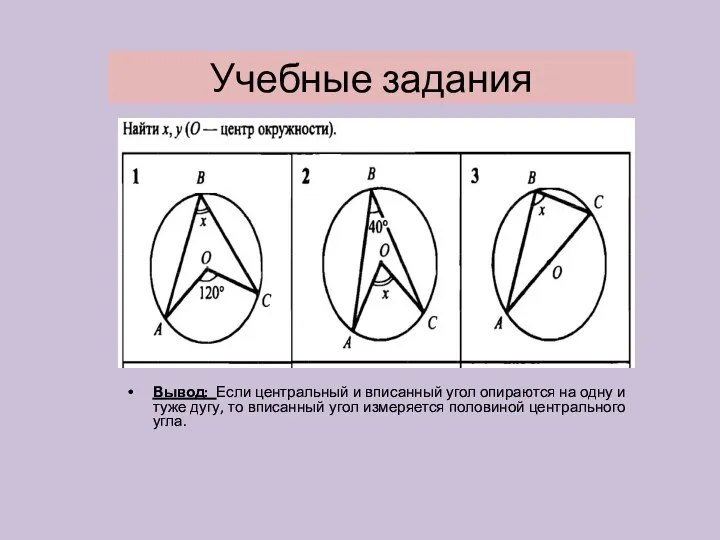
- 25. Учебные задания Вывод: Если центральный и вписанный угол опираются на одну и туже дугу, то вписанный
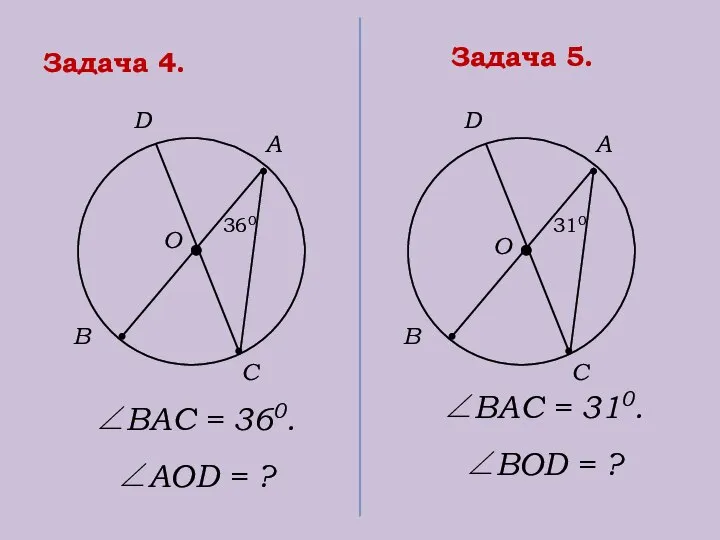
- 26. Задача 4. А О В С 360 ∠BAC = 360. ∠АОD = ? Задача 5. ∠BAC
- 28. Скачать презентацию

 Презентация на тему Признаки равенства треугольников
Презентация на тему Признаки равенства треугольников  Сравниваем выражения. 2 класс
Сравниваем выражения. 2 класс Применение производной к построению графиков функции
Применение производной к построению графиков функции Подготовка к ЕГЭ
Подготовка к ЕГЭ Презентация на тему ЛОГАРИФМ ЧИСЛА
Презентация на тему ЛОГАРИФМ ЧИСЛА  Разработка обучающей программы по нахождению элементов треугольника
Разработка обучающей программы по нахождению элементов треугольника Повторение. Свойства умножения. Свойства деления
Повторение. Свойства умножения. Свойства деления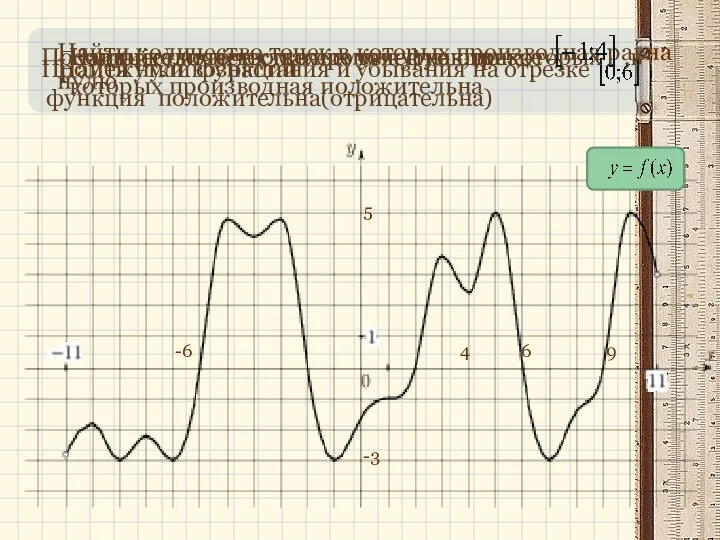 Алгоритм нахождения интервалов выпуклости и точек перегиба
Алгоритм нахождения интервалов выпуклости и точек перегиба Все действия с рациональными дробями. Подготовка к контрольной работе
Все действия с рациональными дробями. Подготовка к контрольной работе Обыкновенные дифференциальные уравнения первого порядка. Классификация и решение
Обыкновенные дифференциальные уравнения первого порядка. Классификация и решение 2.1._-_
2.1._-_ Письменное умножение трехзначных чисел (3 класс)
Письменное умножение трехзначных чисел (3 класс) Презентация на тему Математика вокруг нас. Математика в строительстве
Презентация на тему Математика вокруг нас. Математика в строительстве  Устный счёт. 1 класс
Устный счёт. 1 класс Модуль Начертательная геометрия. Тема 6
Модуль Начертательная геометрия. Тема 6 Метод координат на плоскости
Метод координат на плоскости Деление и обобщение понятий. Круги Эйлера-Венна.
Деление и обобщение понятий. Круги Эйлера-Венна. Делители и кратные. 8.09.12 Классная работа.
Делители и кратные. 8.09.12 Классная работа. Сравнение групп предметов
Сравнение групп предметов Применение вычислительных методов в теории приближений непрерывных функций
Применение вычислительных методов в теории приближений непрерывных функций Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Конус – тело вращения
Конус – тело вращения Это забавные животные. Занимательные задачи
Это забавные животные. Занимательные задачи Длина окружности
Длина окружности 3.7. Непрерывность функции
3.7. Непрерывность функции Признаки равенства треугольников
Признаки равенства треугольников Прямая Эйлера
Прямая Эйлера Тестирование
Тестирование