Содержание
- 2. Цель работы: выявить наиболее рациональное решение, быстро приводящее к ответу. Задача: - рассмотреть теорию методов решения
- 3. История возникновения Задачи на уравнения с параметром встречались уже в астрономическом трактате «Ариабхатиам», составленном в 499
- 4. Автор насчитывает 6 видов уравнений, выражая их следующим образом: 1) «Квадраты равны корням», т. е. αx2
- 5. Теорема Виетта (α + b)x – x2 = αb, Т. е. x2 - (α –b)x +
- 6. Основные понятия Параметр- независимая переменная, значение которой считается фиксированным или произвольным числом, или числом, принадлежащим заданному
- 7. Методы решения уравнений с параметрами 1.Аналитический метод 2.Графический метод 3.Алгебраический метод 4.Метод симметрии 5.Решение с помощью
- 8. Небольшая история возникновения этого метода. Исследование общих зависимостей началось еще в 14 веке. Французский учёный Николай
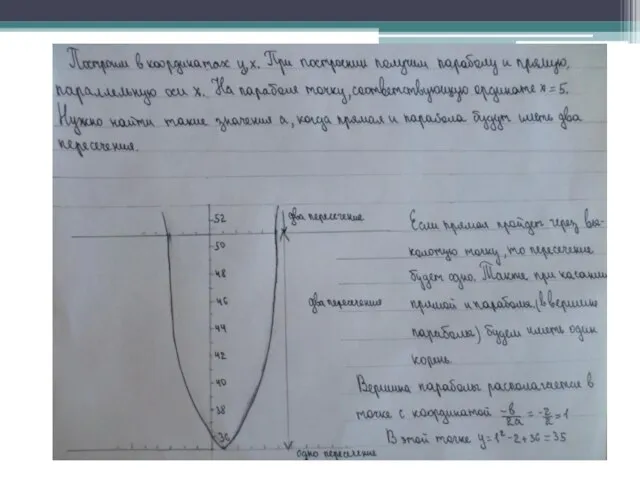
- 9. Графический метод График функции- множество точек, у которых с абсциссы являются допустимыми значениями аргумента х, а
- 10. Виды уравнений с параметрами Линейное ( ax=b) Квадратное(ax^2+bx+c=0) Логарифмическое Тригонометрическое
- 11. Решение логарифмического уравнения с параматером
- 14. Заключение Таким образом, графический способ определения числа корней уравнения зависимости от входящего в него параметра, является
- 15. Список использованной литературы: 1. Справочник по математике. Автор Гусев В.А 2. Окунев А.А « Графическое решение
- 17. Скачать презентацию













 Презентация на тему Объем пирамиды
Презентация на тему Объем пирамиды  От перестановки множителей произведение не изменяется
От перестановки множителей произведение не изменяется Презентация на тему Платоновы тела Правильные выпуклые многогранники 10 класс
Презентация на тему Платоновы тела Правильные выпуклые многогранники 10 класс  preobrazovanie
preobrazovanie Третий признак равенства треугольников
Третий признак равенства треугольников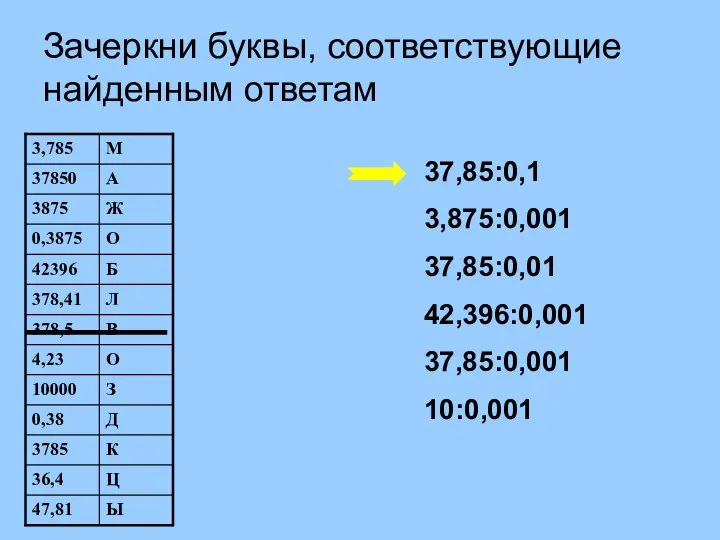 Устная работа (1). Зачеркни буквы, соответствующие найденным ответам
Устная работа (1). Зачеркни буквы, соответствующие найденным ответам Уравнение касательной
Уравнение касательной Теорема Пифагора
Теорема Пифагора Презентация на тему Порядок выполнения действий в выражениях со скобками
Презентация на тему Порядок выполнения действий в выражениях со скобками  Презентация на тему Округление натуральных чисел (5 класс)
Презентация на тему Округление натуральных чисел (5 класс)  Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Неисключенные остатки систематической погрешности. Статистическая обработка однократных наблюдений. Случайные погрешности
Неисключенные остатки систематической погрешности. Статистическая обработка однократных наблюдений. Случайные погрешности Геометрическое место точек. 7 класс
Геометрическое место точек. 7 класс Сокращенное умножение многочленов
Сокращенное умножение многочленов История математики в лицах великих учёных
История математики в лицах великих учёных Страничка для любознательных - задания творческого и поискового характера
Страничка для любознательных - задания творческого и поискового характера Эвристические приемы. Алгебра 8 класс
Эвристические приемы. Алгебра 8 класс Число 10
Число 10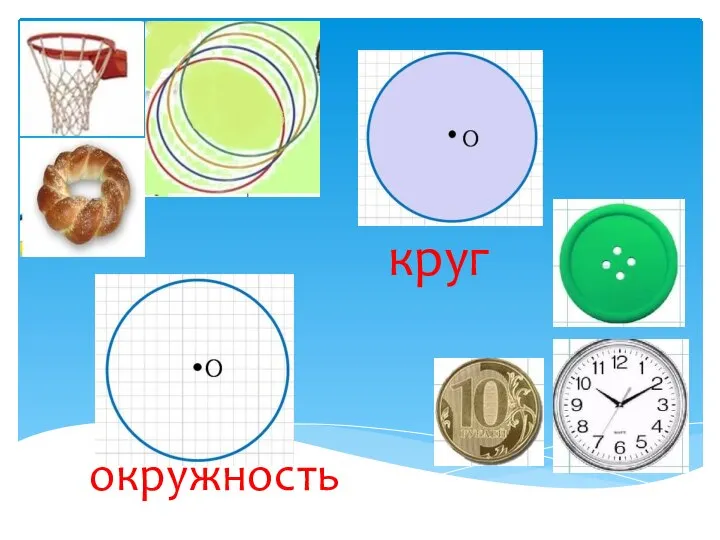 Круг, окружность
Круг, окружность Уравнение с параметром
Уравнение с параметром Взаимное расположение двух прямых в пространстве
Взаимное расположение двух прямых в пространстве Презентация на тему Решение комбинаторных задач и задач по теории вероятности
Презентация на тему Решение комбинаторных задач и задач по теории вероятности  Численные методы решения дифференциальных уравнений
Численные методы решения дифференциальных уравнений Задачи на кратное сравнение (закрепление)
Задачи на кратное сравнение (закрепление) Признаки параллельности прямых
Признаки параллельности прямых Тренировочные задания (графическое представление данных)
Тренировочные задания (графическое представление данных) Теория Пределов
Теория Пределов Стереометрия. Школьный курс
Стереометрия. Школьный курс