Графы и их применение при решении задач

Содержание
Что такое граф
Свойства графа
История возникновения графов
Задача о Кенигсбергских мостах
Применение графов
Выводы

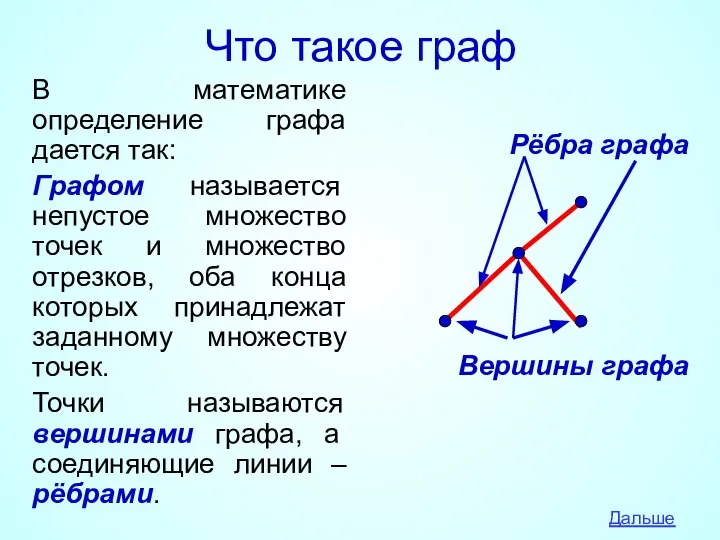
Что такое граф
В математике определение графа дается так:
Графом называется непустое множество точек и множество отрезков, оба конца которых принадлежат заданному множеству точек.
Точки называются вершинами графа, а соединяющие линии – рёбрами.
Рёбра графа
Вершины графа
Дальше

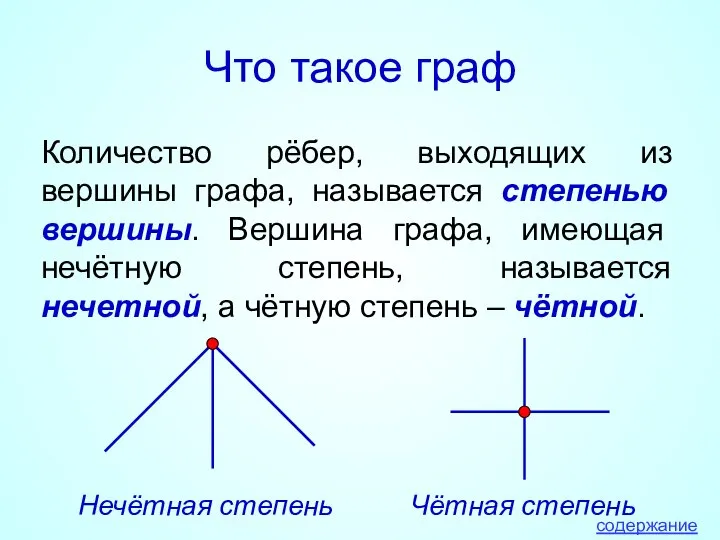
Что такое граф
Количество рёбер, выходящих из вершины графа, называется степенью вершины. Вершина графа, имеющая нечётную степень, называется нечетной, а чётную степень – чётной.
Нечётная степень
Чётная степень
содержание

Свойства графов
В графе сумма степеней всех его вершин – число чётное, равное удвоенному числу рёбер графа.
Число нечётных вершин любого графа чётно.
Во всяком графе с n вершинами, где n≥2, всегда найдутся две вершины с одинаковыми степенями.

Свойства графов
Если в графе с n вершинами (n>2) в точности две вершины имеют одинаковую степень, то в этом графе всегда найдётся либо в точности одна вершина степени 0, либо в точности одна вершина степени n-1.
Если полный граф имеет n вершин, то количество рёбер будет равно n(n-1)/2.

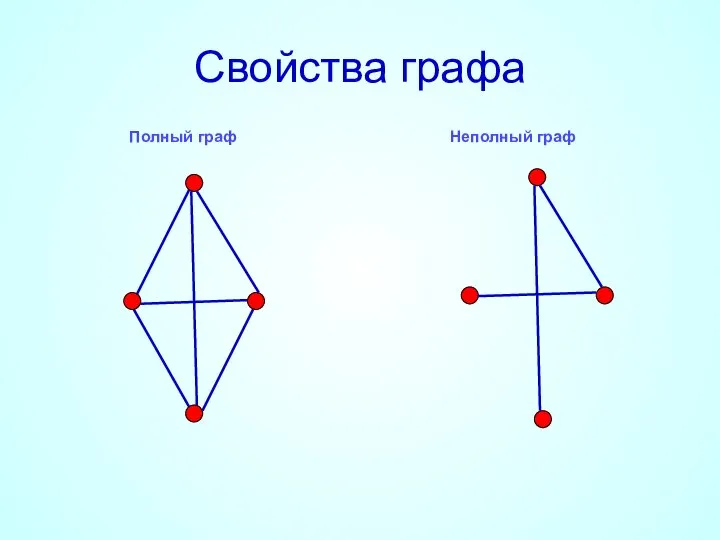
Свойства графа
Полный граф Неполный граф

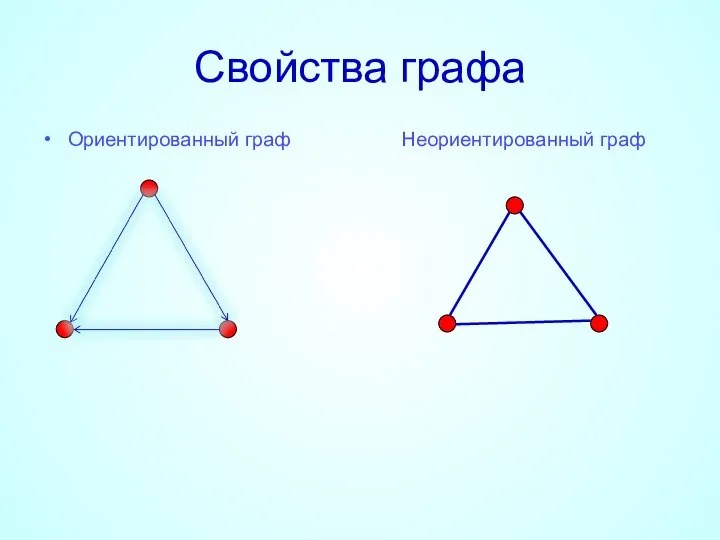
Свойства графа
Ориентированный граф Неориентированный граф

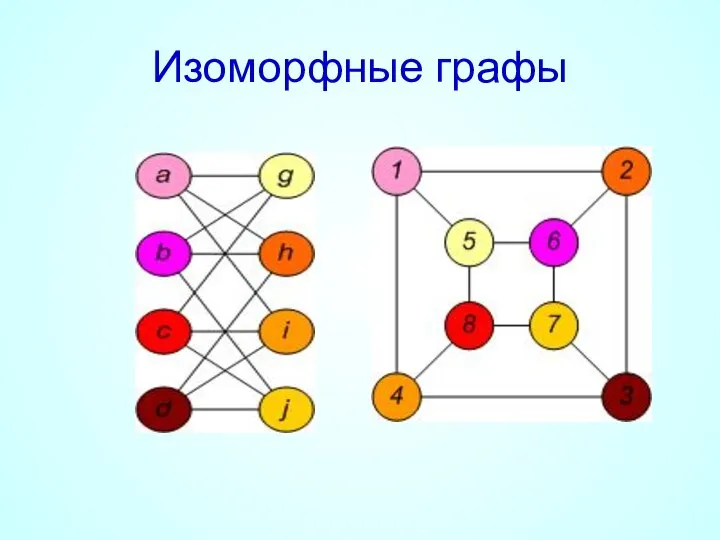
Изоморфные графы

История возникновения графов
Термин "граф" впервые появился в книге венгерского математика Д. Кенига в 1936 г., хотя начальные важнейшие теоремы о графах восходят к Л. Эйлеру.
Дальше

История возникновения графов
Основы теории графов как математической науки заложил в 1736 г. Леонард Эйлер, рассматривая задачу о кенигсбергских мостах. Сегодня эта задача стала классической.
содержание

Задача о Кенигсбергских мостах
Бывший Кенигсберг (ныне Калининград) расположен на реке Прегель. В пределах города река омывает два острова. С берегов на острова были перекинуты мосты. Старые мосты не сохранились, но осталась карта города, где они изображены.
Дальше

Задача о Кенигсбергских мостах
Среди жителей Кенигсберга была распространена следующая задача: можно ли пройти по всем мостам и вернуться в начальный пункт, побывав на каждом мосту только один раз?
Дальше

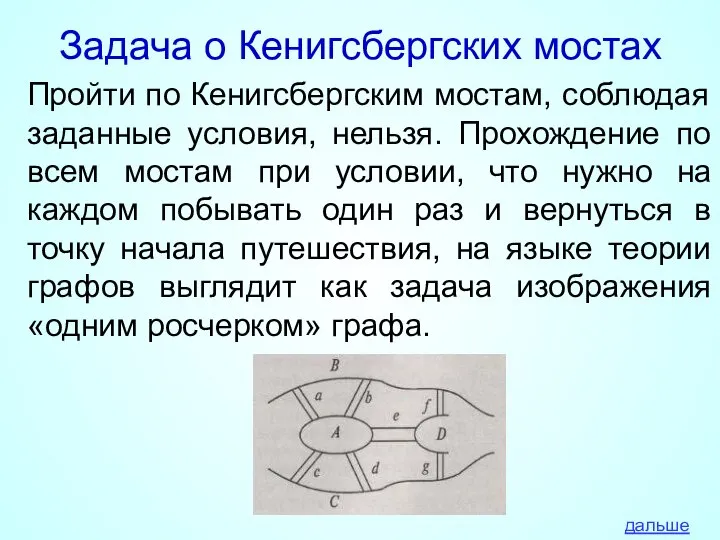
Задача о Кенигсбергских мостах
Пройти по Кенигсбергским мостам, соблюдая заданные условия, нельзя. Прохождение по всем мостам при условии, что нужно на каждом побывать один раз и вернуться в точку начала путешествия, на языке теории графов выглядит как задача изображения «одним росчерком» графа.
дальше

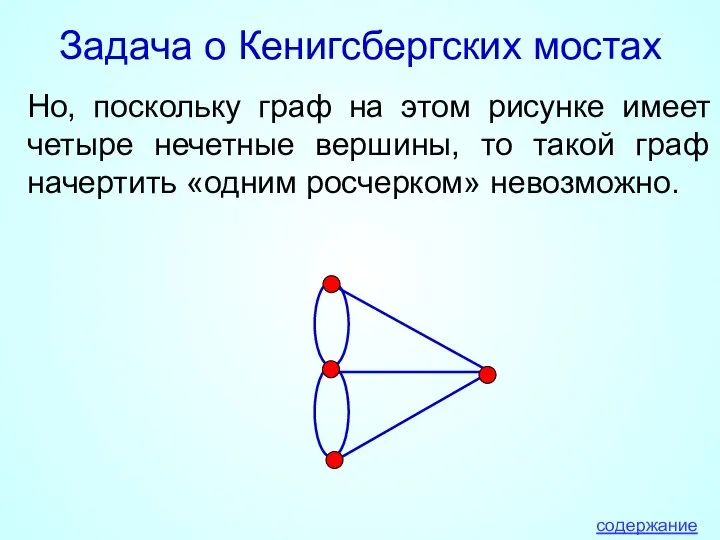
Задача о Кенигсбергских мостах
Но, поскольку граф на этом рисунке имеет четыре нечетные вершины, то такой граф начертить «одним росчерком» невозможно.
содержание

Эйлеров граф
Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым.
Решая задачу о кенигсбергских мостах, Эйлер сформулировал свойства графа:
Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин.
Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
дальше

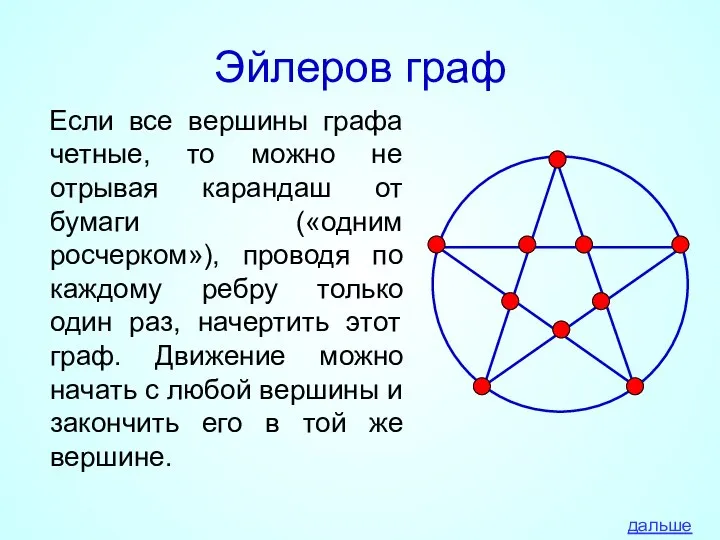
Эйлеров граф
Если все вершины графа четные, то можно не отрывая карандаш от бумаги («одним росчерком»), проводя по каждому ребру только один раз, начертить этот граф. Движение можно начать с любой вершины и закончить его в той же вершине.
дальше

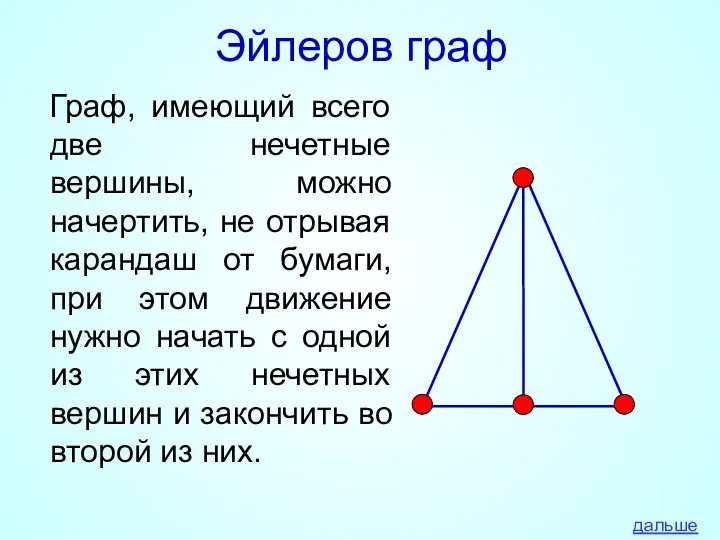
Эйлеров граф
Граф, имеющий всего две нечетные вершины, можно начертить, не отрывая карандаш от бумаги, при этом движение нужно начать с одной из этих нечетных вершин и закончить во второй из них.
дальше

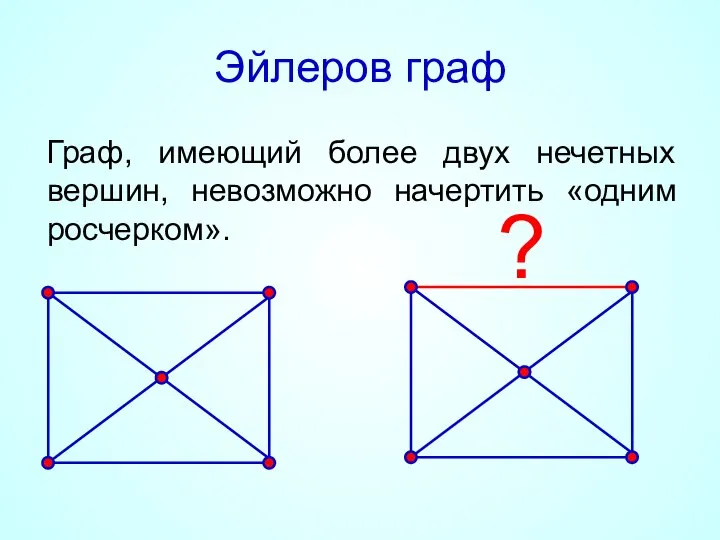
Эйлеров граф
Граф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком».
?

Применение графов
С помощью графов упрощается решение математических задач, головоломок, задач на смекалку.
дальше

Применение графов
Задача:
Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано?
дальше

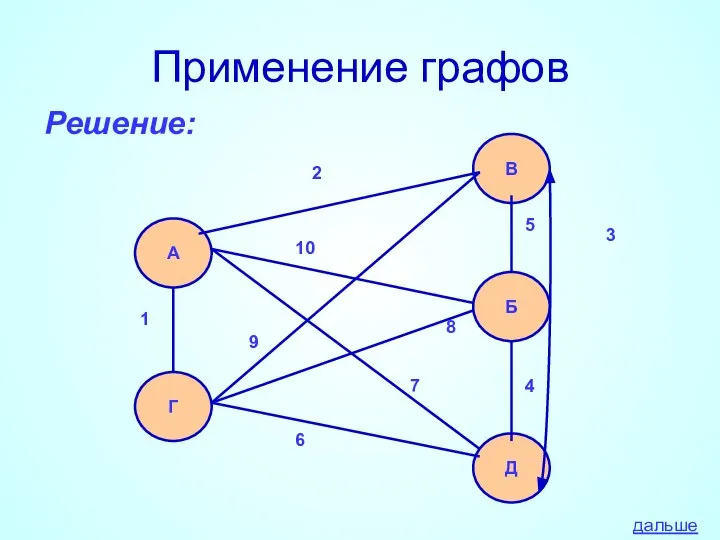
Применение графов
Решение:
А
Г
В
Б
Д
1
2
3
4
5
6
7
8
9
10
дальше

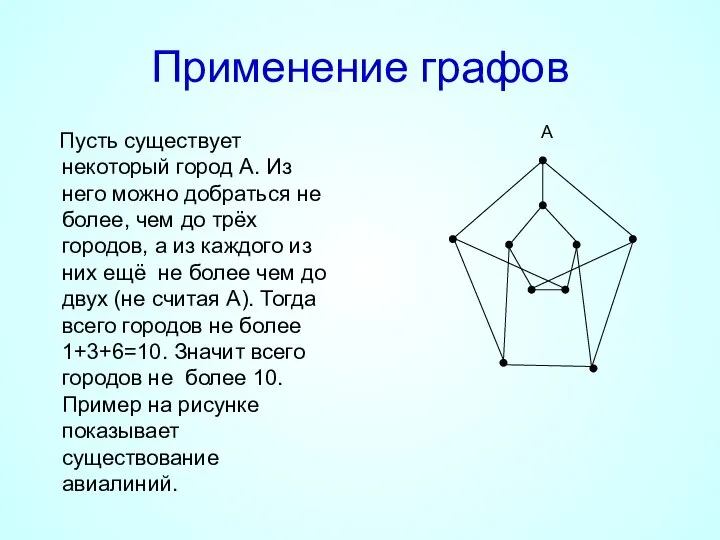
Применение графов
В государстве система авиалиний устроена таким образом, что любой город соединён авиалиниями не более чем с тремя другими, и из любого города в любой другой можно проехать, сделав не более одной пересадки. Какое максимальное число городов может быть в этом государстве?

Применение графов
Пусть существует некоторый город А. Из него можно добраться не более, чем до трёх городов, а из каждого из них ещё не более чем до двух (не считая А). Тогда всего городов не более 1+3+6=10. Значит всего городов не более 10. Пример на рисунке показывает существование авиалиний.
А

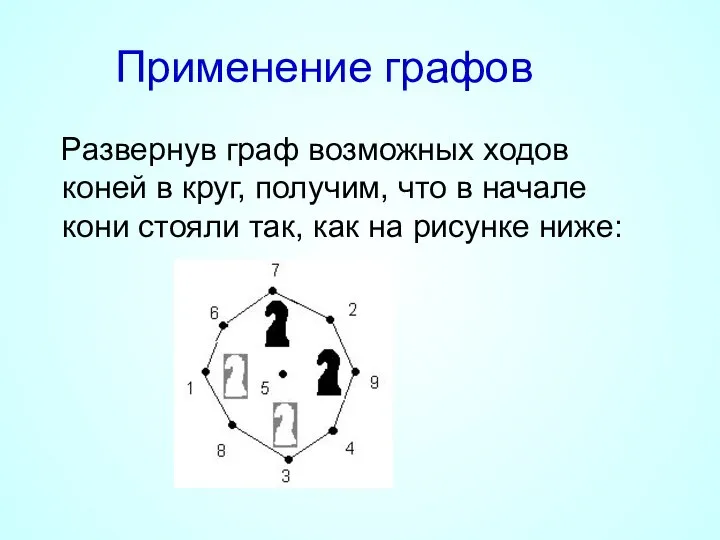
Применение графов
Имеется шахматная доска 3x3, в верхних двух углах стоят два чёрных коня, в нижних – два белых (рисунок ниже). За 16 ходов поставьте белых коней на место чёрных, а чёрных на место белых и докажите, что за меньшее число ходов это сделать невозможно.

Применение графов
Развернув граф возможных ходов коней в круг, получим, что в начале кони стояли так, как на рисунке ниже: