Содержание
- 2. Личностные цели 1.Научиться анализировать и делать выводы путем своих рассуждений. 2. Уметь точно и грамотно излагать
- 3. В конце урока предстоит оценить результат своей деятельности. За каждый правильный ответ на полях тетрадки ставьте
- 4. Вывод 5
- 5. Уравнение, в котором хотя бы один член содержит неизвестное под знаком корня, называется иррациональным. Уравнение, в
- 6. 5
- 7. Вывод 10
- 8. Возвести обе части уравнения в степень, равную степени корня. Решить полученное уравнение. 3. Выполнить проверку. 2
- 9. Метод «пристального взгляда» 2
- 10. 1. Составьте из представленного уравнения другие, ему равносильные уравнения. 10 Метод уединения радикала
- 11. Решите уравнение Ответ: -5; 4.
- 12. 1. Возвести обе части в квадрат, используя формулы квадрата разности или суммы. 2. Упростить левую и
- 13. Предлагаю побыть экспертами. Перед вами работы учащихся. Вам необходимо найти ошибки, если они есть. 1. 2.
- 14. 3.
- 16. Домашнее задание: №362 (б), № 363 (б), №364(б)
- 18. Скачать презентацию















 Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника Презентация на тему Параллельность прямых и плоскостей (10 класс)
Презентация на тему Параллельность прямых и плоскостей (10 класс)  Равносильность формул
Равносильность формул Методы решения систем линейных уравнений: метод сложения
Методы решения систем линейных уравнений: метод сложения Применение распределительного свойства умножения
Применение распределительного свойства умножения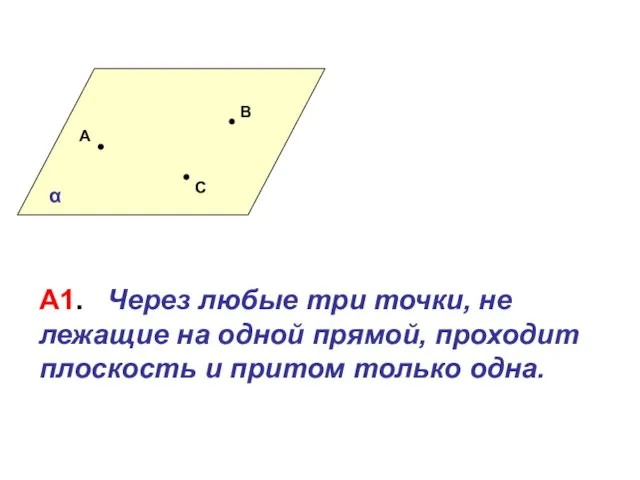 Плоскости
Плоскости Параллельные и перпендикулярные прямые
Параллельные и перпендикулярные прямые Устный счёт. Транспорт
Устный счёт. Транспорт Неопределенный интеграл. Способы вычисления
Неопределенный интеграл. Способы вычисления Презентация на тему Деление многозначных чисел
Презентация на тему Деление многозначных чисел  Понятие процента
Понятие процента Умножение пяти, на 5 и соответствующие случаи деления. Математика 3 класс. Учителя начальных классов Лаишевской специальной школ
Умножение пяти, на 5 и соответствующие случаи деления. Математика 3 класс. Учителя начальных классов Лаишевской специальной школ Математика в профессии сварщика
Математика в профессии сварщика Производные некоторых элементарных функций
Производные некоторых элементарных функций Форма прямоугольника
Форма прямоугольника Параллельность в пространстве
Параллельность в пространстве Анализ и изображение пространственных фигур
Анализ и изображение пространственных фигур Ромб, квадрат. Ответы на вопросы
Ромб, квадрат. Ответы на вопросы Геометрические фигуры (интерактивная игра)
Геометрические фигуры (интерактивная игра) Параллелограмм. Свойства параллелограмма. Трапеция
Параллелограмм. Свойства параллелограмма. Трапеция Объем наклонной призмы. Теорема
Объем наклонной призмы. Теорема Изображение пространственных фигур на плоскости
Изображение пространственных фигур на плоскости Решение уравнений третьей степени при подготовке к ЕГЭ
Решение уравнений третьей степени при подготовке к ЕГЭ Знаки тригонометрических функций. Формулы сложения
Знаки тригонометрических функций. Формулы сложения Карточки по математике. Состав числа
Карточки по математике. Состав числа Усеченная пирамида
Усеченная пирамида Лабораторная работа №1. Вычисление прямоугольных координат по геодезическим
Лабораторная работа №1. Вычисление прямоугольных координат по геодезическим Задачи на кратное сравнение
Задачи на кратное сравнение