Переменные величины и их свойства

Под величиной понимают все то, что может быть измерено и выражено числом (числами).
Переменной величиной называют величину, которая принимает различные численные значения; величина, которая сохраняет одно и тоже численное значение, называется постоянной.

Переменная величина считается заданной, если задана совокупность её значений. Совокупность значений переменной величины называется областью изменения переменной величины.

Переменная величина называется непрерывной, если областью её изменения является некоторый интервал. Переменная величина называется дискретной, если областью её изменения является множество изолированных точек.

Переменная величина называется упорядоченной, если из двух значений переменной величины можно указать предыдущую и последующую.
Если переменная величина в области изменения убывает или возрастает, то она называется монотонной.
Если значения переменной величины таковы, что число будет больше (меньше) любого значения переменной величины, то говорят, что переменная величина ограниченна сверху (снизу). Переменная величина называется ограниченной, если она ограничена сверху и снизу.

Раздел IV
Введение в математический анализ
Глава 1
Функция
к.п.н. Безотечество Мила Михайловна, кафедра ФЕО ИЦМиМ СФУ
Параграф 2
Функции одной и нескольких переменных

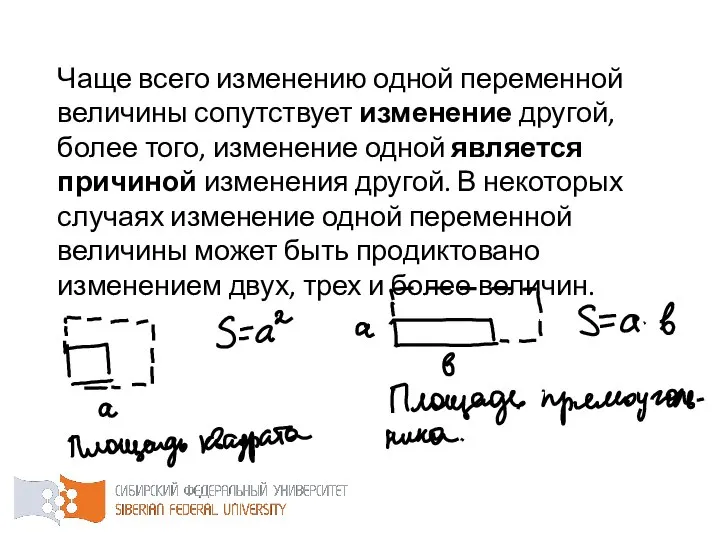
Чаще всего изменению одной переменной величины сопутствует изменение другой, более того, изменение одной является причиной изменения другой. В некоторых случаях изменение одной переменной величины может быть продиктовано изменением двух, трех и более величин.

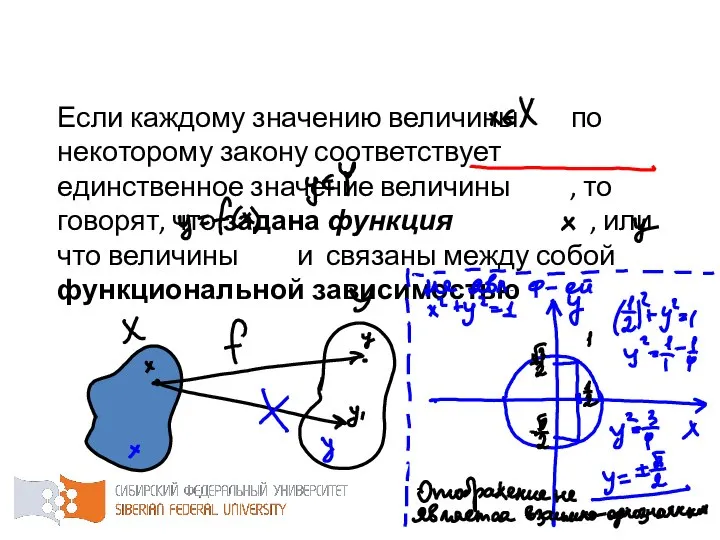
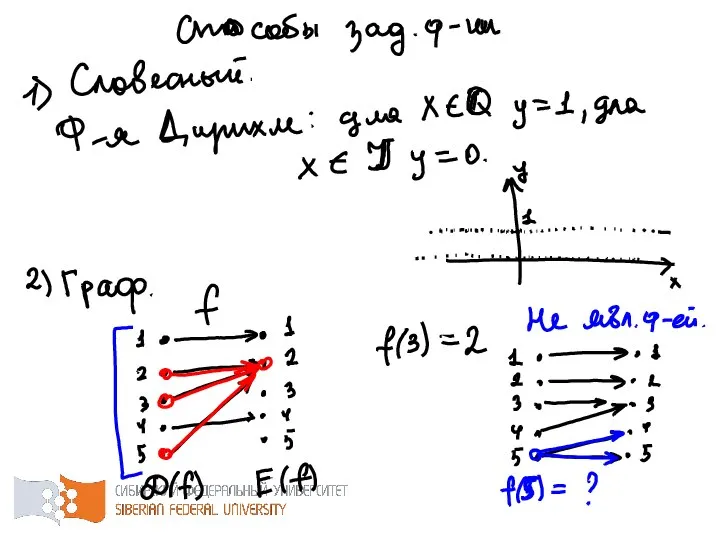
Если каждому значению величины по некоторому закону соответствует единственное значение величины , то говорят, что задана функция , или что величины и связаны между собой функциональной зависимостью

При этом, – аргумент функции (независимая переменная),
– значение функции (зависимая переменная), – закон соответствия,
– функция одной независимой переменной.

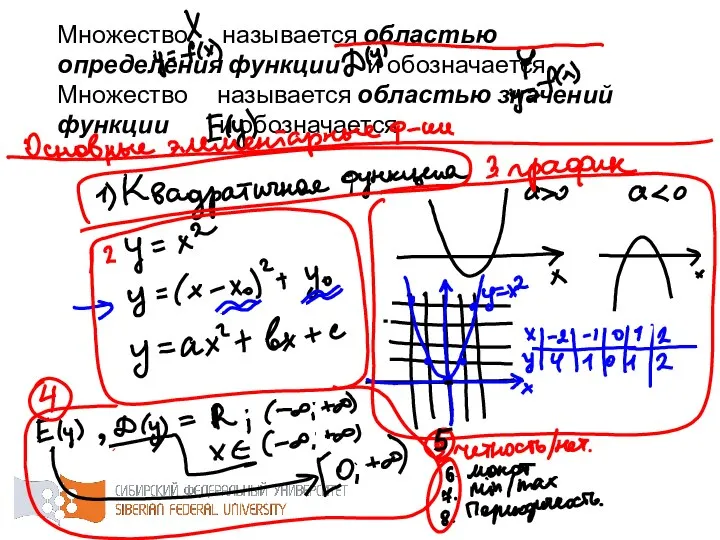
Множество называется областью определения функции и обозначается . Множество называется областью значений функции и обозначается .

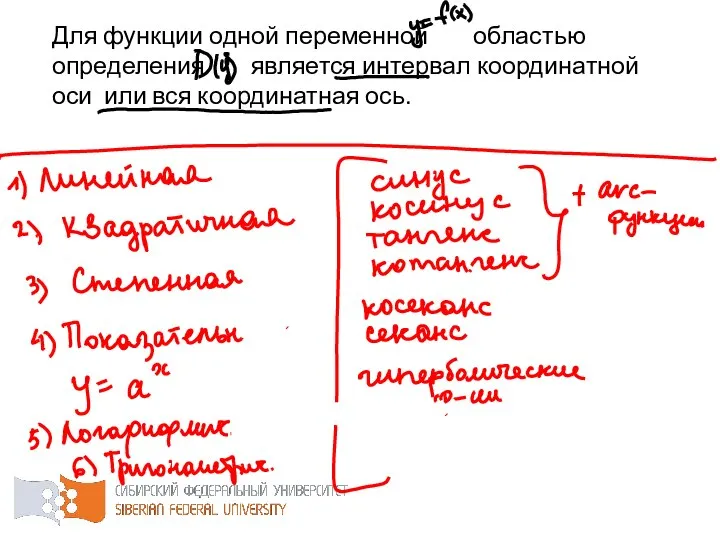
Для функции одной переменной областью определения является интервал координатной оси или вся координатная ось.

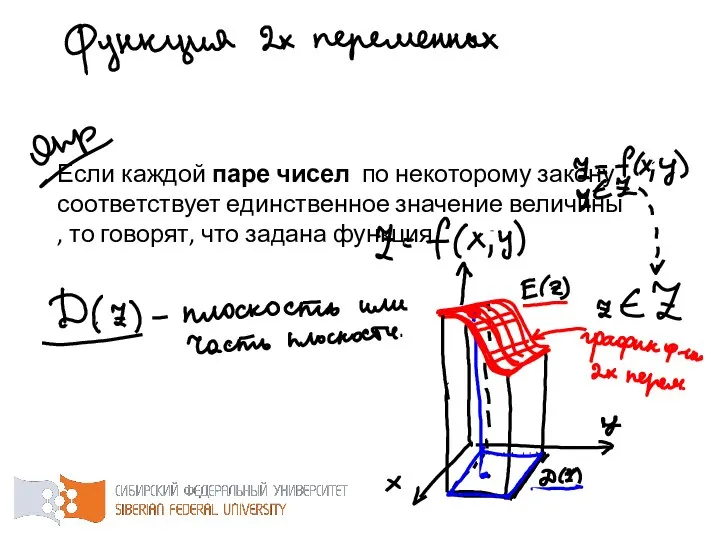
Если каждой паре чисел по некоторому закону соответствует единственное значение величины , то говорят, что задана функция

При этом – аргументы функции (независимые переменные), – значение функции (зависимая переменная), – закон соответствия, – функция двух независимых переменных, – область определения функции,
– область значений функции.

Для функции двух переменных область определения является часть координатной плоскости или вся координатная плоскость.

СВОЙСТВА ФУНКЦИИ
Непрерывность
Четность
Периодичность
Нули функции
Промежутки знакопостоянства
Монотонность
Экстремумы функции
Точки перегиба. Выпуклость

0 х1 < х2 х
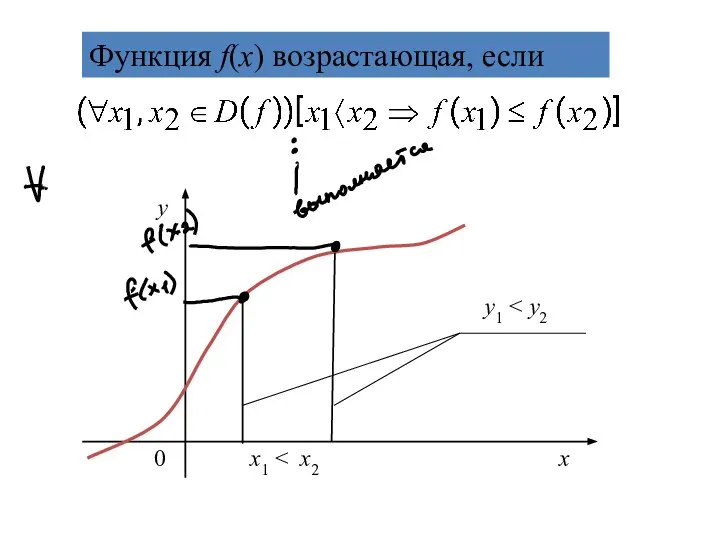
Функция f(х) возрастающая, если

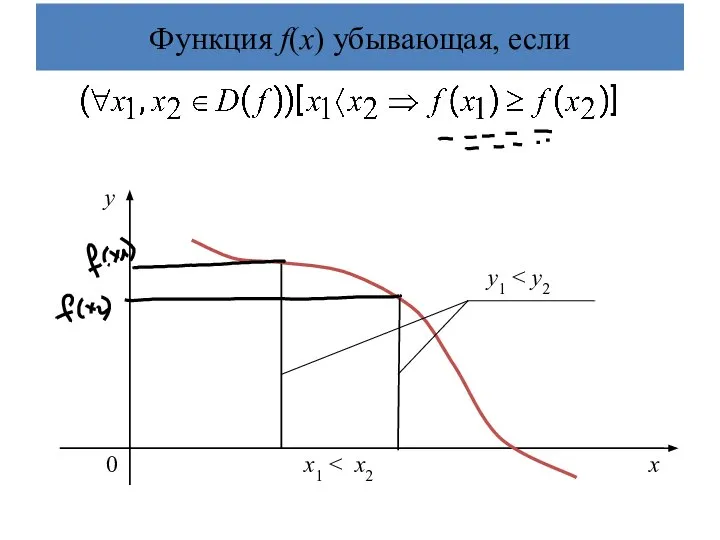
Функция f(х) убывающая, если
0 х1 < х2 х

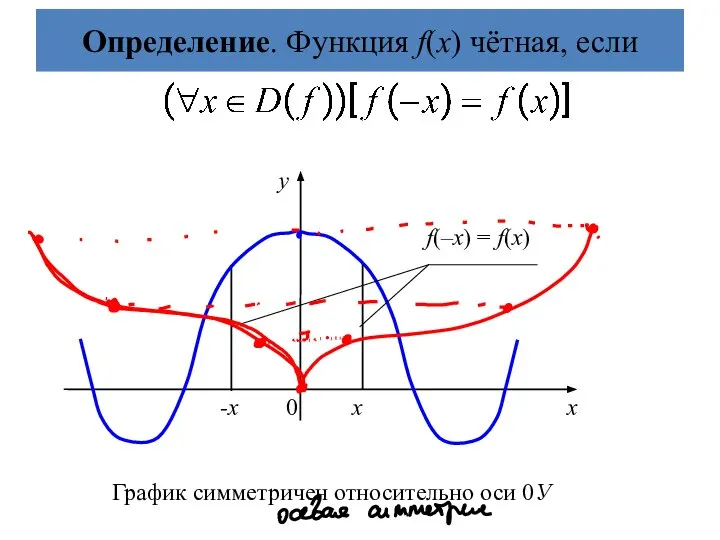
Определение. Функция f(х) чётная, если
f(–х) = f(х)
-х 0 х х
у
График симметричен относительно оси 0У

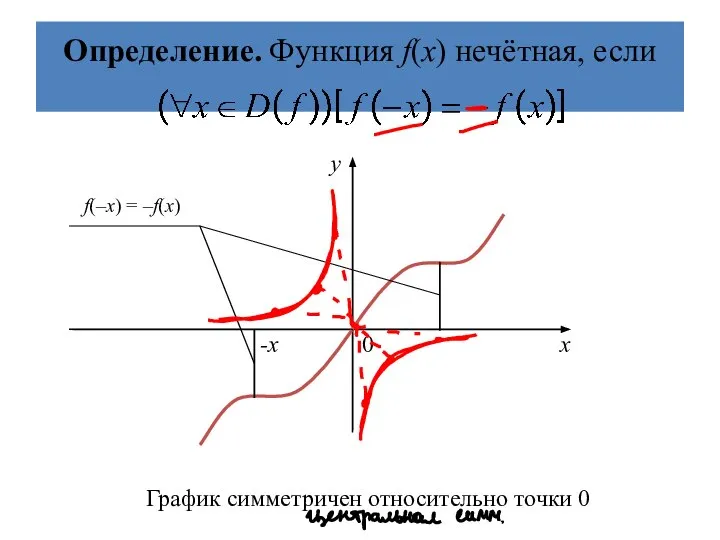
Определение. Функция f(х) нечётная, если
График симметричен относительно точки 0

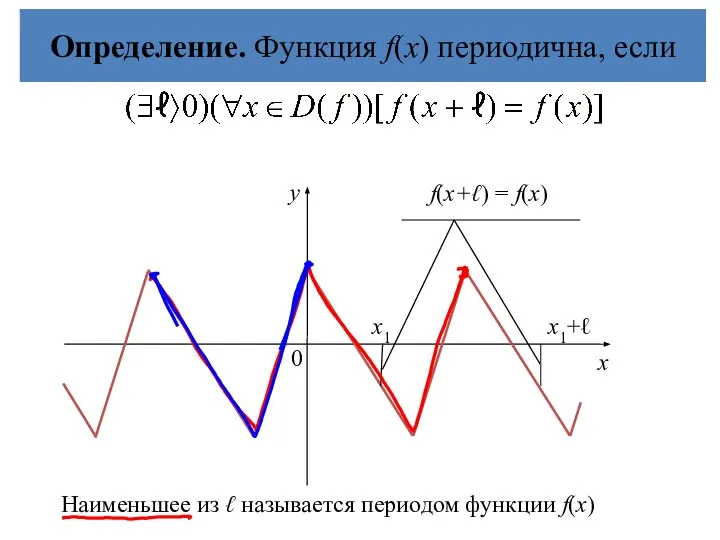
Определение. Функция f(х) периодична, если
f(х+ℓ) = f(х)
у
0
х
Наименьшее из ℓ называется периодом функции f(х)
х1
х1+ℓ

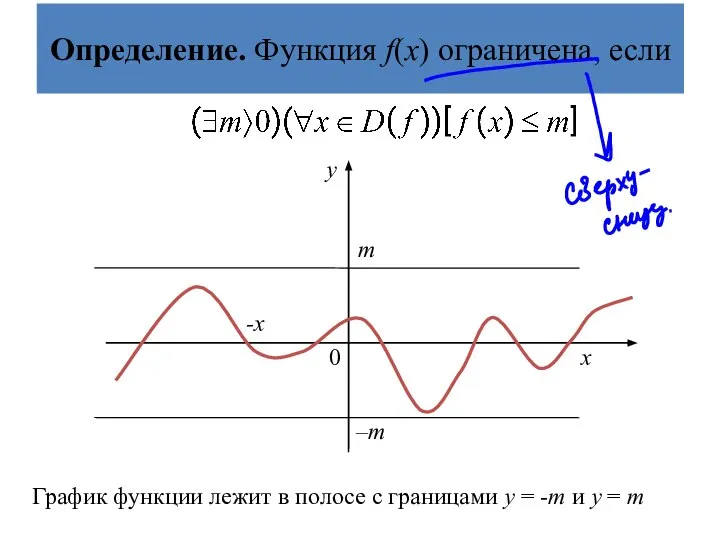
Определение. Функция f(х) ограничена, если
График функции лежит в полосе с границами у = -m и у = m

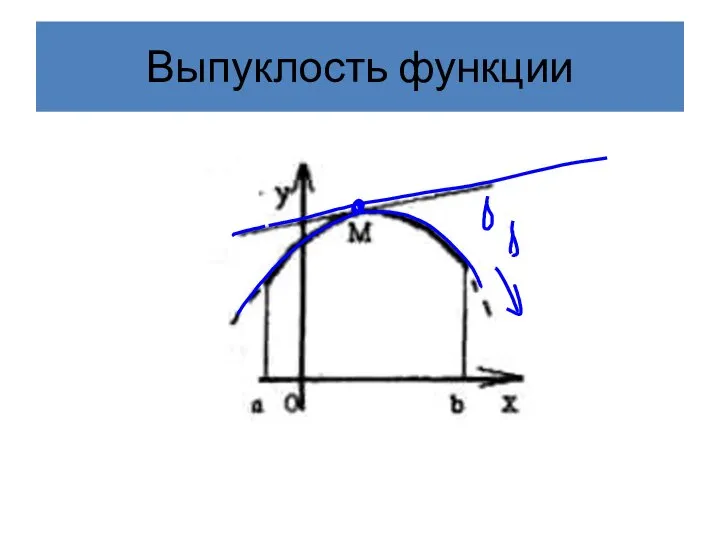
Выпуклость функции

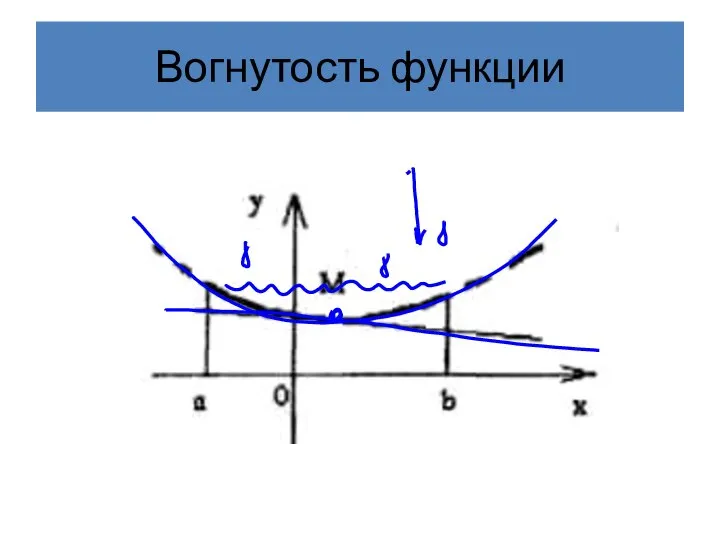
Вогнутость функции

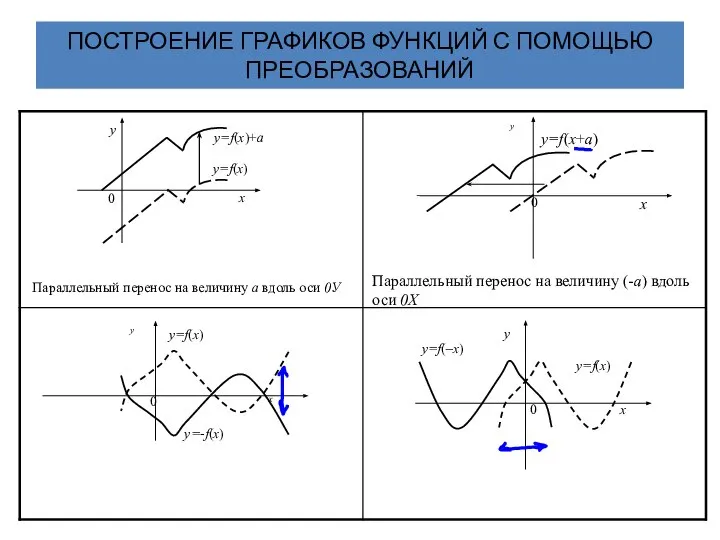
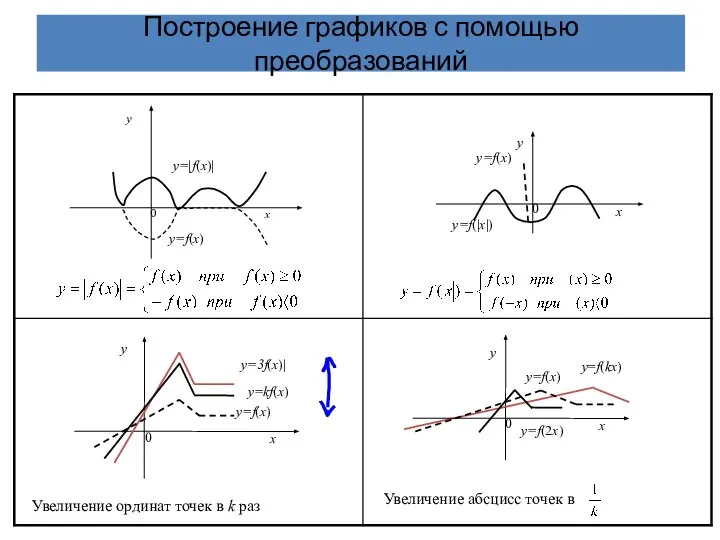
ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЙ
Параллельный перенос на величину а вдоль оси 0У
Параллельный перенос на величину (-а) вдоль оси 0Х

Построение графиков с помощью преобразований
Увеличение ординат точек в k раз
Увеличение абсцисс точек в
у=kf(х)
у=f(kх)

Раздел IV
Введение в математический анализ
Глава 2
Пределы
к.п.н. Безотечество Мила Михайловна, кафедра ФЕО ИЦМиМ СФУ
Параграф 1
Предел переменной величины

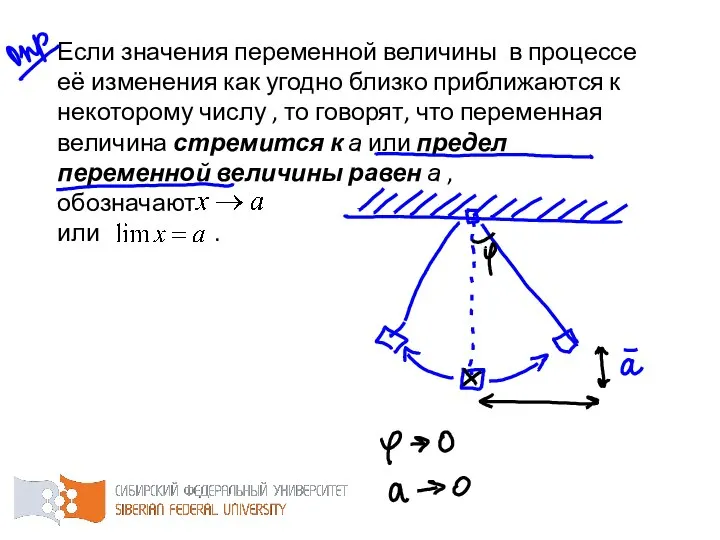
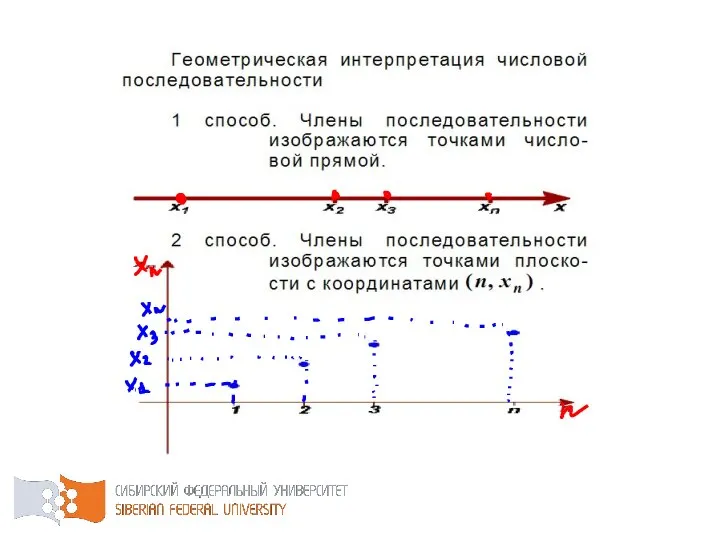
Если значения переменной величины в процессе её изменения как угодно близко приближаются к некоторому числу , то говорят, что переменная величина стремится к а или предел переменной величины равен а ,
обозначают
или .

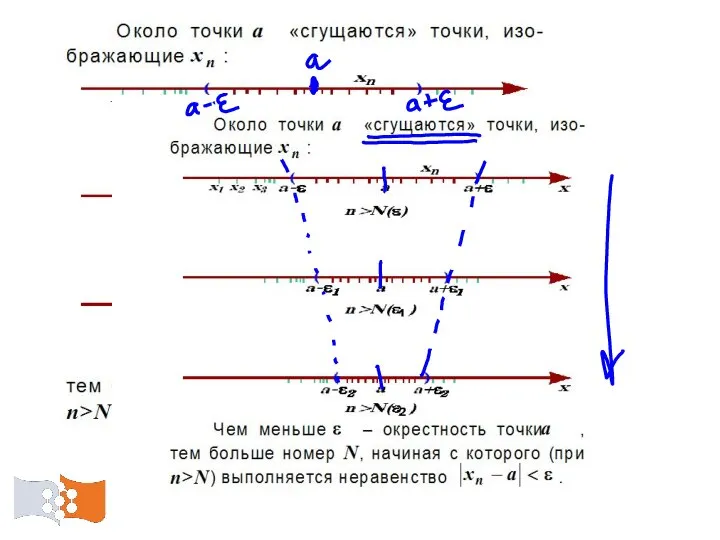
Пусть – некоторое значение переменной величины и – сколь угодно малое положительное число. Все точки интервала (кроме самой точки ),
удовлетворяющие неравенству , образуют – окрестность точки.

Иначе говоря, если – предел переменной величины , то все значения переменной величины , большие , попадут в – окрестность точки .
Предел переменной величины

Раздел IV
Введение в математический анализ
Глава 2
Пределы
к.п.н. Безотечество Мила Михайловна, кафедра ФЕО ИЦМиМ СФУ
Параграф 2
Предел последовательности

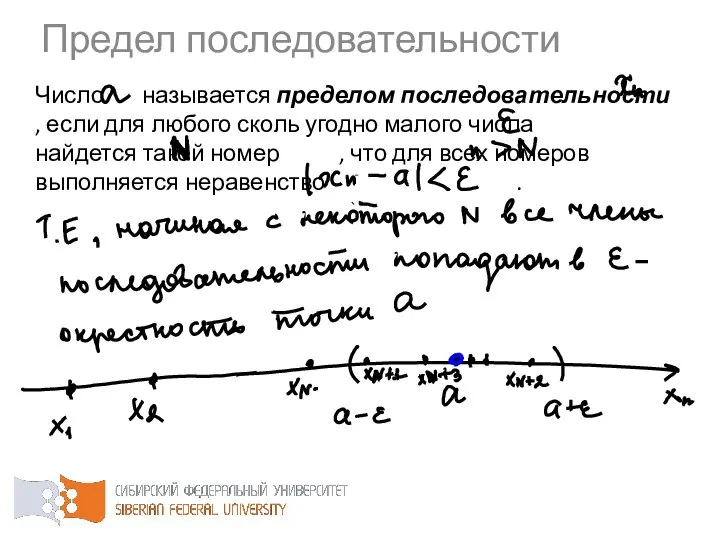
Число называется пределом последовательности , если для любого сколь угодно малого числа найдется такой номер , что для всех номеров выполняется неравенство .
Предел последовательности

Раздел IV
Введение в математический анализ
Глава 2
Пределы
к.п.н. Безотечество Мила Михайловна, кафедра ФЕО ИЦМиМ СФУ
Параграф 3
Предел функции одной переменной

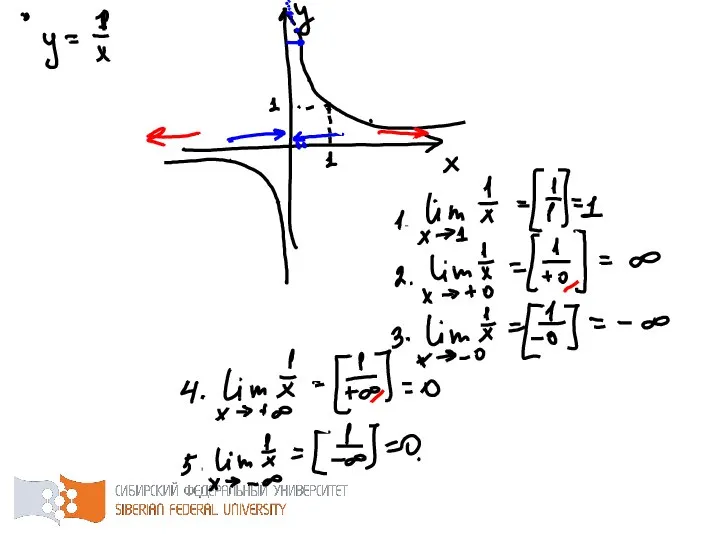
Число называется пределом функции в точке (или при ), если для любого наперед заданного сколь угодно малого , найдется такое число , что для всех , удовлетворяющих условию , выполняется неравенство .
Предел функции одной переменной
Иначе говоря, если , то точки графика функции с абсциссами из – окрестности точки и соответствующими им ординатами из ‑ окрестности точки должны лежать в полосе, ограниченной двумя прямыми и

Предел функции в бесконечной точке

Раздел IV
Введение в математический анализ
Глава 2
Пределы
к.п.н. Безотечество Мила Михайловна, кафедра ФЕО ИЦМиМ СФУ
Параграф 4
Односторонние пределы

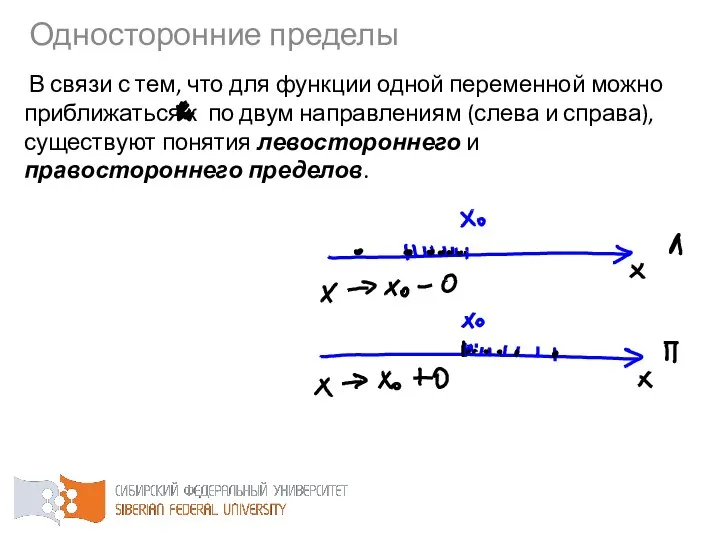
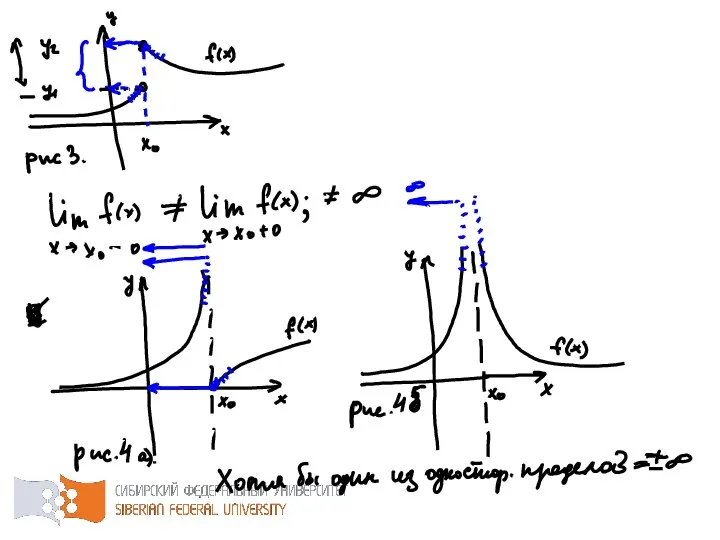
В связи с тем, что для функции одной переменной можно приближаться к по двум направлениям (слева и справа), существуют понятия левостороннего и правостороннего пределов.
Односторонние пределы

Число называется левосторонним пределом функции в точке , если для любого сколь угодно малого наперед заданного числа , найдется такое число , что при выполняется неравенство .
Иначе говоря, если слева (оставаясь меньше ), то предел функции – левосторонний, записывается в виде .
Число называется правосторонним пределом функции в точке , если для любого сколь угодно малого наперед заданного числа , найдется такое число , что при выполняется неравенство .
Иначе говоря, если справа (оставаясь больше ), то предел функции – правосторонний, записывается в виде .
Односторонние пределы

Односторонние пределы

Раздел IV
Введение в математический анализ
Глава 2
Пределы
к.п.н. Безотечество Мила Михайловна, кафедра ФЕО ИЦМиМ СФУ
Параграф 6
Бесконечно большие величины
Бесконечно малые величины

Раздел IV
Введение в математический анализ
Глава 2
Пределы
к.п.н. Безотечество Мила Михайловна, кафедра ФЕО ИЦМиМ СФУ
Параграф 7
Замечательные пределы

Раздел IV
Введение в математический анализ
Глава 2
Пределы
к.п.н. Безотечество Мила Михайловна, кафедра ФЕО ИЦМиМ СФУ
Параграф 8
Точки разрыва функции и их классификация

Функция в точке может быть
непрерывна,
терпеть устранимый разрыв (разрыв I рода), разрыв «скачек» (разрыв I рода),
бесконечный разрыв (разрыв II рода).

Раздел IV
Введение в математический анализ
Глава 2
Пределы
к.п.н. Безотечество Мила Михайловна, кафедра ФЕО ИЦМиМ СФУ
Параграф 9
Приращение функции

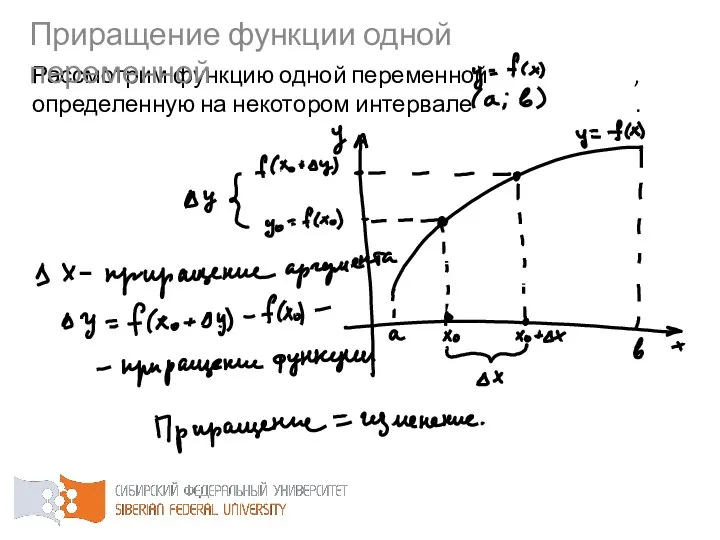
Рассмотрим функцию одной переменной , определенную на некотором интервале .
Приращение функции одной переменной

Рассмотрим функцию двух переменных , определенную на в некоторой области .
Приращение функции двух переменных

Раздел IV
Введение в математический анализ
Глава 3
Производная и дифференциал
к.п.н. Безотечество Мила Михайловна, кафедра ФЕО ИЦМиМ СФУ
Параграф 1
Основные определения

Раздел IV
Введение в математический анализ
Глава 3
Производная и дифференциал
к.п.н. Безотечество Мила Михайловна, кафедра ФЕО ИЦМиМ СФУ
Параграф 2
Правила вычисления производных

Раздел IV
Введение в математический анализ
Глава 3
Производная и дифференциал
к.п.н. Безотечество Мила Михайловна, кафедра ФЕО ИЦМиМ СФУ
Параграф 3
Физический (механический) смысл производных

Раздел IV
Введение в математический анализ
Глава 3
Производная и дифференциал
к.п.н. Безотечество Мила Михайловна, кафедра ФЕО ИЦМиМ СФУ
Параграф 4
Геометрический смысл производных

Раздел IV
Введение в математический анализ
Глава 3
Производная и дифференциал
к.п.н. Безотечество Мила Михайловна, кафедра ФЕО ИЦМиМ СФУ
Параграф 4
Производная неявно заданной функции