Слайд 2Здравствуйте, внимательно изучите тему, рассмотрите пример нахождения интеграла
Слайд 4Вопросы для повторения
1. Что называют криволинейной трапецией?
2. Являются ли фигуры, изображённые на
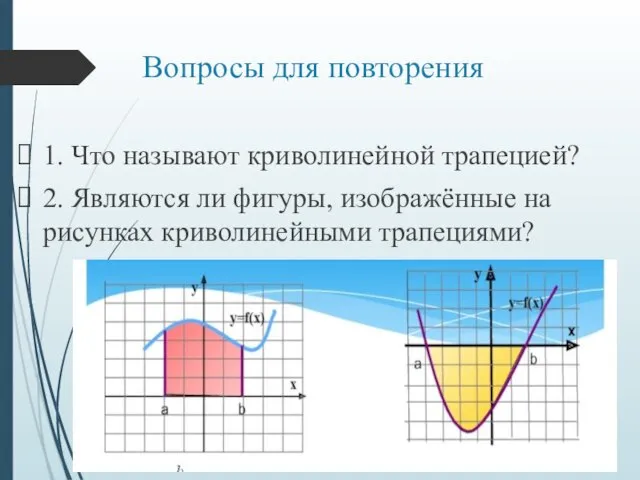
рисунках криволинейными трапециями?
Слайд 53. Запишите формулу для вычисления площади криволинейной трапеции

Слайд 6Рассмотрим другой подход к вычислению площади криволинейной трапеции
Будем считать функцию f неотрицательной

и непрерывной на отрезке [а; в], тогда площадь S соответствующей криволинейной трапеции можно приближённо подсчитать следующим образом
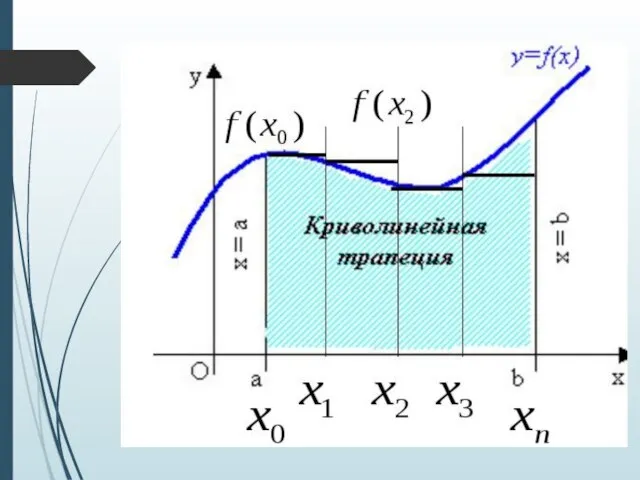
Слайд 8Разобьём отрезок [а; в] на n отрезков одинаковой длины точками
![Разобьём отрезок [а; в] на n отрезков одинаковой длины точками](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/895487/slide-7.jpg)
Слайд 9 При n → ∞
Sn→ к некоторому числу
Это число называют интегралом

функции f от а до в и обозначают:
в
∫ f(х)dх
а
Слайд 10
Числа а и в - называются пределами
интегрирования, а

– нижним пределом, в – верхним.
Знак ∫ - называют знаком интеграла
Функцию f называют подынтегральной функцией, а переменная х – переменной интегрирования
df- знак дифференциала
Слайд 11 Итак, если f( х ) ≥0 на отрезке [а; в], то
![Итак, если f( х ) ≥0 на отрезке [а; в], то площадь](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/895487/slide-10.jpg)
площадь соответствующей криволинейной трапеции выражается формулой:
в
S = ∫ f(х)dх
а
Слайд 12Сравнивая формулы криволинейных трапеций :
в
S = ∫ f(х)dх и S

= F(в) – F(а)
а
Делаем вывод:
Слайд 14Иссак Ньютон
(1643-1716)
Готфрид
Лейбниц(1646-1716).






![Разобьём отрезок [а; в] на n отрезков одинаковой длины точками](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/895487/slide-7.jpg)


![Итак, если f( х ) ≥0 на отрезке [а; в], то площадь](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/895487/slide-10.jpg)




 Случаи вычитания 15-
Случаи вычитания 15- Первообразная и интеграл
Первообразная и интеграл Эконометрика как наука
Эконометрика как наука Презентация на тему Натуральные числа 5 класс
Презентация на тему Натуральные числа 5 класс  Умножение на 0. 3 класс
Умножение на 0. 3 класс Число и цифра 5. (с.34 - 35)
Число и цифра 5. (с.34 - 35) Διδακτική Ενότητα Α: Συνδυαστική Ανάλυση
Διδακτική Ενότητα Α: Συνδυαστική Ανάλυση Бесконечные периодические десятичные дроби
Бесконечные периодические десятичные дроби Подобные треугольники. 8 класс
Подобные треугольники. 8 класс Соотношения между сторонами и углами прямоугольного треугольника. Задачи на готовых чертежах
Соотношения между сторонами и углами прямоугольного треугольника. Задачи на готовых чертежах Дидактические игры на уроках математики
Дидактические игры на уроках математики Неравенства. Проверь примеры
Неравенства. Проверь примеры Умножение десятичных дробей. Графический диктант
Умножение десятичных дробей. Графический диктант Логическая закономерность, лежащая в основе подбора алгебраических дробей
Логическая закономерность, лежащая в основе подбора алгебраических дробей Письмо цифры 6
Письмо цифры 6 Инварианты. Общее уравнение кривой второго порядка
Инварианты. Общее уравнение кривой второго порядка Математическая игра
Математическая игра Занимательная математика
Занимательная математика Математические игры и задачи
Математические игры и задачи Презентация на тему Уравнения в ЕГЭ по математике: примеры и решения
Презентация на тему Уравнения в ЕГЭ по математике: примеры и решения  Пропорциональные отрезки в прямоугольном треугольнике
Пропорциональные отрезки в прямоугольном треугольнике Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Приёмы устных вычислений вида: 470 + 80, 560 - 90
Приёмы устных вычислений вида: 470 + 80, 560 - 90 Ментальный счет
Ментальный счет Методы оптимальных решений
Методы оптимальных решений Правильные многоугольники
Правильные многоугольники Учебно-исследовательская работа Счастливый случай или точный расчёт
Учебно-исследовательская работа Счастливый случай или точный расчёт Презентация на тему РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ
Презентация на тему РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ