Интегрирование рациональных функций

Дробно – рациональная функция
Дробно – рациональной функцией называется функция, равная отношению двух многочленов:
Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя, то есть m < n , в противном случае дробь называется неправильной.
Всякую неправильную рациональную дробь можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби:

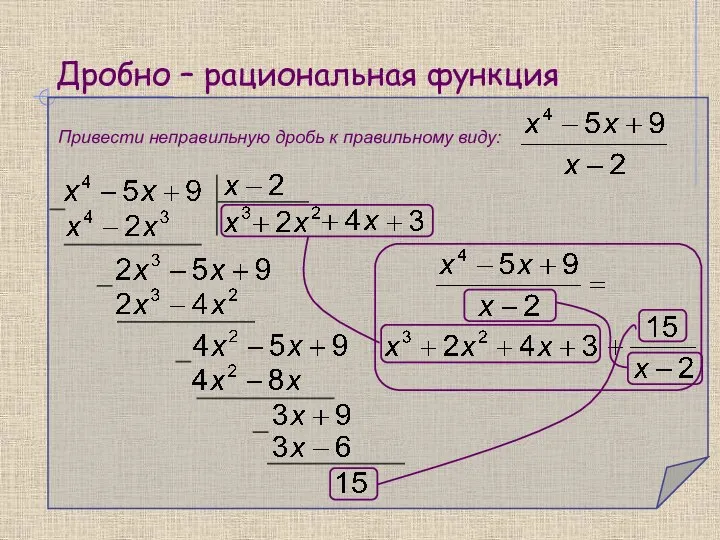
Дробно – рациональная функция
Привести неправильную дробь к правильному виду:

Простейшие рациональные дроби
Правильные рациональные дроби вида:
Называются простейшими рациональными дробями
типов.

Разложение рациональной дроби на простейшие дроби
Теорема: Всякую правильную рациональную дробь , знаменатель которой разложен на множители:
можно представить, притом единственным образом в виде суммы простейших дробей:

Разложение рациональной дроби на простейшие дроби
Поясним формулировку теоремы на следующих примерах:
Для нахождения неопределенных коэффициентов A, B, C, D… применяют два метода: метод сравнивания коэффициентов и метод частных значений переменной. Первый метод рассмотрим на примере.

Разложение рациональной дроби на простейшие дроби
Представить дробь в виде суммы простейших дробей:

Интегрирование простейших дробей
Найдем интегралы от простейших рациональных дробей:
Интегрирование дроби 3 типа рассмотрим на примере.

Интегрирование простейших дробей

Интегрирование простейших дробей
Интеграл данного типа с помощью подстановки:
приводится к сумме двух интегралов:
Первый интеграл вычисляется методом внесения t под знак дифференциала.
Второй интеграл вычисляется с помощью рекуррентной формулы:

Интегрирование простейших дробей
a = 1; k = 3

Общее правило интегрирования рациональных дробей
Если дробь неправильная, то представить ее в виде суммы многочлена и правильной дроби.
Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших дробей с неопределенными коэффициентами
Найти неопределенные коэффициенты методом сравнения коэффициентов или методом частных значений переменной.
Проинтегрировать многочлен и полученную сумму простейших дробей.

Пример
Приведем дробь к правильному виду.

Пример