Содержание
- 2. Иррациональные неравенства Сегодня на занятии мы рассмотрим способы решений двух видов неравенств, которые могут пригодиться при
- 3. Первое, что мы должны заметить, корень квадратный извлекается только из положительных чисел, так что f(x)≥0. Второе,
- 4. Иррациональные неравенства И так при решении иррациональных неравенств можно переходить к следующей системе неравенств:
- 5. Иррациональные неравенства Теперь давайте рассмотрим неравенство вида f(x)≥0 – это безусловное условие которое должно накладываться как
- 6. Иррациональные неравенства. И так, неравенство равносильно следующей совокупности систем:
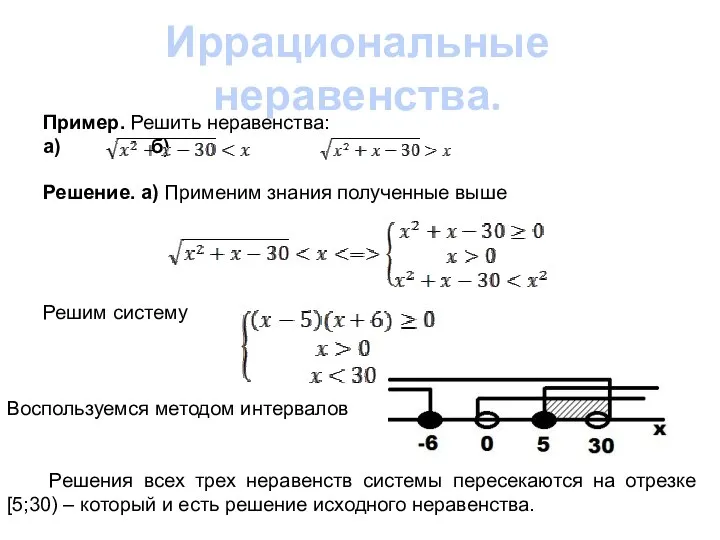
- 7. Иррациональные неравенства. Пример. Решить неравенства: а) б) Решение. а) Применим знания полученные выше Решим систему Воспользуемся
- 8. Иррациональные неравенства. б) Нам нужно решить совокупность двух систем: Решения каждой системы очевидны, даже не применяя
- 9. Неравенства с модулями. Неравенства, которые содержат переменную под знаком модуля, могут решаться разными методами. Мы рассмотрим
- 10. Неравенства с модулями. Второй способ. Обе части нашего неравенства неотрицательны, тогда воспользовавшись теоремой 5 равносильности неравенств,
- 11. Неравенства с модулями. Третий способ. В зависимости от знака выражения 3х-6, мы можем раскрыть модуль двумя
- 12. Неравенства с модулями. Пример. Решить неравенство: Решение. Модуль может раскрываться двумя способами: 1. Если 2. Если
- 13. Неравенства с модулями. Для каждой системы построим интервалы решения. хϵ(-∞;-4)U[3;+∞) хϵ(-4;3] Осталось объединить два промежутка и
- 14. Иррациональные неравенства. Неравенства с модулями. Задачи для самостоятельного решения. 1. Решить неравенства: а) б) 2. Решить
- 16. Скачать презентацию










![Неравенства с модулями. Для каждой системы построим интервалы решения. хϵ(-∞;-4)U[3;+∞) хϵ(-4;3] Осталось](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1092221/slide-12.jpg)

 Решение задач на проценты. Концентрация
Решение задач на проценты. Концентрация Дифференциальные уравнения (продолжение)
Дифференциальные уравнения (продолжение) Дифференциальные уравнения. Лекция 3
Дифференциальные уравнения. Лекция 3 Первый признак равенства треугольников. Теорема
Первый признак равенства треугольников. Теорема Сложение дробей
Сложение дробей Функции и литература
Функции и литература Решение задач на работу
Решение задач на работу Линейка. Построение прямых линий и отрезков. Измерение сторон геометрических фигур
Линейка. Построение прямых линий и отрезков. Измерение сторон геометрических фигур Основи векторної графіки
Основи векторної графіки Неравенства. Тест
Неравенства. Тест Нахождение общего количества единиц определённого разряда в данном числе
Нахождение общего количества единиц определённого разряда в данном числе Презентация на тему Графическое решение квадратных уравнений (8 класс)
Презентация на тему Графическое решение квадратных уравнений (8 класс)  Влияние математических действий на аликвоты. возникновения аликвот
Влияние математических действий на аликвоты. возникновения аликвот Правила вычисления производных
Правила вычисления производных Центральные и вписанные углы
Центральные и вписанные углы Занимательная математика
Занимательная математика Регрессионный анализ
Регрессионный анализ Сравнение групп предметов
Сравнение групп предметов Сводка и группировка статистических данных
Сводка и группировка статистических данных Использование краеведческого материала на уроках математики
Использование краеведческого материала на уроках математики Способы решения квадратных уравнений
Способы решения квадратных уравнений Математическая логика. Упорядоченные множества. Прямое произведение множеств. Бинарные отношения
Математическая логика. Упорядоченные множества. Прямое произведение множеств. Бинарные отношения Перпендикулярные прямые
Перпендикулярные прямые Перевод величин
Перевод величин Построение сечений в многогранниках
Построение сечений в многогранниках История метрологии и теории измерений
История метрологии и теории измерений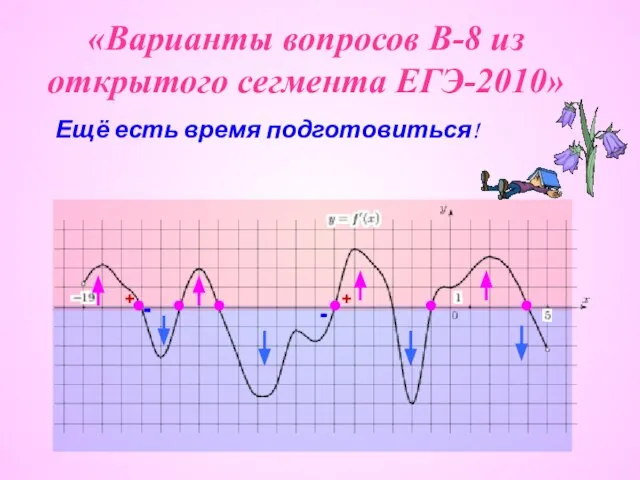 Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010
Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010 Черчение геометрических фигур не отрывая карандаш от бумаги
Черчение геометрических фигур не отрывая карандаш от бумаги