Содержание
- 2. Анализ - логический прием, метод исследования, состоящий в том, что изучаемый объект мысленно (или практически) расчленяется
- 3. В математике, чаще всего, под анализом понимают рассуждение в «обратном направлении», то есть от неизвестного, от
- 4. Синтез, опираясь на данные, полученные в ходе анализа, дает решение задачи или доказательство теоремы. Анализ лежит
- 5. Из такого понимания элементарной задачи следует, что чем больший опыт решения задач, тем больше задач становятся
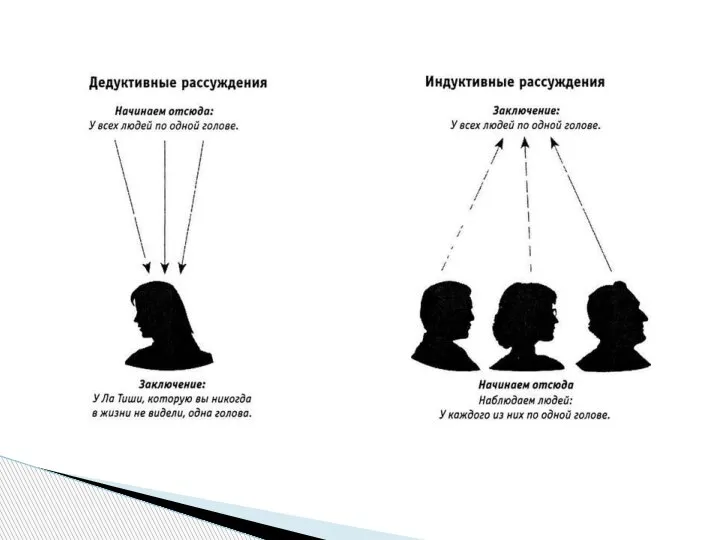
- 6. Дедукция (от лат. выведение)- умозаключение от общего к частному, частичному или от более общего к менее
- 7. Как в любых процессах познания (научного или обыденного), так и в процессе обучения дедукция и индукция
- 8. В процессе обучения индуктивный и дедуктивный методы используются в единстве Индуктивный метод используется тогда, когда изучается
- 10. Джоэль сильнее Билла, но слабее Ричарда. Ричард сильнее Джоэля, но слабее Дональда. Кто из них самый
- 11. индуктивно-дедуктивному способу, когда объяснение начинается с индукции и переходит затем в дедукцию (возможно, при значительном перевесе
- 14. Скачать презентацию










 Алгоритмы на графах
Алгоритмы на графах Устная нумерация чисел от 1 до 20
Устная нумерация чисел от 1 до 20 Числовi послiдовностi. Властивостi числових послiдовностей
Числовi послiдовностi. Властивостi числових послiдовностей Решение тригонометрических уравнений
Решение тригонометрических уравнений Окружность
Окружность Предел последовательности
Предел последовательности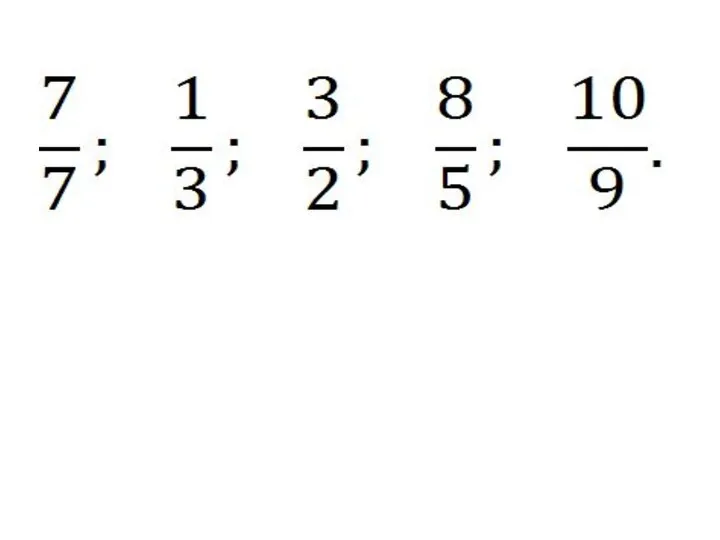 Знак деления
Знак деления Деление одночлена на одночлен
Деление одночлена на одночлен Решаем задачи
Решаем задачи Системы принятия решений
Системы принятия решений Возвратные уравнения
Возвратные уравнения Математика: психология и нейронауки. Чем нейробиология и когнитивная психология могут помочь учителю математики?
Математика: психология и нейронауки. Чем нейробиология и когнитивная психология могут помочь учителю математики? Куб. Теорема Эйлера
Куб. Теорема Эйлера Решение иррациональных уравнений. Разные методы
Решение иррациональных уравнений. Разные методы Решение тригонометрических неравенств
Решение тригонометрических неравенств Тригонометрические уравнения и математические термины на английском языке
Тригонометрические уравнения и математические термины на английском языке Сложение и вычитание многочленов
Сложение и вычитание многочленов Производная функции. Тест 1
Производная функции. Тест 1 Основы дисперсионного анализа
Основы дисперсионного анализа Неопределённый интеграл. Элементы интегрального исчисления
Неопределённый интеграл. Элементы интегрального исчисления Сравнение предметов. Счет до 5
Сравнение предметов. Счет до 5 Формулы половинного аргумента
Формулы половинного аргумента Пирамида и её элементы. Правильная пирамида
Пирамида и её элементы. Правильная пирамида Шар. Куб. Параллелепипед
Шар. Куб. Параллелепипед Преподаватель математики и информатики ГБОУ СПО РО «Константиновский педагогический колледж» Алексей Юлия Вадимовна
Преподаватель математики и информатики ГБОУ СПО РО «Константиновский педагогический колледж» Алексей Юлия Вадимовна Таблицы истинности
Таблицы истинности Плоскость касательной к сфере
Плоскость касательной к сфере Задачи на готовых чертежах. Ромб
Задачи на готовых чертежах. Ромб