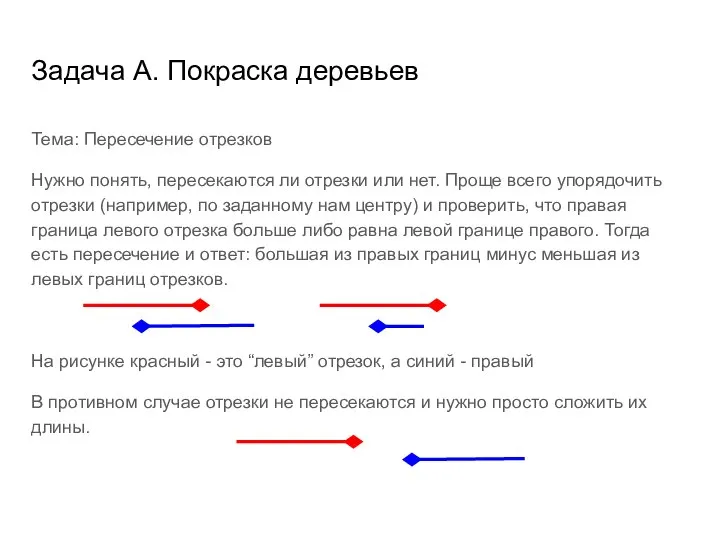
Слайд 10Задача I: Строки Фибоначчи
Темы: Динамическое программирование, рекуррентные соотношения
Для каждой позиции в строке

легко определить, есть ли начаиная с неё F(1, X, Y), F(2, X, Y) и F(3, X, Y), удобно также отдельно посчитать F(4, X, Y).
Обозначим за G(pos, i, X, Y) функцию, возвращающую истину, если начиная с позиции pos идет F(i, X, Y). Тогда G(pos, i + 1, X, Y) = G(pos, i, X, Y) and G(pos + fib(i), i - 1, X, Y), где fib(i) - i-ое число Фибоначчи (совпадающее с длиной i-ой строки Фибоначчи). Достаточно посчитать эти функции в порядке возрастания i. Можно делать это эффективно, не перебирая X, Y, а определяя их по первым буквам.
Сложность такого решения O(NlogN), т.к. числа Фибоначчи растут примерно как 2N
Также возможно решение с использованием хешей.









 Конструктор (3)
Конструктор (3) Площадь сферы
Площадь сферы Единицы измерения площадей
Единицы измерения площадей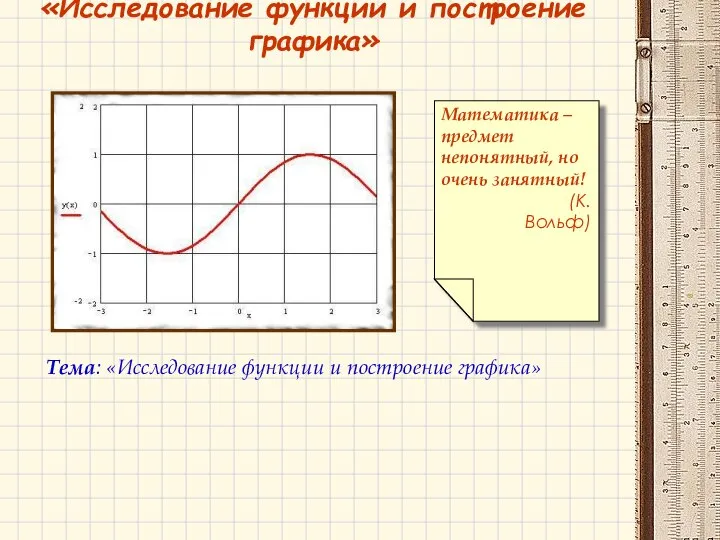 Функция и построение графика
Функция и построение графика Математика в биологии
Математика в биологии Вычисления. 5 класс
Вычисления. 5 класс Решение тригонометрических уравнений
Решение тригонометрических уравнений Подготовка к ВПР (8 класс)
Подготовка к ВПР (8 класс) Устойчивость движения. Фазовая плоскость. Классификация точек покоя
Устойчивость движения. Фазовая плоскость. Классификация точек покоя Матрицы и системы линейных уравнений
Матрицы и системы линейных уравнений Свойства умножения
Свойства умножения Устный счет ( 3 класс )
Устный счет ( 3 класс ) Сборник по подготовке к государственной итоговой аттестации по геометрии
Сборник по подготовке к государственной итоговой аттестации по геометрии Подобные треугольники. (8 класс)
Подобные треугольники. (8 класс) Векторы на плоскости
Векторы на плоскости Параллельные прямые. Задачи сказочных героев
Параллельные прямые. Задачи сказочных героев Теория и практика статистических выводов. Лекция 3
Теория и практика статистических выводов. Лекция 3 Решение простейших тригонометрических неравенств
Решение простейших тригонометрических неравенств Пробный урок
Пробный урок Понятие площади. Площадь квадрата и прямоугольника
Понятие площади. Площадь квадрата и прямоугольника Сокращение дробей. Самоанализ
Сокращение дробей. Самоанализ Презентация на тему Параллельные прямые
Презентация на тему Параллельные прямые  Возведение степени в степень
Возведение степени в степень Нахождение числа по его дроби
Нахождение числа по его дроби Преобразование иррациональных выражений
Преобразование иррациональных выражений Связность графов. Глава 2
Связность графов. Глава 2 Аналитическая запись функций алгебры логики
Аналитическая запись функций алгебры логики Презентация по математике "Решение задач с помощью систем уравнений второй степени" -
Презентация по математике "Решение задач с помощью систем уравнений второй степени" -