История аксиомы

Аксиомы в широком понятии
Аксиомами в различного рода системах знаний (теориях) называются базовые положения (правила, высказывания, утверждения),
служащие основами для дальнейших построений, и которые не могут быть доказаны, а также выведены из теории.

Кто создал аксиомы
ЛОБАЧЕВСКОГО ГЕОМЕТРИЯ
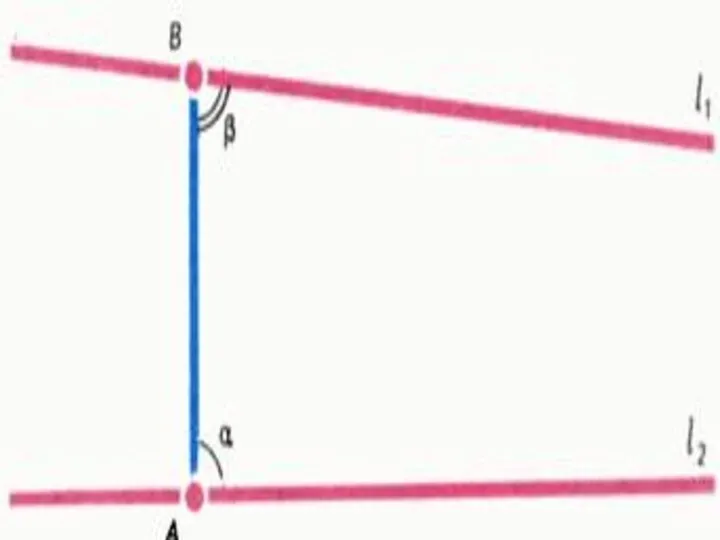
История создания геометрии Лобачевского одновременно является историей попыток доказать пятый постулат Евклида. Этот постулат представляет собой одну из аксиом, положенных Евклидом в основу изложения геометрии (см. Евклид и его «Начала»). Пятый постулат – последнее и самое сложное из предложений, включенных Евклидом в его аксиоматику геометрии. Напомним формулировку пятого постулата: если две прямые пересекаются третьей так, что по какую-либо сторону от нее сумма внутренних углов меньше двух прямых углов, то по эту же сторону исходные прямые пересекаются. Например, если на рис. 1 угол –

прямой, а угол чуть меньше прямого, то прямые и непременно пересекаются, причем справа от прямой . Многие теоремы Евклида (например, «вравнобедренном треугольнике углы при основании равны») выражают гораздо более простые факты, чем пятый постулат. К тому же проверить на эксперименте пятый постулат довольно сложно. Достаточно сказать, что если на рис. 1 расстояние считать равным 1 м, а угол отличается от прямого на одну угловую секунду, то можно подсчитать, что прямые и пересекаются на расстоянии свыше 200 км от прямой .

Николай Иванович Лобачевский

Николай Иванович Лобочевский