История развития математики в Древнем Египте и Индии

ЦЕЛЬ РЕФЕРАТА:
знакомство с историей математики в таких восточных странах, как Египет и Индия.

МАТЕМАТИЧЕСКИЕ ИСТОЧНИКИ ДРЕВНИХ ЕГИПТЯН

Назван так по имени своего первого владельца. Он был найден в 1858 г., расшифрован и издан в 1870 г. Рукопись представляла собой узкую (33 см) и длинную (5,25 м) полосу папируса, содержащую 84 задачи. Теперь одна часть папируса хранится в Британском музее в Лондоне, а другая находится в Нью-Йорке.
Папирус Райнда

Его в декабре 1888 г. Приобрел в Луксоре русский египтолог Владимир Семёнович Голенищев. Сейчас папирус принадлежит Государственному музею изобразительных искусств имени А. С. Пушкина. Этот свиток длиной 5,44 м и шириной 8 см включает 25 задач.
Московский папирус

С большим трудом распрямлен в 1927 г.
Во многом пролил свет на арифметические знания египтян. Ныне он хранится в Британском музее.
«Кожаный свиток египетской
математики»

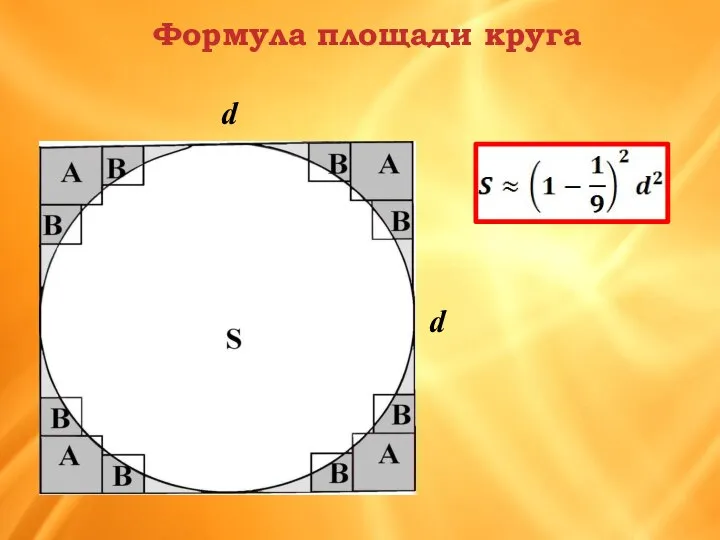
В папирусе Райнда приводится такое правило для вычисления площади произвольного четырехугольника: полусумму длин двух противоположных сторон четырехугольника умножить на полусумму длин двух других сторон.
В равенство оно превращается только для прямоугольника. Иначе говоря, египетское правило справедливо (и то не точно, а лишь приближенно), когда четырехугольник мало отличается от прямоугольника. По-видимому, именно такую форму имело большинство земельных участков египтян, и для них ошибка, заключенная в этом правиле, была незначительна.
О формуле площади четырехугольника
Но это правило неверно! Даже для параллелограмма оно не дает истинного значения площади. Вообще, для любого четырехугольника со сторонами a, b, c, d имеет место неравенство:
a
b
c
d

Формула площади круга
d
d

РАСКРЫТЫЕ ЗАГАДКИ ПИРАМИДЫ ХЕОПСА
Диагональ пирамиды дает абсолютно точное ее направление по меридиану, причем точность этого направления на теоретический северный полюс достигает 4 минуты 30 секунд.
Кроме того, этот меридиан, проходящий через Хеопсову пирамиду, делит на две равные части поверхность моря и суши, считая Америку и Тихий океан.
Широта, проходящая через центр пирамиды, делит также на две равные части весь земной шар, по количеству суши и воды.
При измерении самой пирамиды оказалось, что периметр пирамиды, разделенный на двойную высоту, дает точное число π, с точностью до одной стотысячной.

Священная мера длины Египта, т.е. пирамидальный дюйм (по странному совпадению равный современному английскому) есть одна миллиардная часть орбиты Земли, пройденной ею в 24 часа.
Другая линейная мера пирамиды – локоть, равная 25 дюймам, или 635,66 миллиметра – это одна десятимиллионная полярного радиуса Земли.
Сумма двух диагоналей пирамиды, выраженных в дюймах, дает число лет, в течение которых северный полюс нашей земли совершает один полный оборот.
Объем пирамиды, помноженный на удельный вес камня, из которого она сделана, дает теоретический вес земного шара.

ИНДИЙСКИЕ МАТЕМАТИКИ

Ариабхата

Брахмагупта

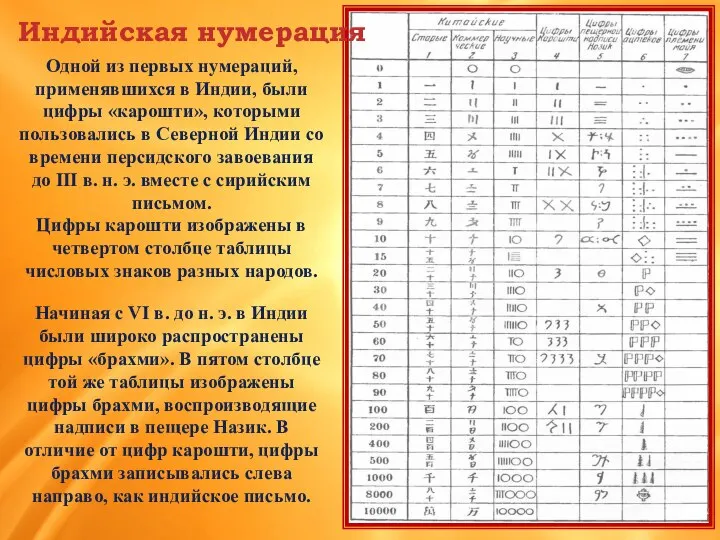
Индийская нумерация
Одной из первых нумераций, применявшихся в Индии, были цифры «карошти», которыми пользовались в Северной Индии со времени персидского завоевания до III в. н. э. вместе с сирийским письмом.
Цифры карошти изображены в четвертом столбце таблицы числовых знаков разных народов.
Начиная с VI в. до н. э. в Индии были широко распространены цифры «брахми». В пятом столбце той же таблицы изображены цифры брахми, воспроизводящие надписи в пещере Назик. В отличие от цифр карошти, цифры брахми записывались слева направо, как индийское письмо.

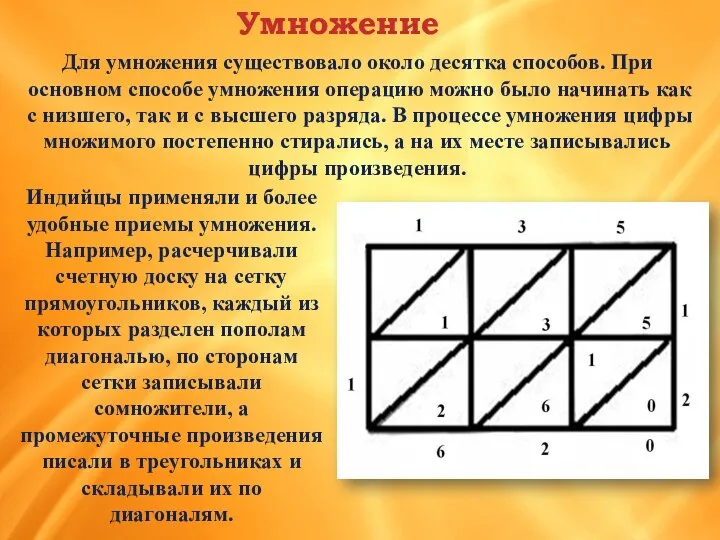
Индийцы применяли и более удобные приемы умножения. Например, расчерчивали счетную доску на сетку прямоугольников, каждый из которых разделен пополам диагональю, по сторонам сетки записывали сомножители, а промежуточные произведения писали в треугольниках и складывали их по диагоналям.
Для умножения существовало около десятка способов. При основном способе умножения операцию можно было начинать как с низшего, так и с высшего разряда. В процессе умножения цифры множимого постепенно стирались, а на их месте записывались цифры произведения.
Умножение

При работе над рефератом у меня сформировалось собственное мнение о том, что человечество не может развиваться без знания научного и культурного прошлого своих предков.
Заключение
В соответствии с целью реферата мною были изучены исторические сведения о математической науке Древнего Египта и Индии. Я узнала много нового и интересного об истории математики в этих странах.