Преобразование в плоскости. Методика изучения симметрии в начальной школе

Цели:
развитие логического мышления и пространственного воображения детей;
формировать умения узнавать геометрические фигуры и их части;
изображать фигуры на чертеже.

Задачи:
развитие пространственного воображения у ребенка, умения наблюдать, сравнивать, обобщать, анализировать и абстрагировать
формирование у ребенка практических умений измерения и построения геометрических фигур с помощью циркуля, угольника и линейки

Программа Л.Г. Петерсон предусматривает большой объем геометрического материала (особенно в 4-ом классе)

И целями геометрической линии Петерсон является:
1. Формирование представлений о геометрических фигурах и отношениях;
2. Формирование умения изображать геометрические фигуры с помощью чертежных инструментов;
3. Развитие вербально – логического мышления, математической речи;
4. Подготовка к изучению геометрии в средней школе.

Геометрическое преобразование плоскости - взаимно-однозначное отображение этой плоскости на себя.
В курсе математики Л.Г. Петерсон сохраняется преемственность с традиционной программой по математике, но усиливается геометрическое содержание за счет большого дополнительного материала (особенно в 4-ом классе), что позволяет расширить геометрические представления и знания учащихся, развивать их пространственное воображение, техническое и логическое мышление, конструкторские умения

Возникает вопрос: доступен ли этот материал для детей младшего школьного возраста?
Конечно, да.
Учащиеся знакомятся с плоскими фигурами: треугольником, прямоугольником, квадратом, ромбом и др.;

задания № 2–4, стр. 37 предназначены для этапа первичного закрепления. В № 2 ученики должны выразить в речи выполняемые преобразования. Можно сказать им, что направление и расстояние, на которое осуществляется перенос, удобно показывать направленным отрезком (вектором), и попросить нарисовать направленные отрезки, соответствующие данным преобразованиям. Так, в задании (а) горизонтальный вектор означает, что фигура переносится на 7 клеток вправо, а вертикальный – что она переносится на 4 клетки вниз; в задании (б) горизонтальный вектор показывает, что фигура переносится на 6 клеток влево, а вертикальный – что она переносится на 5 клеток вверх:

В процессе выполнения заданий на преобразование фигур формируется умение работать с циркулем и линейкой. Если позволит время, можно предложить детям придумать свои преобразования и выполнить несколько из них. В завершение целесообразно обратить внимание учащихся на то, что преобразования фигур часто используются при составлении узоров, показать им несколько узоров, полученных в результате переноса некоторого рисунка, предложить нарисовать свой узор.

Вводится тема «Преобразование фигур» в 3 классе по программе «Школа 2000» Л.Г.Петерсон

Виды симметрии:
Центральная симметрия
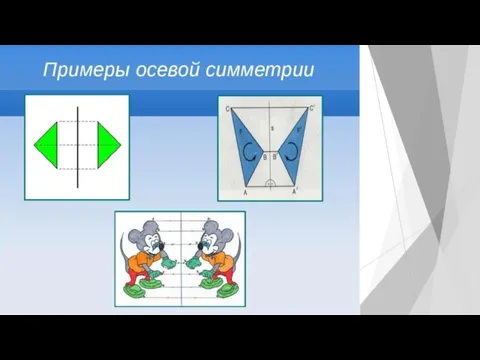
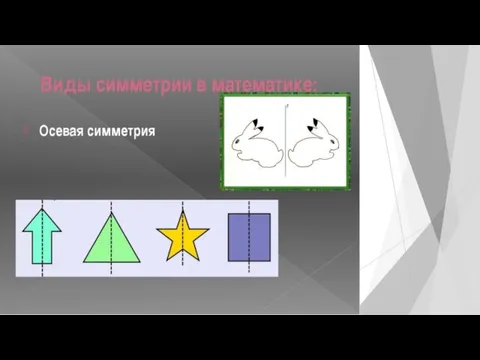
Осевая симметрия
Зеркальная симметрия

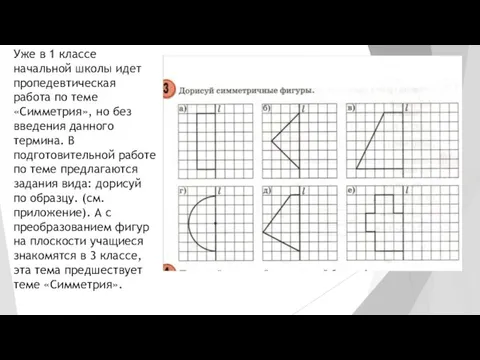
Уже в 1 классе начальной школы идет пропедевтическая работа по теме «Симметрия», но без введения данного термина. В подготовительной работе по теме предлагаются задания вида: дорисуй по образцу. (см. приложение). А с преобразованием фигур на плоскости учащиеся знакомятся в 3 классе, эта тема предшествует теме «Симметрия».

Если сверху посмотреть на любое насекомое и мысленно провести посередине прямую (плоскость), то левые и правые половинки насекомых будут одинаковыми и по расположению, и по размерам, и по окраске. Ведь мы ни разу не видели, чтобы у жука или стрекозы, у любого другого насекомого лапы слева были бы ближе к голове, чем справа, а правое крыло бабочки или божьей коровки было бы больше, чем левое. Такого в природе не бывает, иначе бы насекомые не смогли бы летать.

На уроках учащиеся выполняют практические действия с фигурами на клетчатой бумаге, в процессе которых их представление о преобразовании фигур уточняются. Понятие «преобразование фигур» можно пояснить, как перемещение фигур на плоскости, их перенос. На 14 уроке рассматривается перенос фигур на данное число клеток вверх, вниз, направо и налево .

В окружающем мире дети могут наблюдать симметрию достаточно часто: симметрично расположены глаза и уши человека, дверцы стенного шкафа и т.д.

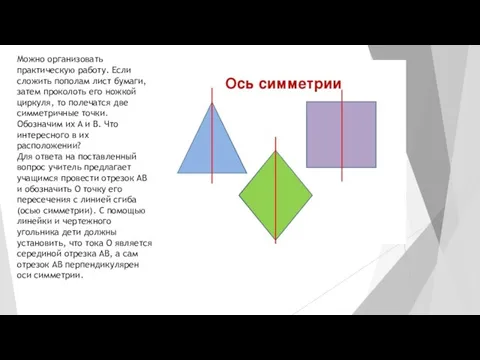
Можно организовать практическую работу. Если сложить пополам лист бумаги, затем проколоть его ножкой циркуля, то полечатся две симметричные точки. Обозначим их A и B. Что интересного в их расположении?
Для ответа на поставленный вопрос учитель предлагает учащимся провести отрезок AB и обозначить О точку его пересечения с линией сгиба (осью симметрии). С помощью линейки и чертежного угольника дети должны установить, что тока О является серединой отрезка AB, а сам отрезок АВ перпендикулярен оси симметрии.

В процессе выполнения задания на преобразование фигур и на построение симметричных фигур формируется умение работать с циркулем, чертежным угольником и линейкой.

Зеркальная симметрия

Переносная симметрия

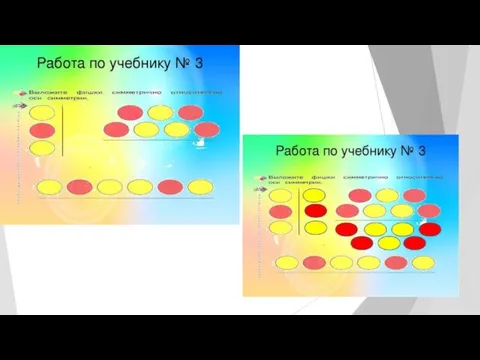
Задания на симметрию по программе «школа 2000» Л.Г. Петерсон

Так же есть задания в рабочей тетраде

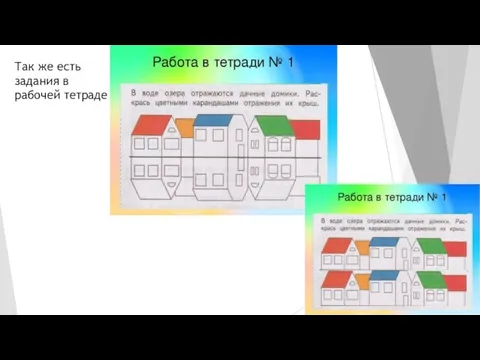
Задания на логику на тему «Симметрия»

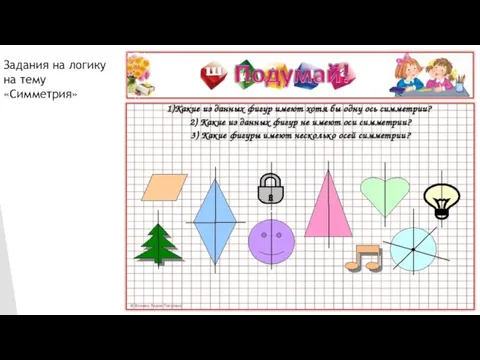
Вводится тема «Симметрия»
3 класс Л.Г. Петерсон

Дорисуй вторую половинку и раскрась

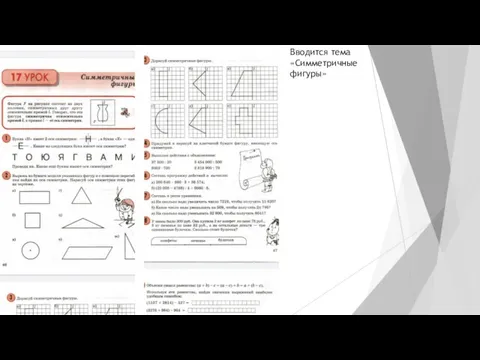
Вводится тема «Симметричные фигуры»