Понятие Марковского случайного процесса

ПОНЯТИЕ «Марковский случайный процесс»
Случайный процесс, протекающий в системе S с дискретными состояниями s1, s2, …, si, …, называется марковским, если для любого момента времени t0 вероятность каждого из состояний системы в будущем (при t > t0), зависит только от ее состояния в настоящем (при t = t0), и не зависит от того, как система пришла в это состояние, т.е. не зависит от ее поведения в прошлом (при t < t0).

ПРИМЕР 1 «Марковский случайный процесс»
Система S – счетчик в такси. Состояние системы в момент t характеризуется количеством километров, пройденных автомобилем до данного момента. Пусть в момент t0 счетчик показывает S0. Вероятность того, что в момент t >t0 счетчик покажет то или иное количество километров (точнее, соответствующее количество денег) S1, зависит только от S0, но не зависит от того, в какие моменты времени изменялись показания счетчика до момента t0.

ПРИМЕР 2 «Марковский случайный процесс»
Система S – группа шахматных фигур. Состояние системы характеризуется числом фигур противника, сохранившимися на доске в момент t0. Вероятность того, что в момент t >t0 перевес будет на стороне одного из игроков, зависит в первую очередь от того, в каком состоянии система находится в данный момент t0, а не от того, когда и в какой последовательности исчезли фигуры с доски до момента t0.

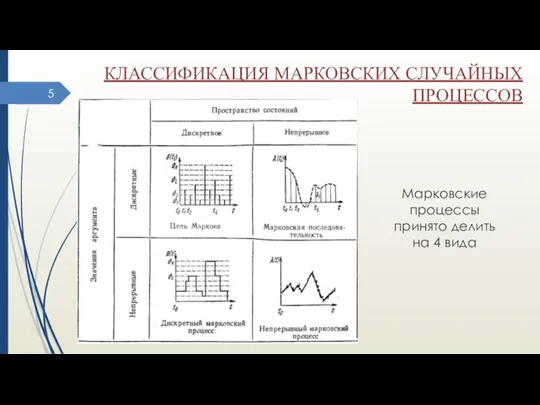
КЛАССИФИКАЦИЯ МАРКОВСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Марковские процессы принято делить на 4 вида

КЛАССИФИКАЦИЯ МАРКОВСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Поскольку модели массового обслуживания относятся к классу дискретных систем, то в дальнейшем будут рассматриваться только случайные процессы с дискретными состояниями.
Марковская цепь – процесс, состояния которого дискретны (т.е. их можно перенумеровать), и время, по которому он рассматривается, также дискретно (т.е. процесс может менять свои состояния только в определенные моменты времени). Такой процесс идет (изменяется) по шагам (иначе - по тактам).
Например: Число пассажиров в транспорте только в определенные моменты времени (на остановках).

КЛАССИФИКАЦИЯ МАРКОВСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Дискретный марковский процесс – множество состояний дискретно (можно перечислить), а время непрерывно (переход из одного состояния в другое – в любой момент времени).
У непрерывных процессов между двумя состояниями мы можем найти промежуточное.
Например: Число абонентов телефонной станции говорящих по телефону.

ПРИМЕР МОДЕЛИРОВАНИЯ МАРКОВСКИХ ПРОЦЕССОВ
Пример.
Рассмотрим систему обладающую тремя состояниями и предназначенную для моделирования погоды. Предполагается, что раз в день (например, в полдень) состояние погоды описывается одной из следующих характеристик:
S1– осадки, S2 – облачно, S3– ясно.
Матрица переходных вероятностей дана и имеет вид :

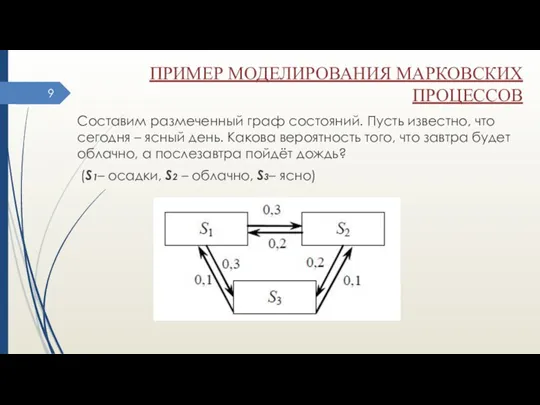
ПРИМЕР МОДЕЛИРОВАНИЯ МАРКОВСКИХ ПРОЦЕССОВ
Составим размеченный граф состояний. Пусть известно, что сегодня – ясный день. Какова вероятность того, что завтра будет облачно, а послезавтра пойдёт дождь?
(S1– осадки, S2 – облачно, S3– ясно)

ПРИМЕР МОДЕЛИРОВАНИЯ МАРКОВСКИХ ПРОЦЕССОВ
Вероятность того, что завтра будет облачно, а послезавтра пойдёт дождь, находим по закону умножения вероятностей зависимых событий:
Поставим другой вопрос: какова вероятность того, что погода останется в некотором известном состоянии Si ровно Х дней?
Например, если известно, что сегодня дождь, то вероятность того, что он будет идти ровно 3 дня (включая сегодняшний), равна:
(1)
(2)

ПРИМЕР МОДЕЛИРОВАНИЯ МАРКОВСКИХ ПРОЦЕССОВ
Математическое ожидание случайной величины X можно рассматривать как характеристику длительности данного состояния Si в цепи Маркова. Для геометрического распределения можно получить:
(3)

ВЫВОДЫ
С помощью моделирования Марковского процесса имеется возможность прогнозирования погодных условий.
Так было выявлено, что:
Вероятность того, что завтра будет облачно, а послезавтра пойдёт дождь равна – 0,02;
Вероятность того, что дождь будет идти ровно 3 дня равна – 0,096;
Среднее число дождливых дней подряд оказывается равным – 1,67 формула (3);
Среднее число облачных дней – 2,5 формула (3);
Среднее число ясных дней – 5 формула (3);