Решение уравнений и неравенств, содержащих параметр, с использованием параллельного переноса вдоль оси Oy

Уравнения (неравенства) вида ,
где функция задает семейство прямых,
параллельных оси
Требования этих задач содержат слова: «при каких
значениях параметра уравнение (неравенство) имеет
заданное количество корней»
Изучите следующий теоретический материал:
Название группы уравнений (неравенств)
Отличительный признак данной группы задач

Выберите уравнения (неравенства), которые относятся к группе уравнений (неравенств) вида , где
функция задает семейство прямых, параллельных оси :
При каких значениях уравнение имеет
единственное решение?
При каких значениях уравнение имеет
единственное решение?
3) Сколько решений в зависимости от параметра имеет уравнение
?
4) При каких значениях неравенство имеет
решение?
1; 4
1; 2
3; 4
2; 3

Изучите алгоритм решения
Привести уравнение (неравенство) к виду
, где функция задает семейство прямых.
2. Построить график функции .
3. Построить график функции , где .
4. Осуществляя параллельный перенос построенной
прямой, найти ситуацию, отвечающую требованию
задачи.
5. Ответить на вопрос задачи.

Изучите пример решения задания: При каких значениях параметра
уравнение имеет ровно три корня?
Решение.
1. Приводим уравнение к виду , где функция
задает семейство прямых: .
2. Строим график функции .
3. Строим график функции , где .
4. Осуществляя параллельный перенос построенной прямой,
находим ситуацию, отвечающую требованию задачи: при каких
значениях параметра уравнение имеет ровно три корня?
Уравнение имеет ровно три корня в двух случаях: если прямая проходит
через точку и если прямая проходит через точку .
5. Отвечаем на вопрос задачи: уравнение имеет ровно три корня
при и при .
Ответ: -1; -0,5.

Решите задачу
При каких значениях уравнение имеет
единственное решение?
Первый шаг алгоритма
Приводим уравнение к виду ,
где функция задает семейство прямых.
а
б
в
г

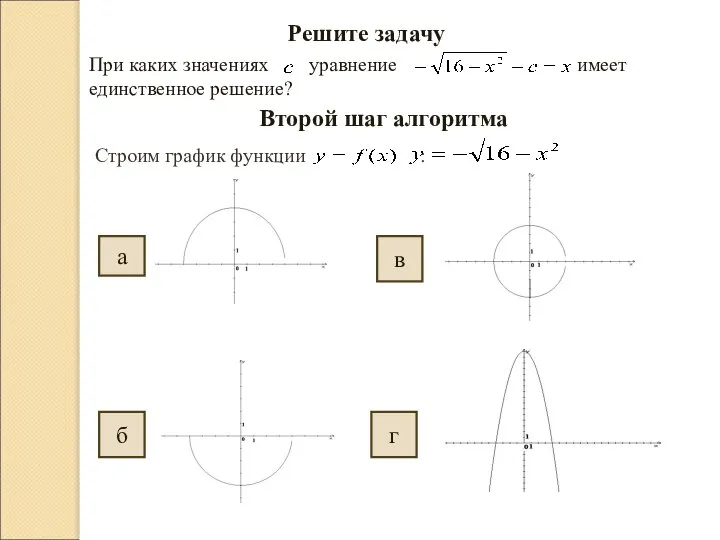
Решите задачу
При каких значениях уравнение имеет
единственное решение?
Второй шаг алгоритма
Строим график функции :
а
б
г
в

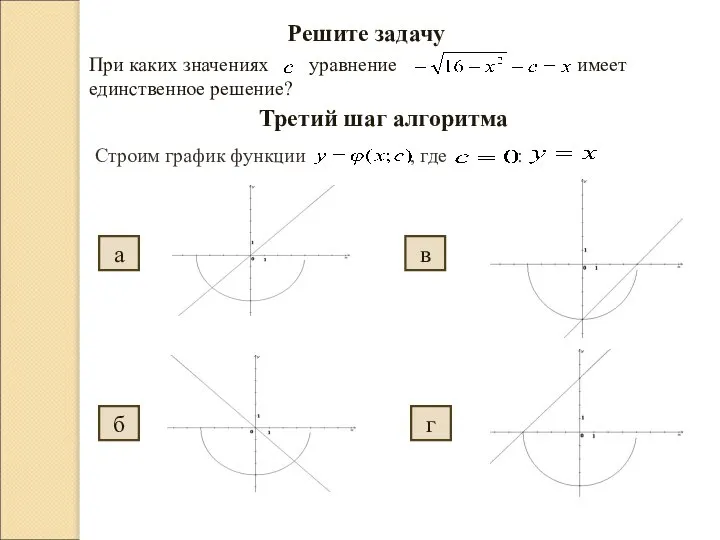
Решите задачу
При каких значениях уравнение имеет
единственное решение?
Третий шаг алгоритма
Строим график функции , где :
а
б
г
в

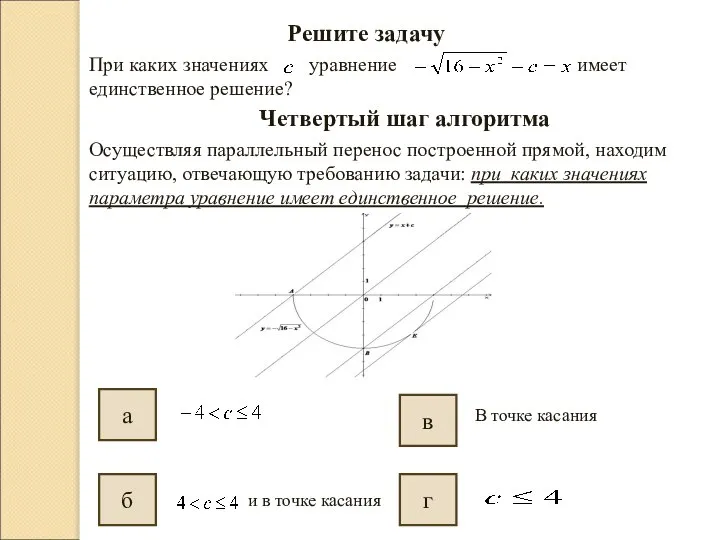
Решите задачу
При каких значениях уравнение имеет
единственное решение?
Четвертый шаг алгоритма
Осуществляя параллельный перенос построенной прямой, находим ситуацию, отвечающую требованию задачи: при каких значениях
параметра уравнение имеет единственное решение.
а
б
в
г
и в точке касания
В точке касания

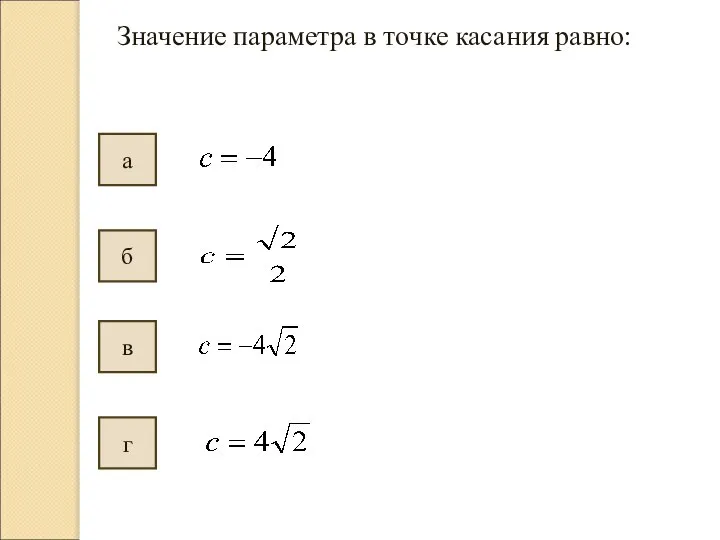
Найдите значение параметра в точке касания
по алгоритму:
Найти абсциссу точки касания прямой к
графику функции :
а) найти для функции ;
б) найти из уравнения прямой ;
в) составить уравнение и решить его.
2) Найти значение параметра , подставив в уравнение
значение .

Значение параметра в точке касания равно:
г
в
б
а

Решите задачу
При каких значениях уравнение имеет
единственное решение?
Пятый шаг алгоритма
Отвечаем на вопрос задачи: уравнение имеет единственное решение
при и при .

Прочитайте и внесите изменения в свое решение
1. Приводим уравнение к виду .
2. Строим график функции
3. Строим график функции
4. Уравнение имеет единственное решение при и в точке
касания. Найдем значение параметра в точке касания:
, ,
5. Уравнение имеет единственное решение при и при
Ответ: при и при .

Решите задачу
При каких значениях параметра неравенство имеет решение?
Проверить

При каких значениях параметра неравенство имеет решение?
Решение.
1. Приводим неравенство к виду .
2. Строим график функции
3. Строим график функции
4. Неравенство имеет решение при значениях параметра , в которых прямая
лежит ниже прямой, проходящей через точку касания.
Найдем значение параметра в точке касания:
5. Неравенство имеет решение при .
Ответ: при .
Верно
Неверно