Содержание
- 2. Повторим Окружность – это множество точек плоскости, равноудаленных от данной точки. Эта точка называется центром окружности.
- 3. Повторим Окружность – это множество точек плоскости, равноудаленных от данной точки. Эта точка называется центром окружности.
- 4. Случаи взаимного расположения прямой и окружности dd d dd d =d = d = r dd
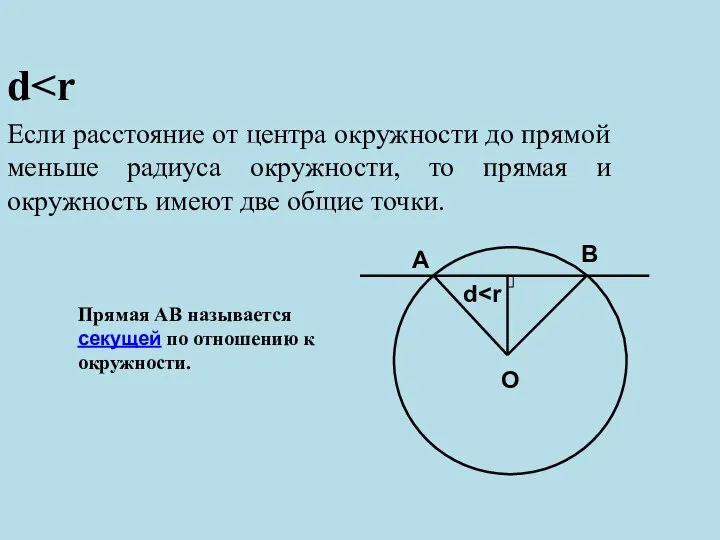
- 5. d Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют
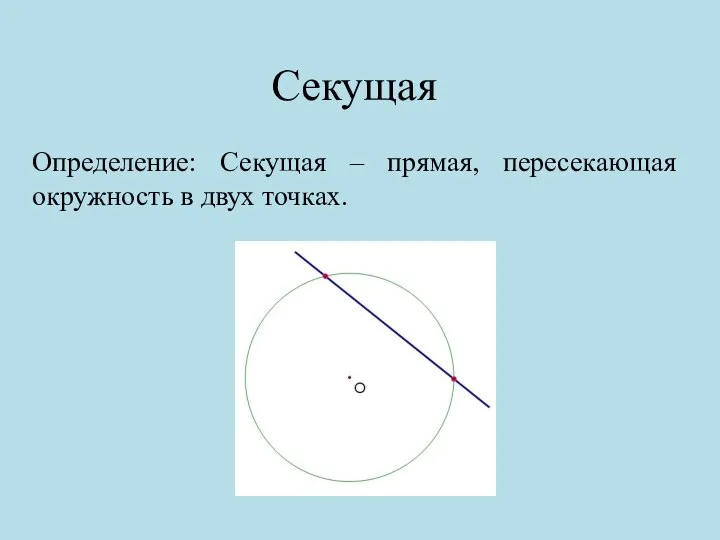
- 6. Секущая Определение: Секущая – прямая, пересекающая окружность в двух точках.
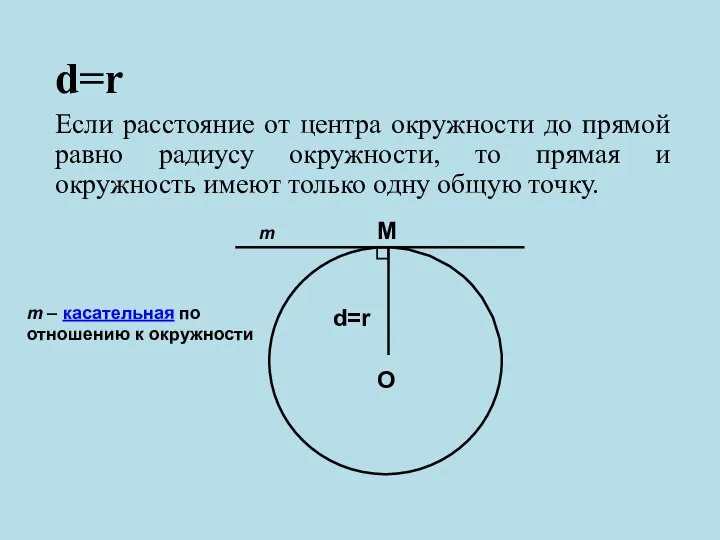
- 7. d=r Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют
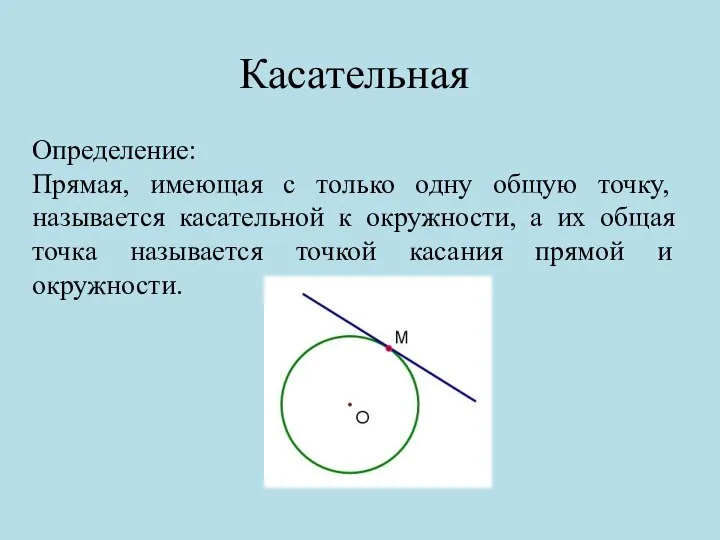
- 8. Касательная Определение: Прямая, имеющая с только одну общую точку, называется касательной к окружности, а их общая
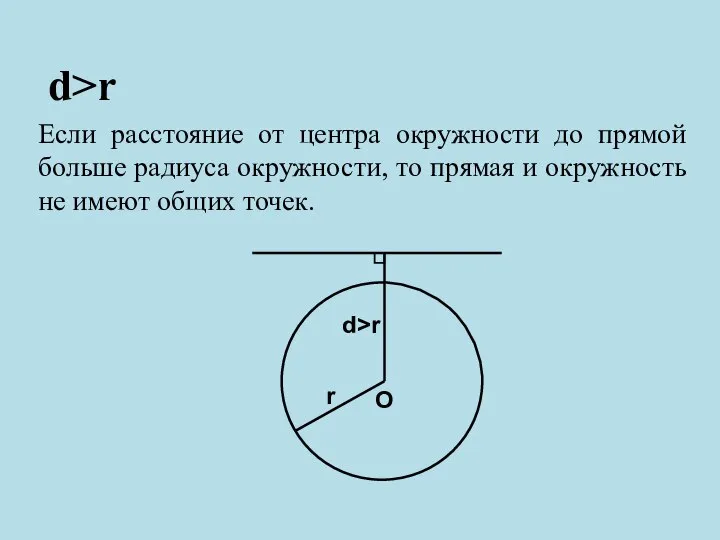
- 9. d>r Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не
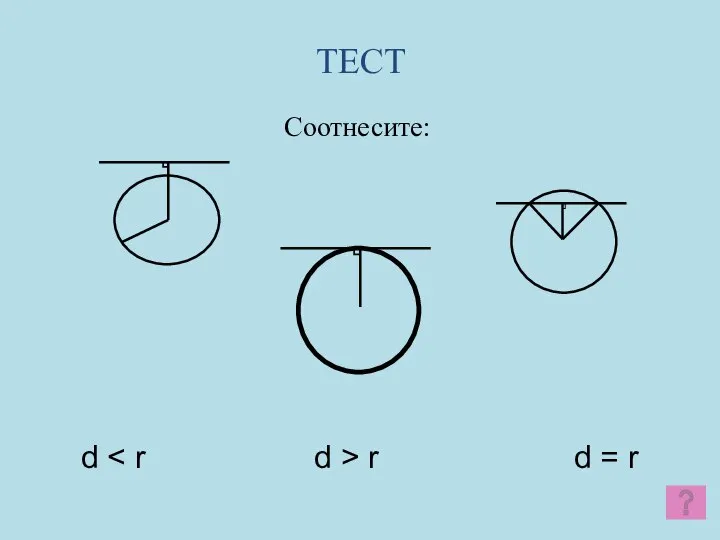
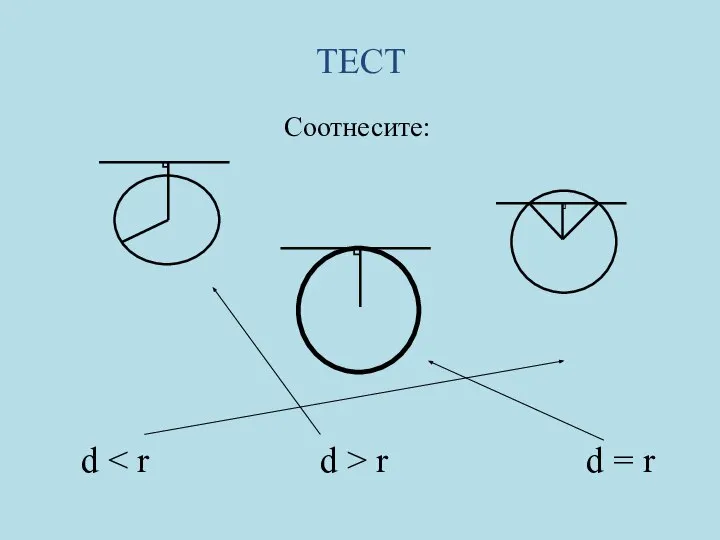
- 10. ТЕСТ Соотнесите: d r d = r
- 11. ТЕСТ Соотнесите: d r d = r
- 12. Пример 1. Пусть d – расстояние от центра окружности радиуса r до прямой m. Определи, каково
- 13. Радиус окружности равен 6 см. Каким может быть расстояние от центра окружности до прямой a, чтобы
- 14. Радиус окружности равен 11 см. Каким может быть расстояние от центра окружности до прямой a, чтобы
- 15. Пусть d – расстояние от центра окружности радиуса r до прямой p. Определи, каково будет взаимное
- 16. Пусть d – расстояние от центра окружности радиуса r до прямой p. Определи, каково будет взаимное
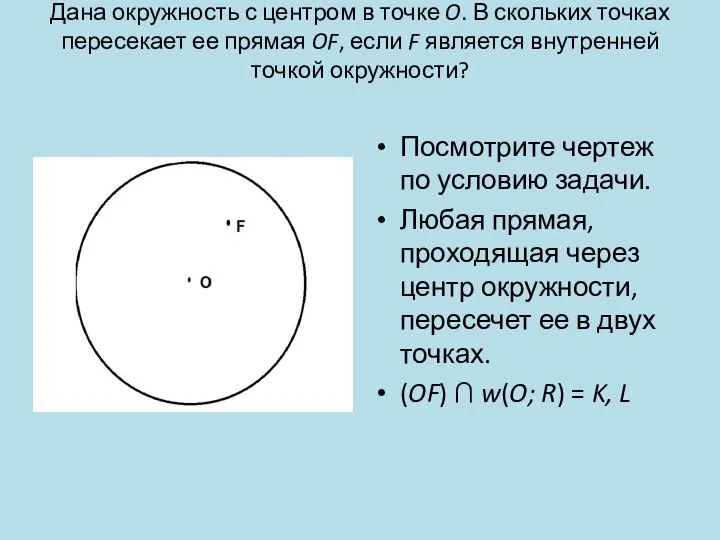
- 17. Дана окружность с центром в точке O. В скольких точках пересекает ее прямая OF, если F
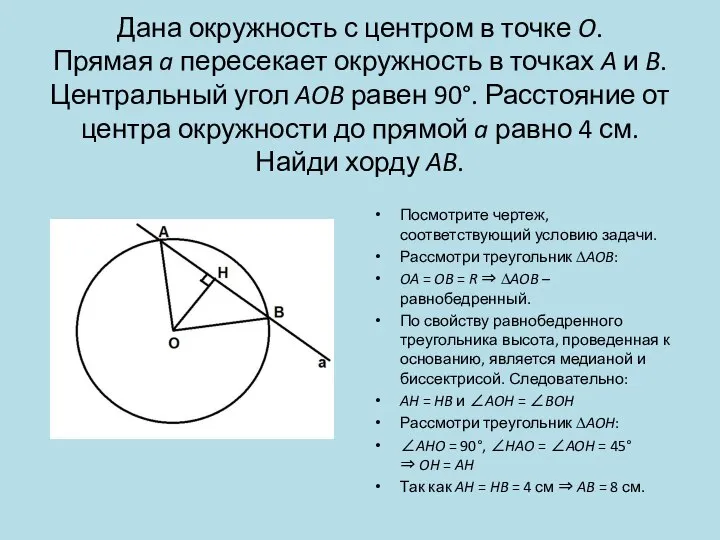
- 18. Дана окружность с центром в точке O. Прямая a пересекает окружность в точках A и B.
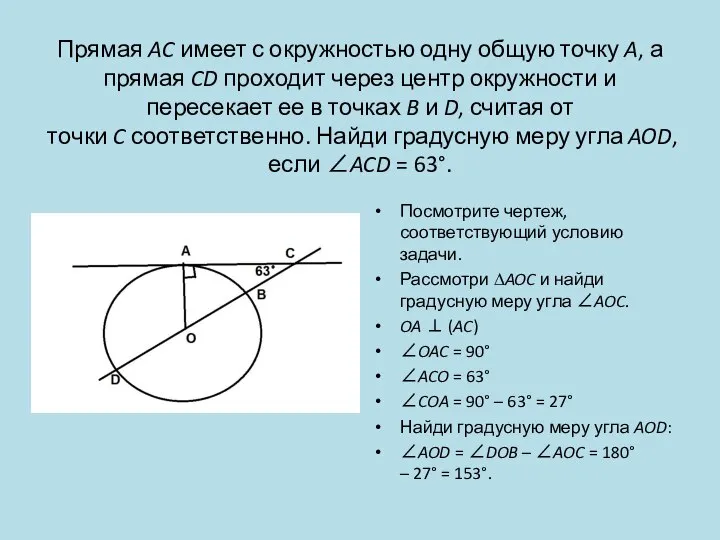
- 19. Прямая AC имеет с окружностью одну общую точку A, а прямая CD проходит через центр окружности
- 20. Учебные задания 1. Радиус окружности равен 10 см. Каким может быть расстояние от центра окружности до
- 22. Скачать презентацию









 Квадратный корень из степени
Квадратный корень из степени Определение свойств функции по графику
Определение свойств функции по графику Параллельные прямые, перпендикулярные к плоскости
Параллельные прямые, перпендикулярные к плоскости Основы математической статистики. Регрессионный и корреляционный анализы
Основы математической статистики. Регрессионный и корреляционный анализы Задача о кратчайшем пути
Задача о кратчайшем пути Развертка. Создание объёмных фигур из плоскости
Развертка. Создание объёмных фигур из плоскости Перетворення графіків
Перетворення графіків Идеально сбалансированное дерево. Задание
Идеально сбалансированное дерево. Задание Больше, меньше, столько же
Больше, меньше, столько же Геометрические тела. Обьём прямоугольного параллелепипеда. 5 класс
Геометрические тела. Обьём прямоугольного параллелепипеда. 5 класс Формирование действия моделирования через решение текстовых задач
Формирование действия моделирования через решение текстовых задач Уравнение окружности и прямой
Уравнение окружности и прямой Мир чисел
Мир чисел Симмертия. Зеркальное отражение – симметрия
Симмертия. Зеркальное отражение – симметрия Деление дробей
Деление дробей Соста числа 11
Соста числа 11 Деление десятичных дробей
Деление десятичных дробей Квадрат. Основные свойства квадрата
Квадрат. Основные свойства квадрата Сравнение и измерение отрезков
Сравнение и измерение отрезков Стандартный вид одночлена
Стандартный вид одночлена Презентация на тему Решение иррациональных неравенств (11 класс)
Презентация на тему Решение иррациональных неравенств (11 класс)  Презентация на тему КВАДРАТИЧНАЯ ФУНКЦИЯ И КВАДРАТИЧНЫЕ НЕРАВЕНСТВА
Презентация на тему КВАДРАТИЧНАЯ ФУНКЦИЯ И КВАДРАТИЧНЫЕ НЕРАВЕНСТВА  Домашнее задание по геометрии
Домашнее задание по геометрии Количество делителей числа
Количество делителей числа Комплексные числа
Комплексные числа Цифра 1. Посчитаем до 10
Цифра 1. Посчитаем до 10 Презентация по математике "Алгоритмы внутренних точек с приближенным решением вспомогательной задачи" -
Презентация по математике "Алгоритмы внутренних точек с приближенным решением вспомогательной задачи" -  Algorytmy i struktury danych
Algorytmy i struktury danych