Содержание
- 2. Неизвестные величины принято обозначать последними буквами латинского алфавита (х, у, z,…), параметры – первыми буквами (а,
- 3. Примеры возвратных уравнений а) 7х³-2х²-2х+7=0; б) 5х³-3х²-3х+5=0; в) 12х⁴-7х³+2х²-7х+12=0; г) 2х⁴+8х³-4х²+8х+2=0; д) 6х⁵-7х⁴+2х³+2х²-7х+6=0.
- 4. Выполним группировку первого и последнего, второго и третьего членов уравнения, получим: (7х³+7)-2х (х+1)=0 ; 7(х+1)(х²-х+1)-2х(х+1)=0; вынесем
- 5. Пример 2 Решим возвратное уравнение
- 6. Неизвестные величины принято обозначать последними буквами латинского алфавита (х, у, z,…), параметры – первыми буквами (а,
- 7. Решить уравнение с параметром – значит для каждого значения параметра найти множество всех корней данного уравнения
- 8. Пример 3. Решить уравнение ax = 1. Решение. 1. если a ≠ 0: 2. если a
- 9. Пример 4. Решить уравнение a2x – 1 = x + a. Решение. a2x – 1 =
- 10. Решение. ОДЗ: х – 4 ≠ 0; х ≠ 4; х – 2а = 0; х
- 12. Скачать презентацию









 Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения Степень с натуральным показателем
Степень с натуральным показателем Методы решения творческих задач
Методы решения творческих задач Элементы комбинаторики. Перестановки
Элементы комбинаторики. Перестановки Деление дробных чисел
Деление дробных чисел Многогранники. Понятие многогранника. Призма
Многогранники. Понятие многогранника. Призма Действия с обыкновенными дробями. Подготовка к ОГЭ задания первой части 1, 3, 8
Действия с обыкновенными дробями. Подготовка к ОГЭ задания первой части 1, 3, 8 Правильные многогранники
Правильные многогранники Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Фракталы
Фракталы Косинусоида. Задание № 9
Косинусоида. Задание № 9 Степень с рациональным показателем. Преобразование выражений, содержащих степень с рациональным показателем
Степень с рациональным показателем. Преобразование выражений, содержащих степень с рациональным показателем Геометрическая прогрессия
Геометрическая прогрессия Путешествие в страну Геометрию
Путешествие в страну Геометрию Презентация на тему Векторы в пространстве
Презентация на тему Векторы в пространстве  Признаки существования предела
Признаки существования предела Основные геометрические фигуры
Основные геометрические фигуры Решение задач с использованием теоремы о накрест лежащих углах
Решение задач с использованием теоремы о накрест лежащих углах Бесконечные периодические десятичные дроби
Бесконечные периодические десятичные дроби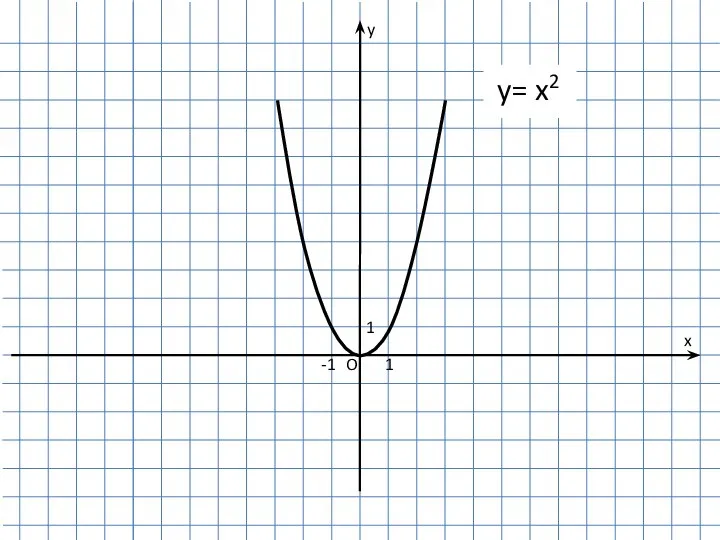 Преобразование графиков функции
Преобразование графиков функции Nepreryvnost_funktsii (1)
Nepreryvnost_funktsii (1) Вариационные ряды
Вариационные ряды Тренировочные варианты
Тренировочные варианты Окружность и длина окружности
Окружность и длина окружности Вычитание в пределах 20
Вычитание в пределах 20 Параллельные прямые в пространстве
Параллельные прямые в пространстве Введение в геометрию
Введение в геометрию Фалес Милетский - один из первых геометров
Фалес Милетский - один из первых геометров