Содержание
- 2. Если векторы a и b коллинеарны и a ≠ 0, то существует такое число k, что
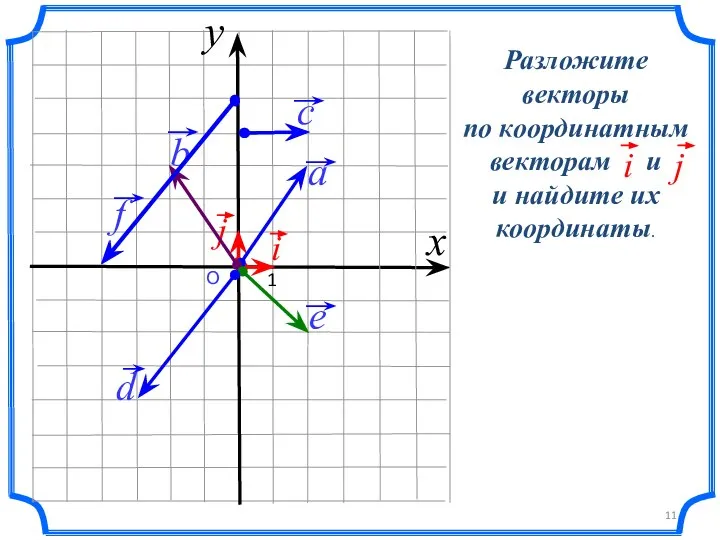
- 3. В прямоугольной системе координат отложим от точки О единичные векторы i и j Векторы i и
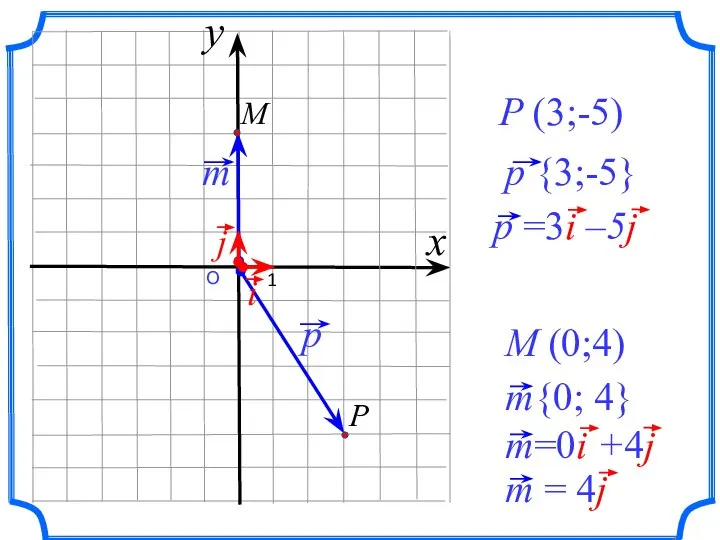
- 4. О 1 P (3;-5) M (0;4) x y
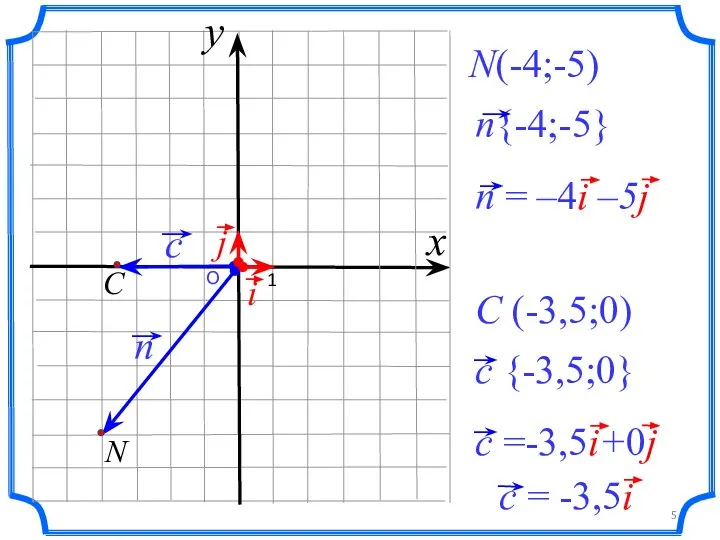
- 5. О 1 N(-4;-5) C (-3,5;0) x y
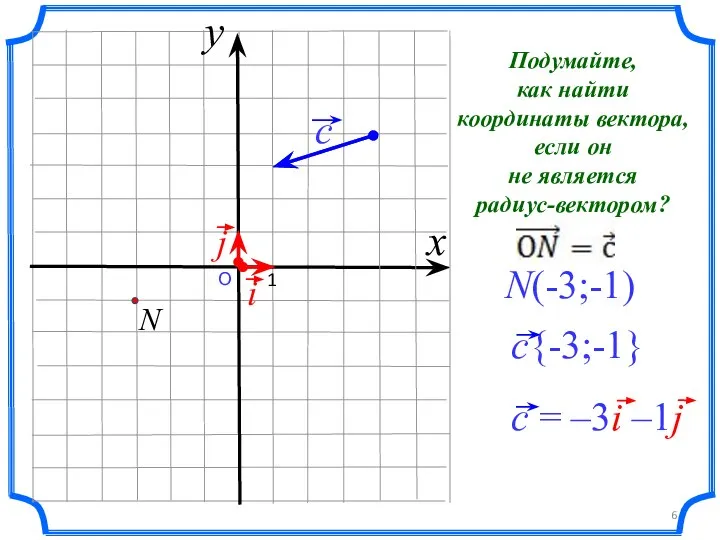
- 6. О 1 N(-3;-1) x y Подумайте, как найти координаты вектора, если он не является радиус-вектором?
- 7. Свойства: Если векторы a = xi + yj и b = ki + lj равны, то
- 8. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. Пример: Найти
- 9. ? ? ? ? ? ? ? ?
- 11. О 1 x y
- 13. Скачать презентацию





 Презентация на тему Квадратные уравнения 8 класс
Презентация на тему Квадратные уравнения 8 класс  Сложение однозначных чисел с переходом через десяток вида +8, +9 (часть 1)
Сложение однозначных чисел с переходом через десяток вида +8, +9 (часть 1) Прямые измерения, косвенные, совокупные и совместные
Прямые измерения, косвенные, совокупные и совместные 9
9 Методы и приемы реализации математических моделей теплотехнических систем макроуровня (продолжение)
Методы и приемы реализации математических моделей теплотехнических систем макроуровня (продолжение) Выделение целой части из неправильной дроби и представление смешанной дроби в виде неправильной
Выделение целой части из неправильной дроби и представление смешанной дроби в виде неправильной Задача сетевого планирования с вложением средств
Задача сетевого планирования с вложением средств Презентация на тему Простые и составные числа
Презентация на тему Простые и составные числа  Уравнение сферы
Уравнение сферы Площадь треугольника
Площадь треугольника 6. СЛАУ. Методы решения (1)
6. СЛАУ. Методы решения (1) Операции над матрицами
Операции над матрицами Устный счет
Устный счет Числа-гиганты. Из истории чисел - гигантов
Числа-гиганты. Из истории чисел - гигантов Степенная функция
Степенная функция Логарифмы. Задание
Логарифмы. Задание Сложение и вычитание в пределах 100
Сложение и вычитание в пределах 100 Логика и математическая логика. История логики. Алгебра высказываний
Логика и математическая логика. История логики. Алгебра высказываний Вычисление углов между прямыми и плоскостями
Вычисление углов между прямыми и плоскостями Действие с дробями. Устная работа
Действие с дробями. Устная работа П 3
П 3 Игра - путешествие В стране занимательной математики
Игра - путешествие В стране занимательной математики Матрицы и действия над ними
Матрицы и действия над ними Презентация на тему Цилиндр (11 класс)
Презентация на тему Цилиндр (11 класс)  Векторы. Задачи
Векторы. Задачи Тема: Письменное умножение на двузначное число. Закрепление.
Тема: Письменное умножение на двузначное число. Закрепление.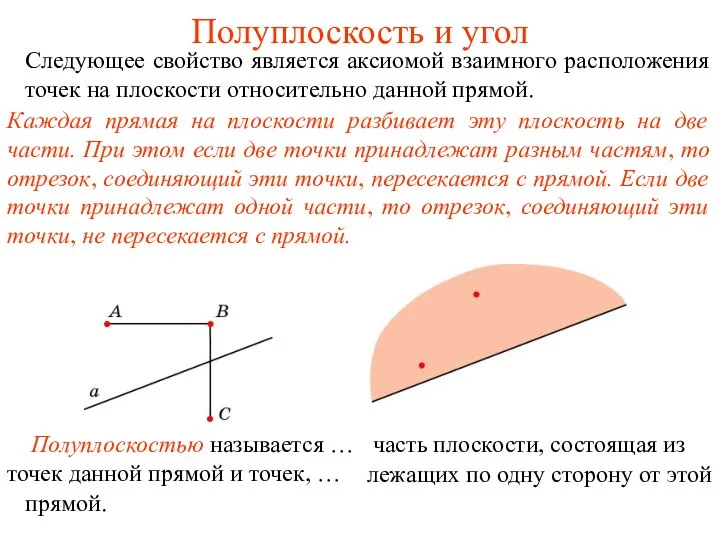 Полуплоскость и угол
Полуплоскость и угол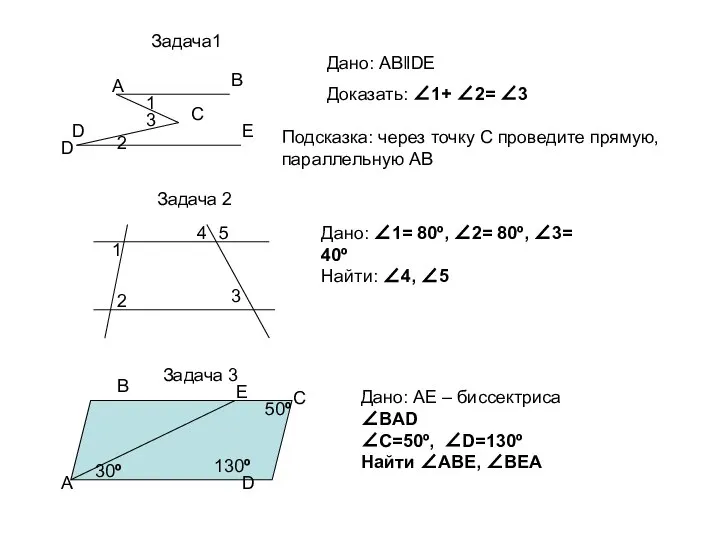 Параллельные прямые (тест)
Параллельные прямые (тест)