Содержание
- 2. Пример№1. Родители измеряли рост дочери каждые два года от 2 до 12 лет. Результаты своих измерений
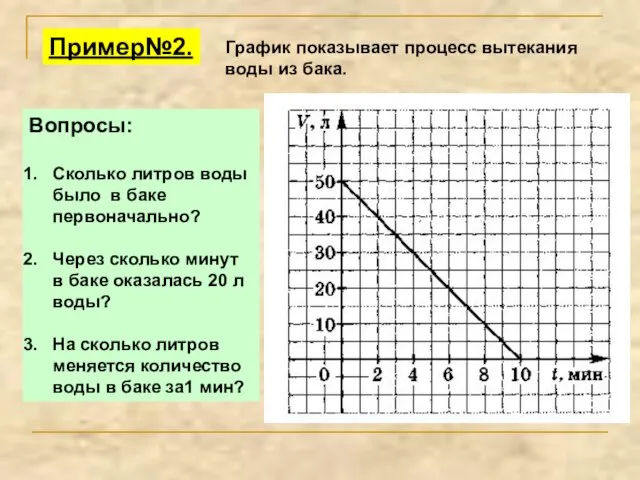
- 3. Пример№2. Вопросы: Сколько литров воды было в баке первоначально? Через сколько минут в баке оказалась 20
- 4. Вопрос: Что общее присутствовало в ранее рассмотренных примерах? Ответ: Общее: 1). Рассмотрены две взаимосвязанные величины; 2).
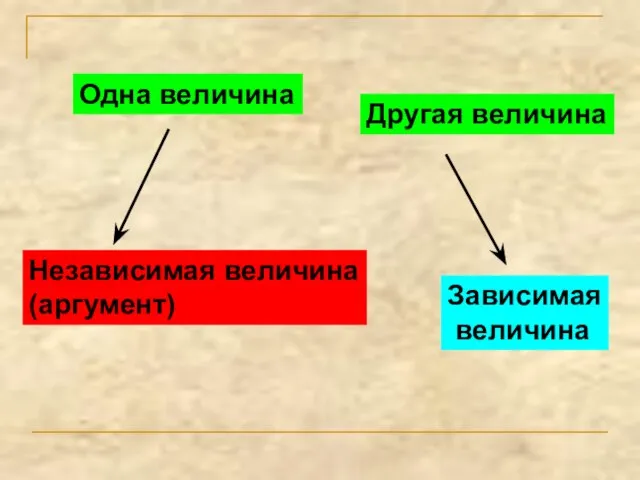
- 5. Одна величина Другая величина Независимая величина (аргумент) Зависимая величина
- 6. Пример №3. Дана формула перевода температуры, измеренной в градусах Цельсия, в градусы Фаренгейта: F=9/5 C+32, где
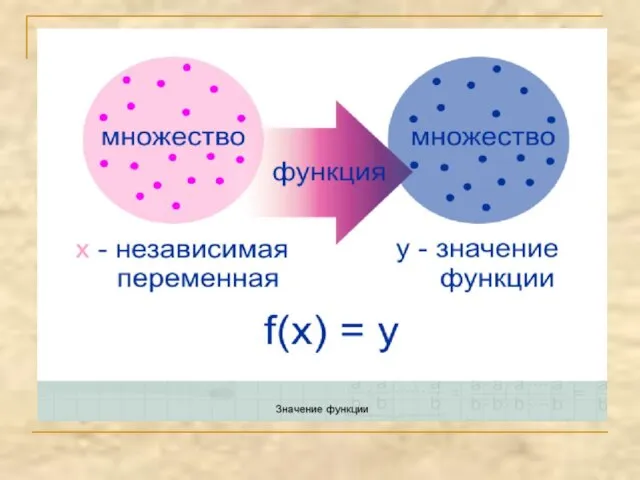
- 9. Переменную y называют функцией переменной x, если каждому значению x из некоторого числового множества соответствует одно
- 10. Функцией часто называют зависимость между двумя величинами, а также правило, по которому устанавливается соответствие между значениями
- 11. Правило, по которому по данному значению аргумента находят соответствующее значение функции, принято обозначать какой-либо буквой, чаще
- 19. Дана функция y=f (x). Используя функциональную символику, запишите следующие утверждения: А) если значение аргумента равно -2,
- 20. Дана функция f (x) = x³+x. Найдите : а) f(-3) б) f(-2) в) f(-4) г)f(5) Образец:
- 21. Проверь себя: Б) f(-2)=(-2)³+(-2)=-8+(-2)=-10 В) f(-4)=(-4)³+(-4)=-64+(-4)=-68 Г) f(5)=5³+5=125+5=130
- 22. Задание№3. Найти значение аргумента, при котором: а)функция y=2x-1 принимает значение, равное 5; б)функция y=x²+5x принимает значение,
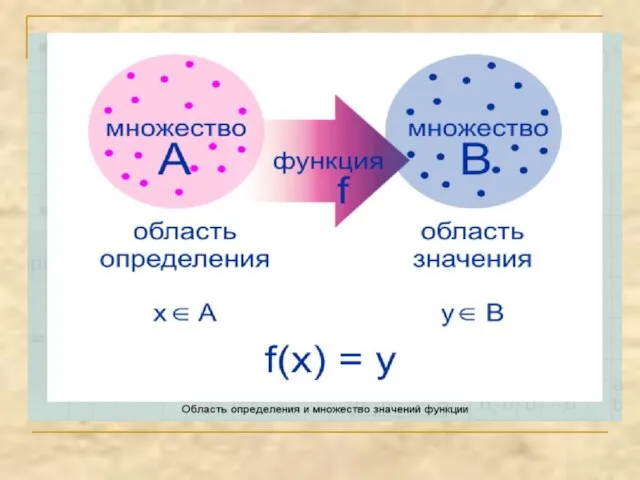
- 23. Найти область определения функции, заданной формулой: Задание№4.
- 25. Скачать презентацию
















 Прямоугольный треугольник. Тренажер. 8 класс
Прямоугольный треугольник. Тренажер. 8 класс Презентация на тему Дифференциальные уравнения первого порядка
Презентация на тему Дифференциальные уравнения первого порядка  Метод наименьших квадратов. Ordinary Least Squares, OLS
Метод наименьших квадратов. Ordinary Least Squares, OLS Секреты квадратных уравнений
Секреты квадратных уравнений Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Умножение десятичных дробей
Умножение десятичных дробей Формула Остроградского - Гаусса
Формула Остроградского - Гаусса Декартовы координаты на плоскости (решение задач)
Декартовы координаты на плоскости (решение задач) Четырехугольники. Параллелограмм
Четырехугольники. Параллелограмм Множення десяткових дробів
Множення десяткових дробів Решение тригонометрических уравнений
Решение тригонометрических уравнений Логарифмическая функция. Свойства, график. Решение примеров
Логарифмическая функция. Свойства, график. Решение примеров Тригонометрия.обратные тригонометрические функции. Простейшие тригонометрические уравнения
Тригонометрия.обратные тригонометрические функции. Простейшие тригонометрические уравнения Изображение фигур в пространстве
Изображение фигур в пространстве Свойства квадратных корней
Свойства квадратных корней Изменение глаголов по числам
Изменение глаголов по числам Найдите значение выражения
Найдите значение выражения Параллельное проектирование. Площадь ортогональной проекции. Изображение пространственных фигур
Параллельное проектирование. Площадь ортогональной проекции. Изображение пространственных фигур Цифра 8
Цифра 8 Функция y=sin x, её свойства и график
Функция y=sin x, её свойства и график Конус – тело вращения
Конус – тело вращения Основные понятия комбинаторики. Раздел 4
Основные понятия комбинаторики. Раздел 4 Логарифмы вокруг нас
Логарифмы вокруг нас Задачи на построение
Задачи на построение Основы анализа данных. Регрессионный анализ. (Лекция 6)
Основы анализа данных. Регрессионный анализ. (Лекция 6)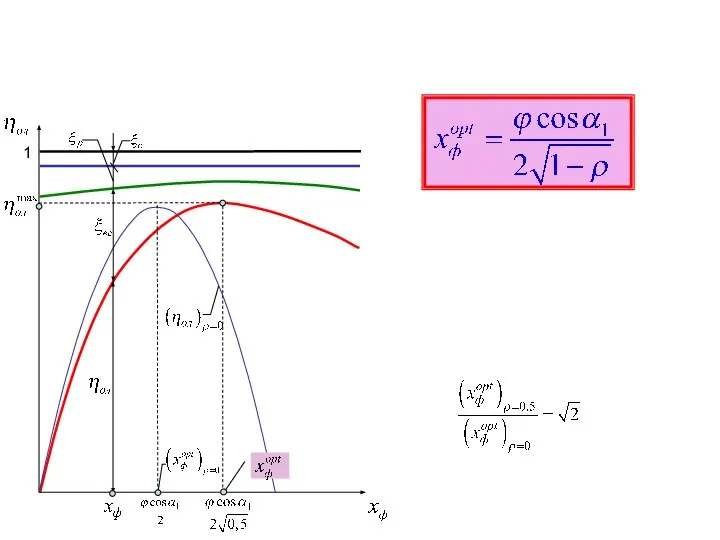 Оптимальный располагаемый теплоперепад ступени
Оптимальный располагаемый теплоперепад ступени Матрицы и действия над ними
Матрицы и действия над ними Построение сечений в тетраэдре
Построение сечений в тетраэдре