Содержание
- 2. Пример. Брошена игральная кость. Найти вероятность событий: А- выпало четное число очков, В – число выпавших
- 3. Если событие происходит обязательно (при любом элементарном исходе), то оно называется достоверным. Пример Выпадения числа очков
- 4. Если событие никогда не происходит (ни при каком элементарном исходе), то оно называется невозможным. Пример Выпадения
- 5. Вероятность любого события находится в интервале от 0 до 1.
- 6. а) выиграет 1000 рублей. б) выиграет 5000 рублей. в) выиграет 10000 рублей. г) не получит никакого
- 7. Выпущено 1500 лотерейных билетов. На 10 из них приходится выигрыш в 10000 рублей, на 100 в
- 8. Студент знает 20 из 30 вопросов к экзамену. Каждый экзаменационный билет содержит 5 вопросов. Найти вероятность
- 9. Для вычисления числа способов выбора из n элементов m Есть специальная формула
- 10. Студент знает 20 из 30 вопросов к экзамену. Каждый экзаменационный билет содержит 5 вопросов. Найти вероятность
- 11. Студент знает 20 из 30 вопросов к экзамену. Каждый экзаменационный билет содержит 5 вопросов. Найти вероятность
- 12. Студент знает 20 из 30 вопросов к экзамену. Каждый экзаменационный билет содержит 5 вопросов. Найти вероятность
- 13. Имеется 10 рекламных баннеров баннеров, которые в случайном порядке отображаются на экране, каждый в течение одной
- 15. Скачать презентацию












 Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром.
Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром. Построение сечений
Построение сечений Признаки равенства треугольников
Признаки равенства треугольников Решение систем линейных алгебраических уравнений. Тема 2
Решение систем линейных алгебраических уравнений. Тема 2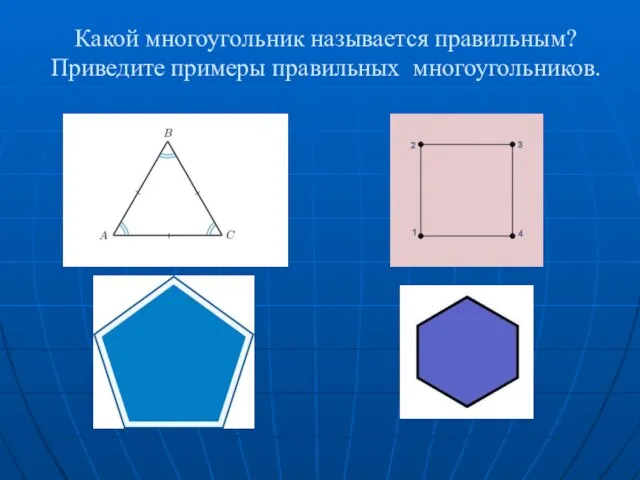 Какой многоугольник называется правильным? Приведите примеры правильных многоугольников
Какой многоугольник называется правильным? Приведите примеры правильных многоугольников Методы составления уравнений неголономной механики в задаче волнового твердотельного гироскопа
Методы составления уравнений неголономной механики в задаче волнового твердотельного гироскопа Построение сечений
Построение сечений Блок - схемы алгоритмов
Блок - схемы алгоритмов Графики
Графики Решение СЛУ
Решение СЛУ Сечение поверхностей плоскостью
Сечение поверхностей плоскостью Решение показательных уравнений. Корень уравнения
Решение показательных уравнений. Корень уравнения Пределы
Пределы Случаи сложения 470 +80 и вычитания 560-90
Случаи сложения 470 +80 и вычитания 560-90 Численные методы решения систем линейных уравнений
Численные методы решения систем линейных уравнений Комплексные корни квадратных уравнений
Комплексные корни квадратных уравнений Импорт-экспорт данных. Прикладные методы расчета и программные комплексы (5)
Импорт-экспорт данных. Прикладные методы расчета и программные комплексы (5) Геометричекие тела
Геометричекие тела Презентация на тему Математический калейдоскоп
Презентация на тему Математический калейдоскоп  Презентация на тему Умножение многочлена на многочлен
Презентация на тему Умножение многочлена на многочлен  Решение задач с пропорциональными величинами
Решение задач с пропорциональными величинами П 3
П 3 Логарифмические уравнения
Логарифмические уравнения Многогранники. Единица объема. Объем прямоугольного параллелепипеда
Многогранники. Единица объема. Объем прямоугольного параллелепипеда Функция нескольких переменных
Функция нескольких переменных Квадратичная функция
Квадратичная функция Квадратные неравенства
Квадратные неравенства Четырёхугольники. Тест
Четырёхугольники. Тест