Равнобедренный треугольник

E
В
D
1
2

F
E
D
1
2

E
P
M
1
2

C
B
A
K
D

C
B
A
K
D
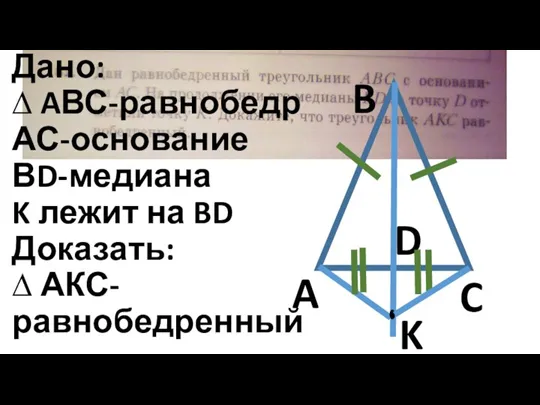
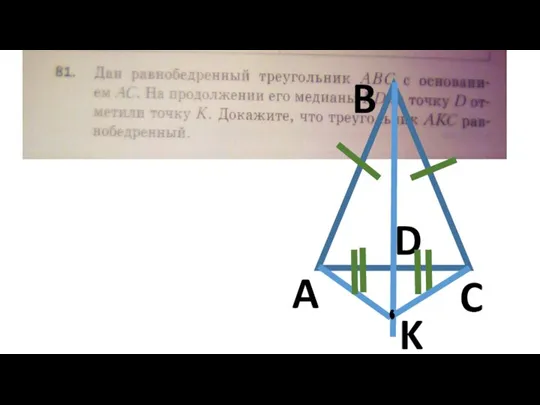
Дано:
∆ AВС-равнобедр
АС-основание
ВD-медиана
K лежит на BD
Доказать:
∆ АКС-равнобедренный

Решение:
∆ AВС-равнобедр , значит, медиана BD является высотой, тогда BD перпендикулярна АС.
Значит, в ∆ АКС КD высота.
Т.к. AD=DC, то DK-медиана в ∆ АКС. Тогда по признаку равнобедренного треугольника(медиана является высотой) имеем, что ∆ АКС-равнобедренный.
Что и требовалось доказать.

C
B
A
K
М
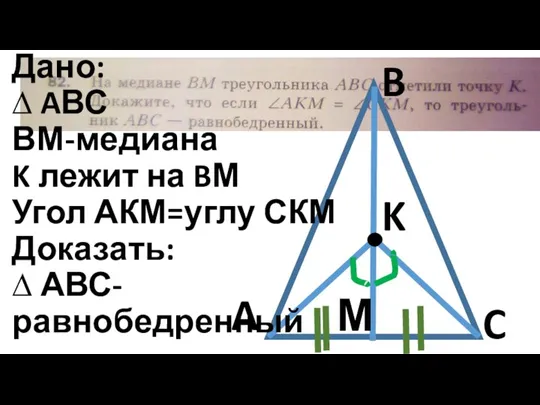
Дано:
∆ AВС
ВМ-медиана
K лежит на BМ
Угол АКМ=углу СКМ
Доказать:
∆ АВС-равнобедренный

C
B
A
K
М
Решение:
ВМ-медиана треугольника AВС, значит, АМ=МС.
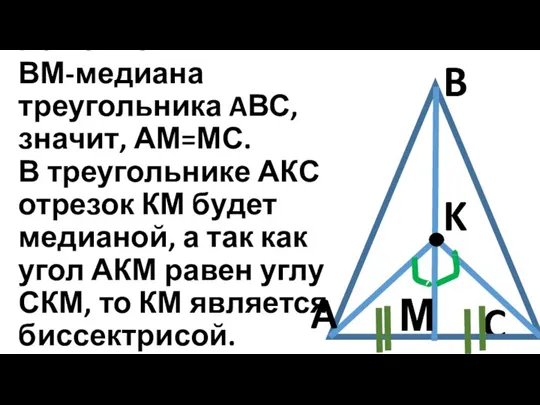
В треугольнике АКС отрезок КМ будет медианой, а так как угол АКМ равен углу СКМ, то КМ является биссектрисой.

C
B
A
K
М
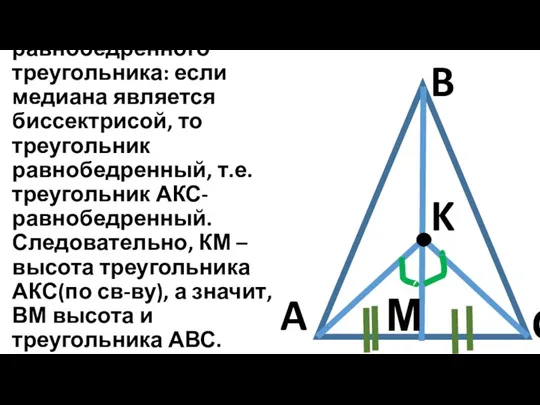
А по признаку равнобедренного треугольника: если медиана является биссектрисой, то треугольник равнобедренный, т.е. треугольник АКС-равнобедренный. Следовательно, КМ –высота треугольника АКС(по св-ву), а значит, ВМ высота и треугольника АВС.

C
B
A
K
М
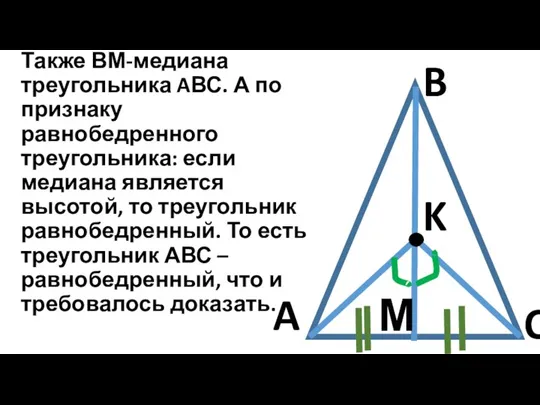
Также ВМ-медиана треугольника AВС. А по признаку равнобедренного треугольника: если медиана является высотой, то треугольник равнобедренный. То есть треугольник АВС –равнобедренный, что и требовалось доказать.