- Главная
- Математика
- Задачи на движение

Содержание
- 2. Движение является объектом рассмотрения в самых разнообразных задачах, в том числе и в задачах на части.
- 4. Задача 1. Два пешехода одновременно вышли навстречу друг другу из двух пунктов, расстояние между которыми 18
- 5. Задача 2. Два автомобиля выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 600
- 6. Есть и другие арифметические способы решения данной задачи, вот два из них. Допустим такой вид вспомогательной
- 8. Задача 3. Из двух пунктов, удаленных друг от друга на 30 км, выехали одновременно в одном
- 9. Задача 4. Всадник выезжает из пункта А и едет со скоростью 12 км/ч; в это же
- 11. Задача 6. Два поезда отошли одновременно от одной станции в противоположных направлениях. Их скорости 60 км/ч
- 12. Задача 7. От станции А отправился поезд со скоростью 60 км/ч. Через 2 ч с этой
- 14. Задача 8. Расстояние 360 км катер проходит за 15 ч, если двигается против течения реки, и
- 16. Скачать презентацию
Слайд 2Движение является объектом рассмотрения в самых разнообразных задачах, в том числе и
Движение является объектом рассмотрения в самых разнообразных задачах, в том числе и

S = V∙t, где S – пройденный путь; V – скорость движения; t – время движения, причем движение рассматривается равномерное прямолинейное.
Слайд 4Задача 1. Два пешехода одновременно вышли навстречу друг другу из двух пунктов,
Задача 1. Два пешехода одновременно вышли навстречу друг другу из двух пунктов,

Для решения такой задачи можно пользоваться любыми вспомогательными моделями – схематический чертеж или таблица.
Поиск плана решения удобно вести, рассуждая от данных к вопросу. Так как скорости пешеходов известны, можно найти их скорость сближения. Зная скорость сближения пешеходов и все расстояние, которое им надо пройти, можно найти время, через которое пешеходы встретятся.
5 + 4 = 9 (км/ч) – скорость сближения.
18 : 9 = 2 (ч)
Ответ: через 2 ч пешеходы встретились.
Слайд 5Задача 2. Два автомобиля выехали одновременно навстречу друг другу из двух пунктов,
Задача 2. Два автомобиля выехали одновременно навстречу друг другу из двух пунктов,

Поиск плана решения задачи будем вести, рассуждая от данных к вопросу. Так как известно все расстояние и время встречи, можно найти скорость сближения автомобилей. Затем, зная, что скорость одного на 16 км/ч больше скорости другого, можно найти скорости автомобилей.
600 : 5 = 120 (км/ч) – скорость сближения автомобилей.
120 – 16 = 104 (км/ч) – скорость сближения, если бы скорости автомобилей были одинаковыми и равными скорости первого.
104 : 2 = 52 (км/ч) – скорость первого автомобиля.
52 + 16 = 68 (км/ч) – скорость второго автомобиля.
Ответ: 52 км/ч и 68 км/ч
Слайд 6Есть и другие арифметические способы решения данной задачи, вот два из них.
Допустим
Есть и другие арифметические способы решения данной задачи, вот два из них.
Допустим

Слайд 8Задача 3. Из двух пунктов, удаленных друг от друга на 30 км,
Задача 3. Из двух пунктов, удаленных друг от друга на 30 км,

Сравнение скоростей мотоциклистов показывает, что в течение часа первый мотоциклист приближается ко второму на 10 км. Расстояние, которое ему надо пройти до встречи со вторым, на 30 км больше, чем расстояние, которое за такое же время проедет второй мотоциклист. Поэтому первому потребуется столько времени, сколько раз 10 км укладывается в 30 км.
50 – 40 = 10 (км/ч) – скорость сближения мотоциклистов.
30 : 10 = 3 (ч)
Ответ: через 3 часа второй мотоциклист догонит первого
Слайд 9Задача 4. Всадник выезжает из пункта А и едет со скоростью 12
Задача 4. Всадник выезжает из пункта А и едет со скоростью 12

Чтобы ответить на вопрос задачи, надо найти время, которое будет находиться в пути пешеход или всадник, - время их движения до встречи одинаковое.
12 – 4 = 8 (км/ч) – скорость сближения всадника и пешехода
24 : 8 = 3 (ч) – время, через которое всадник догонит пешехода
4 ∙ 3 = 12 (км)
Ответ: 12 км расстояние от пункта В , на котором всадник догонит пешехода.
Слайд 11Задача 6. Два поезда отошли одновременно от одной станции в противоположных направлениях.
Задача 6. Два поезда отошли одновременно от одной станции в противоположных направлениях.

60 ∙ 3 = 180 (км) – расстояние, пройденное первым поездом
70 ∙ 3 = 210 (км) – расстояние, пройденное вторым поездом
180 + 210 = 390 (км)
Ответ: 390 км расстояние между поездами через 3 часа.
Можно решить эту задачу другим способом, воспользовавшись понятием скорости удаления:
60 + 70 = 130 (км/ч) – скорость удаления поездов
130 ∙ 3 = 390 (км)
Ответ: 390 км расстояние между поездами через 3 часа.
Слайд 12Задача 7. От станции А отправился поезд со скоростью 60 км/ч. Через
Задача 7. От станции А отправился поезд со скоростью 60 км/ч. Через

Эта задача отличается от задачи 6 тем, что движение поездов начинается в разное время.
Слайд 14Задача 8. Расстояние 360 км катер проходит за 15 ч, если двигается
Задача 8. Расстояние 360 км катер проходит за 15 ч, если двигается

В данном случае удобно все данные, неизвестные и искомое, записать в таблицу:
360 : 12 = 30 (км/ч) – скорость катера по течению реки
360 : 15 = 24 (км/ч) – скорость катера против течения реки
24 + 30 = 54 (км/ч) – удвоенная собственная скорость катера
54 : 2 = 27 (км/ч) – собственная скорость катера
135 : 27 = 5 (ч)
Ответ: 5 ч потребуется катеру, чтобы проплыть 135 км оп озеру




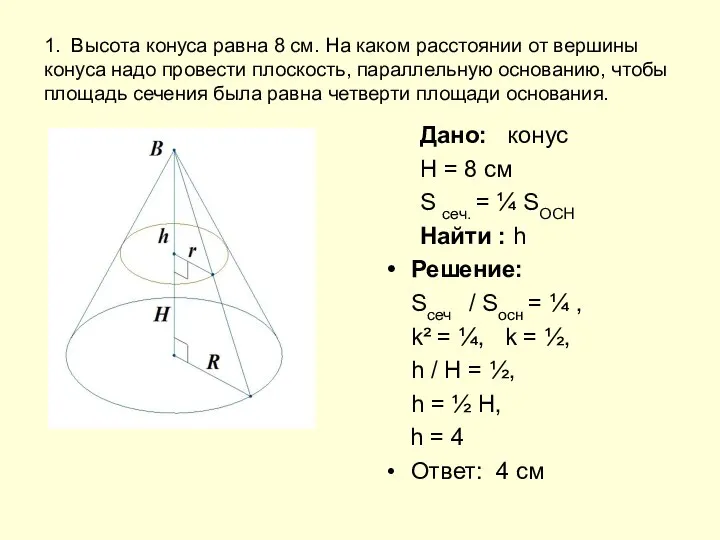 Объём конуса
Объём конуса Смежные и вертикальные углы
Смежные и вертикальные углы Человек и число
Человек и число Статистика. Занятие 3
Статистика. Занятие 3 Решение уравнений (2 класс)
Решение уравнений (2 класс) Тренажер-раскраска Заинька. Математика 1 класс. Сложение и вычитание в пределах 5
Тренажер-раскраска Заинька. Математика 1 класс. Сложение и вычитание в пределах 5 Формулы тригонометрии
Формулы тригонометрии Презентация на тему Тест по теме "Площади"
Презентация на тему Тест по теме "Площади"  Начала теории вероятностей
Начала теории вероятностей Первообразная и интеграл
Первообразная и интеграл Функция регрессии
Функция регрессии Подготовка к ВПР
Подготовка к ВПР С 6 класса
С 6 класса Решение уравнений. Задание №21 ОГЭ
Решение уравнений. Задание №21 ОГЭ Тригонометрические функции, их свойства и графики
Тригонометрические функции, их свойства и графики Игра путешествие В гостях у Незнайки
Игра путешествие В гостях у Незнайки Уравнение прямой
Уравнение прямой Аналитическая геометрия. Уравнения прямой
Аналитическая геометрия. Уравнения прямой Математична Legoманiя
Математична Legoманiя Математическая игра
Математическая игра Разделение переменных в уравнении Лапласа в сферических координатах. Сферические и шаровые функции Лапласа
Разделение переменных в уравнении Лапласа в сферических координатах. Сферические и шаровые функции Лапласа Дидактическая игра Гравити Фолз по математике для учеников 6 класса направленная на итоговое повторение
Дидактическая игра Гравити Фолз по математике для учеников 6 класса направленная на итоговое повторение Площадь параллелограмма
Площадь параллелограмма Делители числа
Делители числа Показательные неравенства, их типы и методы решения
Показательные неравенства, их типы и методы решения Факториал. Теорема
Факториал. Теорема График функции
График функции Сложение десятичных дробей
Сложение десятичных дробей