«воображаемый»)
"Комплексными числами и функциями комплексного переменного математики пользовались в своих исследованиях уже в XVIII в. Особенно велики заслуги крупнейшего математика XVIII в. Леонарда Эйлера (1707—1783), который по праву считается одним из творцов теории функций комплексного переменного. В замечательных работах Эйлера детально изучены элементарные функции комплексного переменного.
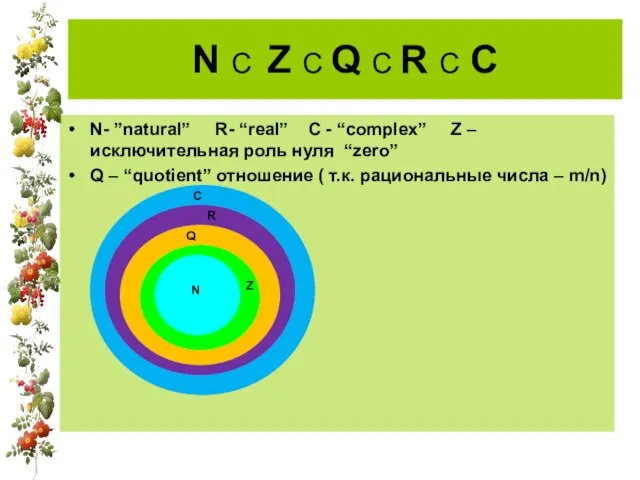
После Эйлера открытые им результаты и методы развивались, совершенствовались и систематизировались, и в первой половине XIX в. теория функций комплексного переменного оформилась как важнейшая отрасль математического анализа. "Первое упоминание о «мнимых» числах как о корнях квадратных и» отрицательных чисел относится еще к XVI в. (Дж. К а р д а н о, 1545). До середины XVIII в. комплексные числа появляются лишь эпизодически в трудах отдельных математиков (И. Ньютон, Н. Бернулли, А. Клеро). Первое изложение теории комплексных чисел на русском языке принадлежит Л. Эйлеру («Алгебра», Петербург, 1763, позднее книга была переведена на иностранные языки и многократно переиздавалась): символ «i» также введен Л. Эйлером. Геометрическая интерпретация комплексных чисел относится к концу XVIII в. (датчанин Каспар Вессель, 1799 г.)."




 Сложение и вычитание векторов
Сложение и вычитание векторов Призмы. Виды призм
Призмы. Виды призм Численное интегрирование
Численное интегрирование Незнайка на планете Математика
Незнайка на планете Математика Решение задач
Решение задач Решение экономических задач
Решение экономических задач Презентация на тему Операции. Обратные операции
Презентация на тему Операции. Обратные операции  Меры длины и веса. Задания
Меры длины и веса. Задания Геометричний метод розв’язування задач лінійного програмування. Методи оптимізації. Лекція №2
Геометричний метод розв’язування задач лінійного програмування. Методи оптимізації. Лекція №2 Тренажер. Смешарики. Сложение в пределах 20
Тренажер. Смешарики. Сложение в пределах 20 Определенный интеграл
Определенный интеграл Сравнение трехзначных чисел
Сравнение трехзначных чисел Статистическая сводка и группировка
Статистическая сводка и группировка Презентация на тему Делимость чисел
Презентация на тему Делимость чисел  Прямоугольный параллелепипед
Прямоугольный параллелепипед Многогранники, символы красоты и совершенства
Многогранники, символы красоты и совершенства Математика в профессиях
Математика в профессиях Математика и режим дня
Математика и режим дня Случаи сложения 470 +80 и вычитания 560-90
Случаи сложения 470 +80 и вычитания 560-90 Умножение десятичной дроби на десятичную дробь
Умножение десятичной дроби на десятичную дробь Видовые числа и коэффициенты формы стволов деревьев
Видовые числа и коэффициенты формы стволов деревьев Площадь многоугольника. Свойства площадей
Площадь многоугольника. Свойства площадей Преимущества урока с ИКТ
Преимущества урока с ИКТ Равенство. Неравенство
Равенство. Неравенство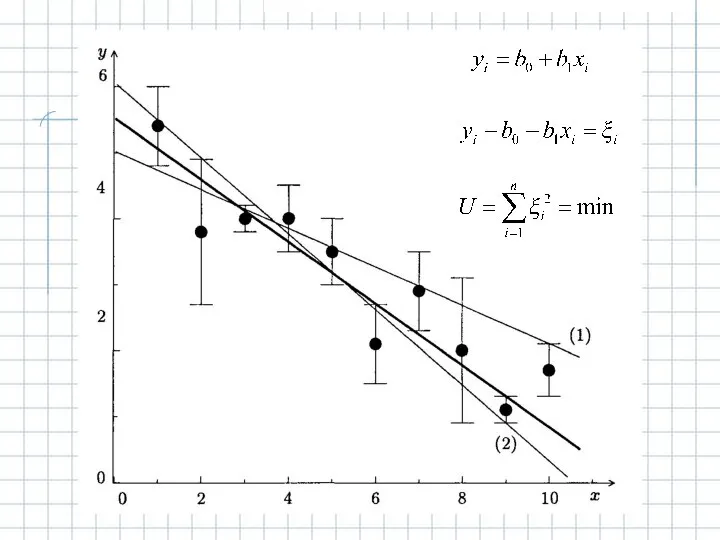 Расчет коэффициентов регрессии (МНК)
Расчет коэффициентов регрессии (МНК) Свойства медианы треугольника
Свойства медианы треугольника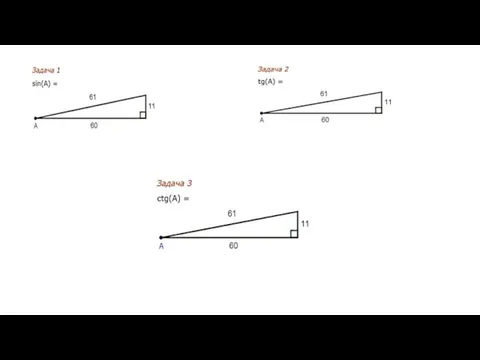 Решение примеров
Решение примеров Свойство описанного четырехугольника
Свойство описанного четырехугольника