Содержание
- 2. Интегрирование Операция нахождения интеграла называется интегрированием. Операции интегрирования и дифференцирования обратны друг другу в следующем смысле:
- 3. Первообразная Первообразной функции f(x) называется такая функция F(x), производная которой равна f(x): F΄(x) = f(x)
- 4. Неопределённый интеграл Запись вида F (x) = ∫ f(x) dx, где f(x) – функция действительного аргумента,
- 5. Значение неопределённого интеграла Производные двух функций, отличающихся на константу, совпадают, поэтому в выражение для неопределенного интеграла
- 6. Геометрический смысл неопределённого интеграла Геометрически неопределенный интеграл представляет собой семейство интегральных кривых, полученных параллельным переносом графика
- 7. Определённый интеграл Об определенном интеграле есть смысл говорить на отрезке интегрирования [a, b]
- 8. Значение определённого интеграла Значение определенного интеграла вычисляется по формуле Ньютона-Лейбница
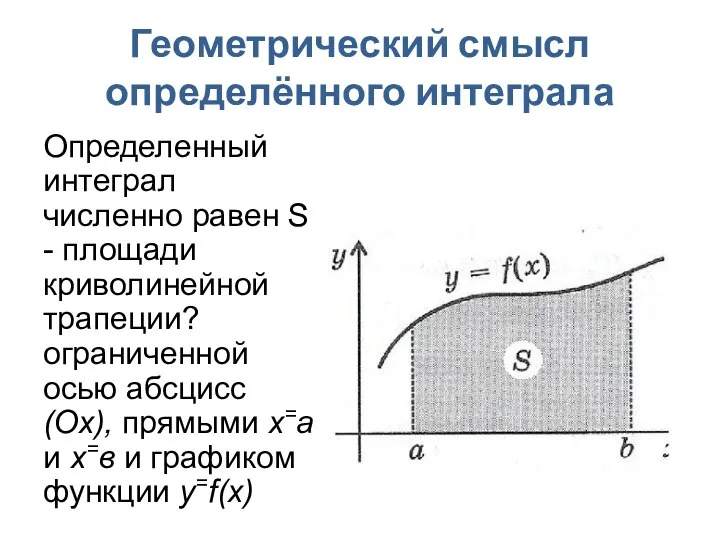
- 9. Геометрический смысл определённого интеграла Определенный интеграл численно равен S - площади криволинейной трапеции? ограниченной осью абсцисс
- 10. Случаи применения численных методов для интегрирования Численные методы интегрирования применяются, когда невозможно или затруднительно воспользоваться Ньютона-Лейбница,
- 11. Методы в численном интегрировании В случае численного интегрирования прибегают к приближенному нахождению интеграла, для чего подынтегральную
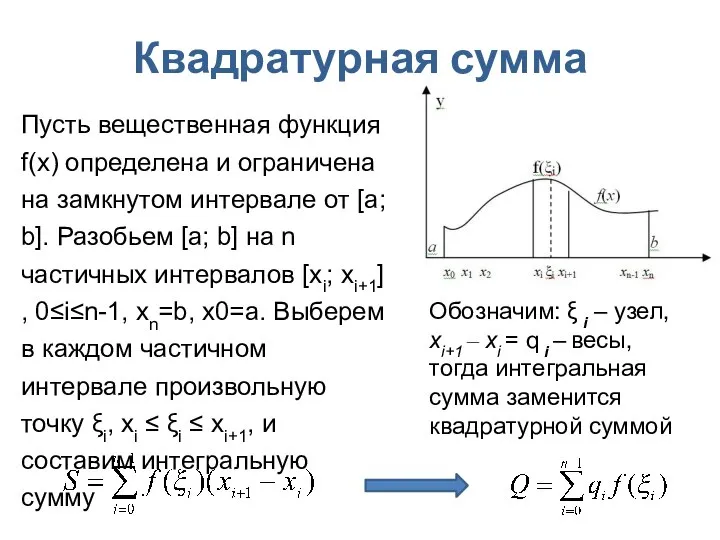
- 12. Квадратурная сумма Пусть вещественная функция f(x) определена и ограничена на замкнутом интервале от [a; b]. Разобьем
- 13. Общий вид квадратурной формулы R называется погрешностью, или остаточным членом квадратурной формулы. Чтобы получить конкретную квадратурную
- 14. Формула прямоугольников. Идея Разобьем [a, b] на n равных отрезков с шагом h=(b-a)/2 точками x0=a x1=a+h
- 15. Формула прямоугольников. Геометрический смысл На каждом отрезке [xi; xi+1] графически прямая P0(xi) = f(xi) = yi
- 16. Формула прямоугольников. Вид для вычислений
- 17. Формула трапеции. Идея Разобьем [a, b] на n равных отрезков с шагом h=(b-a)/2 точками xk=x1+kh, k=1,…,n
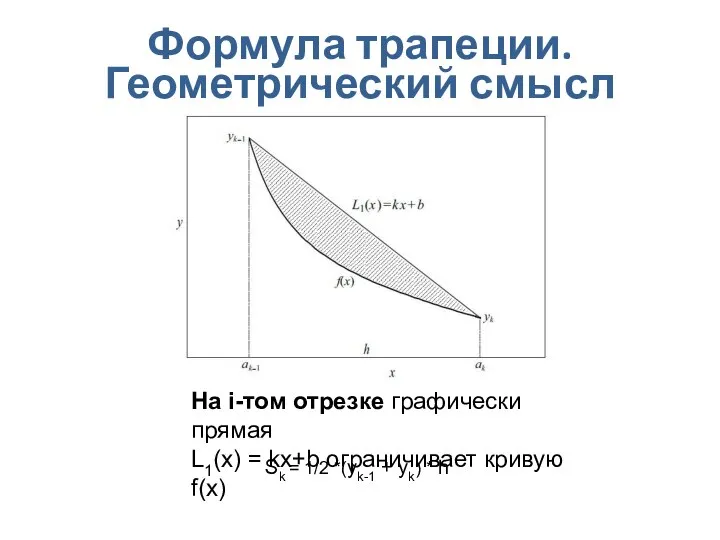
- 18. Формула трапеции. Геометрический смысл На i-том отрезке графически прямая L1(x) = kx+b ограничивает кривую f(x) Sk
- 19. Формула трапеции. Вид для вычислений
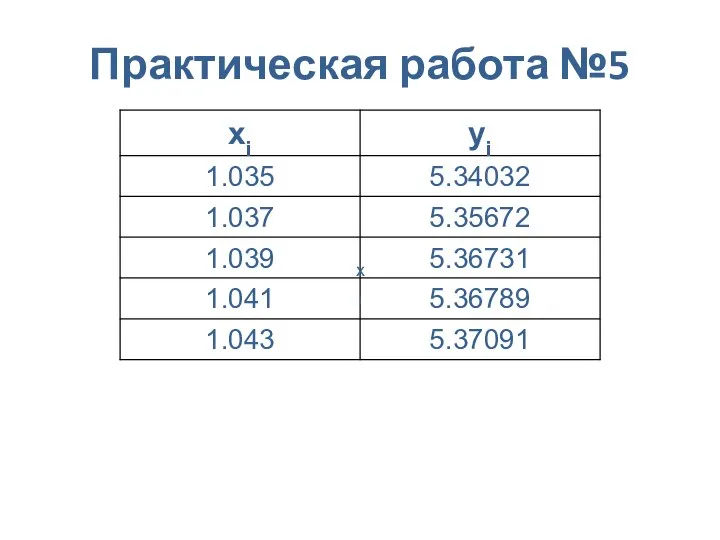
- 20. Практическая работа №5 Задание Вычислить приближенно на отрезке [x0, x4] интеграл функции, заданной таблично, по формуле
- 21. Практическая работа №5 Пример xi
- 22. Вычисления по формуле прямоугольников. h = | 1,035 – 1,037| = 0,002 I = 0,002 *
- 24. Скачать презентацию





![Определённый интеграл Об определенном интеграле есть смысл говорить на отрезке интегрирования [a, b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/978622/slide-6.jpg)




![Формула прямоугольников. Идея Разобьем [a, b] на n равных отрезков с шагом](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/978622/slide-13.jpg)
![Формула прямоугольников. Геометрический смысл На каждом отрезке [xi; xi+1] графически прямая P0(xi)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/978622/slide-14.jpg)

![Формула трапеции. Идея Разобьем [a, b] на n равных отрезков с шагом](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/978622/slide-16.jpg)

![Практическая работа №5 Задание Вычислить приближенно на отрезке [x0, x4] интеграл функции,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/978622/slide-19.jpg)

 Свойства логарифмов
Свойства логарифмов Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Координатная плоскость
Координатная плоскость Показательные и логарифмические уравнения, системы, неравенства
Показательные и логарифмические уравнения, системы, неравенства Числа 6 и 7. Письмо цифры 7 (1 класс)
Числа 6 и 7. Письмо цифры 7 (1 класс) Справочник по геометрии
Справочник по геометрии Презентация на тему Высказывания со словами: есть, существует, некоторые
Презентация на тему Высказывания со словами: есть, существует, некоторые  Подстановки, оптимизация и решение дифференциальных уравнений (задача Коши)
Подстановки, оптимизация и решение дифференциальных уравнений (задача Коши) Решение задач по теме: Объем цилиндра 11 класс
Решение задач по теме: Объем цилиндра 11 класс Распределительное свойства умножения
Распределительное свойства умножения Общее решение неполного квадратного уравнения. 8 класс
Общее решение неполного квадратного уравнения. 8 класс Задания по геометрии
Задания по геометрии Составление алгоритма
Составление алгоритма Конус
Конус Логарифмические уравнения
Логарифмические уравнения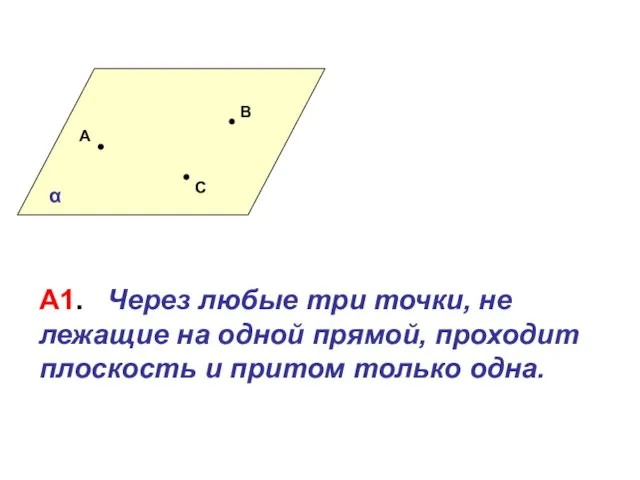 Плоскости
Плоскости Комплексные числа и действия над ними
Комплексные числа и действия над ними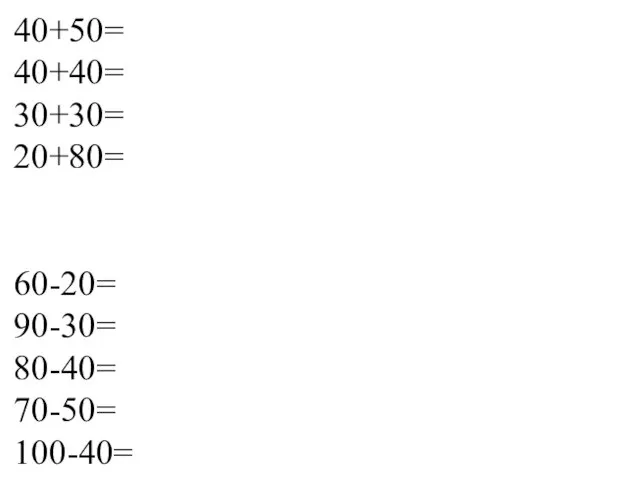 Найди значение выражений
Найди значение выражений Размерность. Единицы измерения
Размерность. Единицы измерения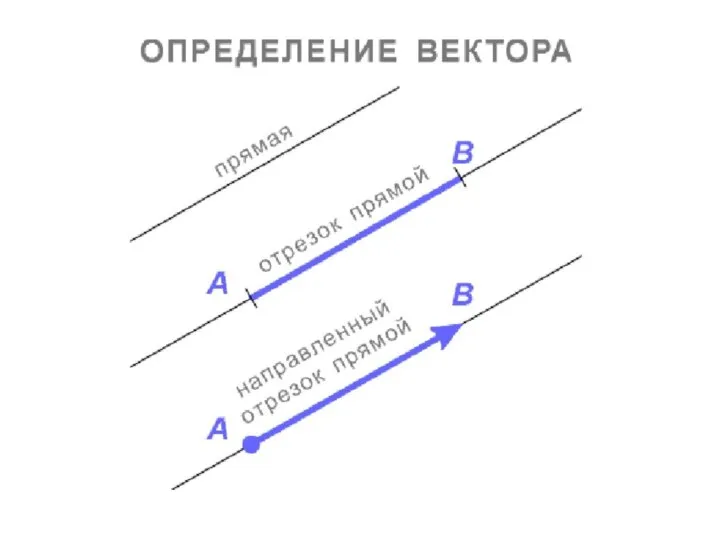 Определение вектора
Определение вектора Закрепление изученного. Решение задач
Закрепление изученного. Решение задач Понятие цилиндра
Понятие цилиндра Коэффициент корреляции
Коэффициент корреляции Презентация на тему Деление многозначного числа на однозначное
Презентация на тему Деление многозначного числа на однозначное  Формула полной вероятности и формула Байеса. Формула Бернулли. Лекция 3
Формула полной вероятности и формула Байеса. Формула Бернулли. Лекция 3 Умножение на 2. Проведите динозаврика по лабиринту (2)
Умножение на 2. Проведите динозаврика по лабиринту (2) Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Системы степенных неравенств
Системы степенных неравенств