- Главная
- Математика
- Статистическая сводка и группировка

Содержание
- 2. Литература Неганова Л.М. Статистика.
- 3. 3.1. Задачи сводки и ее содержание Научно организованная обработка материалов статистического наблюдения по заранее разработанной программе
- 4. 3.1. Задачи сводки и ее содержание Сводка материалов наблюдения - комплекс последовательных действий по обобщению конкретных
- 5. 3.1. Задачи сводки и ее содержание Задача сводки - дать характеристику объекту исследования с помощью систем
- 6. 3.1. Задачи сводки и ее содержание Перечисленные этапы сводки еще до начала ее проведения отражаются в
- 7. 3.2. Основные задачи и виды группировок Предмет статистических исследований - массовые явления и процессы общественной жизни
- 8. 3.2. Основные задачи и виды группировок Статистические группировки - первый этап статистической сводки, позволяющий выделить из
- 9. 3.2. Основные задачи и виды группировок Основополагающим принципом применения метода группировок является всесторонний, глубокий анализ сущности
- 10. 3.2. Основные задачи и виды группировок На основе применения метода группировок определяются группы по принципу подобия
- 11. 3.2. Основные задачи и виды группировок Основные задачи, решаемые с помощью группировок, в статистике : •
- 12. 3.2. Основные задачи и виды группировок Пример типологической группировки - группировка по виду участвующих субъектов инновационной
- 13. 3.2. Основные задачи и виды группировок Важное значение имеет Изучение структуры общественных явлений - изучение различий
- 14. 3.2. Основные задачи и виды группировок Например, группировка в табл. 3.2 показывает, что в период с
- 15. 3.2. Основные задачи и виды группировок В основу структурных группировок могут быть положены атрибутивный или количественный
- 16. 3.2. Основные задачи и виды группировок В табл. 3.3 приведена структурная группировка по количественному признаку. В
- 17. 3.2. Основные задачи и виды группировок Если применяются равные интервалы, то расчет их величины производится по
- 18. 3.2. Основные задачи и виды группировок Одна из целей статистического наблюдения - выявление связей и зависимостей
- 19. 3.2. Основные задачи и виды группировок Важная проблема аналитических группировок - правильный выбор числа групп и
- 20. 3.2. Основные задачи и виды группировок Непосредственная группировка данных статистического наблюдения -это первичная группировка. Вторичная группировка
- 21. 3.2. Основные задачи и виды группировок В научно обоснованной группировке общественных явлений необходимо учитывать взаимозависимость явлений
- 22. 3.2. Основные задачи и виды группировок Самая простая группировка - ряд распределения. Ряд распределения - ряды
- 23. 3.2. Основные задачи и виды группировок Вариационные ряды - ряды распределения, построенные по количественному признаку. Числовые
- 24. 3.2. Основные задачи и виды группировок
- 25. 3.2. Основные задачи и виды группировок При построении интервального вариационного ряда необходимо выбрать оптимальное число групп
- 26. 3.2. Основные задачи и виды группировок Если полученная группировка не удовлетворяет требованиям анализа, то можно произвести
- 27. 3.3. Статистические таблицы После того как данные статистического наблюдения собраны и даже сгруппированы, их трудно воспринимать
- 28. 3.3. Статистические таблицы Подлежащее таблицы представляет ту статистическую совокупность, о которой идет речь в таблице, т.
- 29. 3.3. Статистические таблицы В статистической практике и исследовательских работах используются таблицы различной сложности. Это зависит от
- 30. 3.3. Статистические таблицы Групповые таблицы в отличие от простых содержат в подлежащем не простой перечень единиц
- 31. 3.3. Статистические таблицы Наряду с перечисленными выше таблицами в статистической практике применяют таблицы сопряженности, или таблицы
- 32. 3.3. Статистические таблицы Из всех видов статистических таблиц наиболее широкое применение имеют простые таблицы, реже применяются
- 33. 3.3. Статистические таблицы Основные правила построения статистических таблиц: • таблица должна быть компактной и отражать только
- 34. 3.3. Статистические таблицы Основные правила построения статистических таблиц: • для удобства чтения и работы числа в
- 35. 3.3. Статистические таблицы В случае необходимости дополнительной информации статистические таблицы сопровождаются сносками и примечаниями, в которых
- 36. 3.4. Графические представления статистической информации Полученные в результате сводки или статистического анализа в целом числовые показатели
- 37. 3.4. Графические представления статистической информации Каждый график состоит из графического образа и вспомогательных элементов. Графический образ
- 38. 3.4. Графические представления статистической информации Оси координат с нанесенными на них шкалами и числовые сетки необходимы
- 39. 3.4. Графические представления статистической информации По содержанию, или назначению, можно выделить: графики сравнения в пространстве; графики
- 40. 3.4. Графические представления статистической информации По способу построения графики можно разделить на диаграммы и статистические карты.
- 41. 3.4. Графические представления статистической информации В зависимости от круга решаемых задач выделяются диаграммы сравнения, структурные диаграммы
- 42. 3.4. Графические представления статистической информации Статистические карты представляют собой вид графических изображений статистических данных на схематичной
- 46. Скачать презентацию
Слайд 33.1. Задачи сводки и ее содержание
Научно организованная обработка материалов статистического наблюдения по
3.1. Задачи сводки и ее содержание
Научно организованная обработка материалов статистического наблюдения по

Собранный в процессе статистического наблюдения материал представляет собой разрозненные первичные сведения об отдельных единицах изучаемого явления.
В таком виде материал еще не характеризует явление в целом: не дает представления ни о величине (численности) явления, ни о его составе, ни о размере характерных признаков, ни о существе связей этого явления с другими явлениями и т. д.
Возникает необходимость в специальной обработке статистических данных - сводке материалов наблюдения.
Слайд 43.1. Задачи сводки и ее содержание
Сводка материалов наблюдения - комплекс последовательных действий
3.1. Задачи сводки и ее содержание
Сводка материалов наблюдения - комплекс последовательных действий

Статистическая сводка (простая сводка) в узком смысле слова представляет собой операцию по подсчету общих итоговых (суммарных) данных по совокупности единиц наблюдения.
Статистическая сводка (сложная сводка) в широком смысле слова включает в себя также группировку данных наблюдения, подсчет общих и групповых итогов, получение системы взаимосвязанных показателей, представление результатов группировки и сводки в виде статистических таблиц.
Правильная, научно организованная сводка, опираясь на предварительный глубокий теоретический анализ, позволяет получить все статистические итоги, отражающие важнейшие, характерные черты объекта исследования, измерить влияние различных факторов на результат и учесть все это в практической работе при составлении текущих и перспективных планов.
Слайд 53.1. Задачи сводки и ее содержание
Задача сводки - дать характеристику объекту исследования
3.1. Задачи сводки и ее содержание
Задача сводки - дать характеристику объекту исследования

Эта задача решается на трех этапах:
• определение групп и подгрупп;
• определение системы показателей;
• определение видов таблиц.
На первом этапе осуществляется систематизация, группировка материалов, собранных при наблюдении.
На втором этапе уточняется предусмотренная планом система показателей, с помощью которых количественно характеризуются свойства и особенности изучаемого предмета.
На третьем этапе исчисляются сами показатели, и обобщенные данные для наглядности и удобства представляются в таблицах, статистических рядах, графиках, диаграммах.
Слайд 63.1. Задачи сводки и ее содержание
Перечисленные этапы сводки еще до начала ее
3.1. Задачи сводки и ее содержание
Перечисленные этапы сводки еще до начала ее

Программа статистической сводки содержит перечень групп, на которые целесообразно разделить совокупность, их границы в соответствии с группировочными признаками; систему показателей, характеризующих совокупность, и методику их расчета; систему макетов разработочных таблиц, в которых будут представлены итоги расчетов.
План проведения сводки - предусматривает ее организацию. План проведения сводки должен содержать указания о последовательности и сроках выполнения ее отдельных частей, об ответственных за ее выполнение, порядке изложения результатов, а также предусматривать координацию работы всех организаций, задействованных в ее проведении.
Слайд 73.2. Основные задачи и виды группировок
Предмет статистических исследований - массовые явления и
3.2. Основные задачи и виды группировок
Предмет статистических исследований - массовые явления и

Обобщить статистические данные, раскрыть наиболее существенные особенности, формы развития массового явления в целом и отдельных его составляющих невозможно без определенных научных принципов обработки данных.
Без преодоления индивидуального многообразия объектов статистического наблюдения общие закономерности развития явления или процесса в целом теряются в деталях и мелочах, отличающих каждый объект один от другого, а предельное обобщение влечет за собой извращенное представление о действительности.
Для разделения совокупности единиц на однотипные группы статистика использует метод группировок.
Слайд 83.2. Основные задачи и виды группировок
Статистические группировки - первый этап статистической сводки,
3.2. Основные задачи и виды группировок
Статистические группировки - первый этап статистической сводки,

Важно понимать, что группировка - это не субъективный технический прием разделения совокупности на части, а научно обоснованный процесс разделения множества единиц совокупности по определенному признаку.
Слайд 93.2. Основные задачи и виды группировок
Основополагающим принципом применения метода группировок является всесторонний,
3.2. Основные задачи и виды группировок
Основополагающим принципом применения метода группировок является всесторонний,

Любая общая совокупность является комплексом частных совокупностей, каждая из которых объединяет явления особого типа, однокачественные в определенном отношении. Каждый тип (группа) имеет специфическую систему признаков с соответствующим уровнем их количественных значений.
Установить, к какому типу, в какую частную совокупность нужно отнести группируемые единицы общей совокупности, возможно на основе правильного, четкого определения существенных признаков, по которым должна проводиться группировка. Это второе важное требование научно обоснованной группировки.
Третье требование группировки основано на объективном, обоснованном установлении границ групп при условии, что образованные группы должны объединять однородные элементы совокупности, а сами группы (одна по отношению к другой) должны существенно различаться. В противном случае группировка теряет смысл.
Слайд 103.2. Основные задачи и виды группировок
На основе применения метода группировок определяются группы
3.2. Основные задачи и виды группировок
На основе применения метода группировок определяются группы

Подобие - это однородность единиц в определенных пределах (группах);
Различие - это их существенное расхождение по группам.
Группировка - разделение общей совокупности единиц по одному или нескольким существенным признакам на однородные группы, различающиеся между собой в качественном и количественном отношении и позволяющие выделить социально-экономические типы, изучить структуру совокупности или проанализировать связи между отдельными признаками.
Разнообразие общественных явлений и целей их изучения делает возможным применение большого количества статистических группировок явлений и решение на этой основе самых различных конкретных задач.
Слайд 113.2. Основные задачи и виды группировок
Основные задачи, решаемые с помощью группировок, в
3.2. Основные задачи и виды группировок
Основные задачи, решаемые с помощью группировок, в

• выделение в совокупности изучаемых явлений их социально-экономических типов;
• изучение структуры общественных явлений;
• выявление связей и зависимостей между общественными явлениями.
Все группировки, связанные с выделением в совокупности изучаемых явлений их социально-экономических типов, занимают в статистике центральное место. Эта задача имеет отношение к наиболее существенным, решающим сторонам общественной жизни, например группировка населения по социальному статусу, полу, возрасту, уровню образования, группировка предприятий и организаций по формам собственности, отраслевой принадлежности.
Построение подобных группировок за продолжительные периоды позволяет проследить процесс развития социально-экономических отношений. Задача расчленения совокупности общественных явлений по их социально-экономическим типам решается с помощью построения типологических группировок.
Типологическая группировка - это разделение качественно разнородной исследуемой совокупности на однородные группы единиц в соответствии с социально-экономическими типами.
Слайд 123.2. Основные задачи и виды группировок
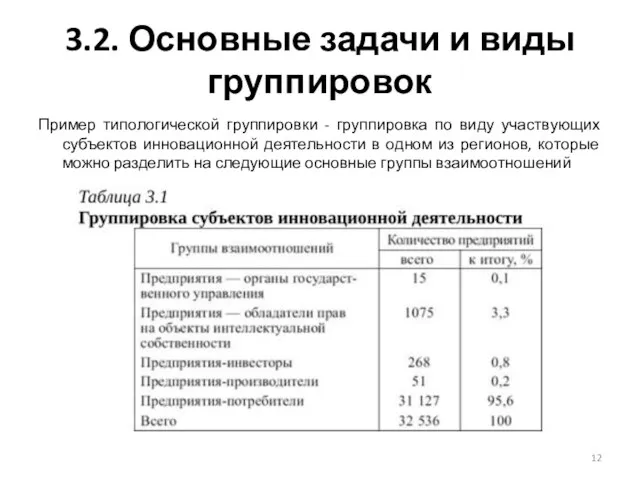
Пример типологической группировки - группировка по виду
3.2. Основные задачи и виды группировок
Пример типологической группировки - группировка по виду
Слайд 133.2. Основные задачи и виды группировок
Важное значение имеет
Изучение структуры общественных явлений
3.2. Основные задачи и виды группировок
Важное значение имеет
Изучение структуры общественных явлений

Структурная группировка - группировка, в которой происходит разделение однородной совокупности на группы, характеризующие ее структуру по какому-либо варьирующему признаку.
К структурным группировкам относятся группировка населения по полу, возрасту, уровню образования, группировка предприятий по численности работников, уровню заработной платы, объему работ и т. д. В изменении структуры общественных явлений отражаются важнейшие закономерности их развития.
Применение структурных группировок позволяет не только раскрыть структуру совокупности, но и проанализировать изучаемые процессы, их интенсивность, изменение в пространстве, а взятые за ряд периодов времени структурные группировки раскрывают закономерности изменений состава совокупности во времени.
Слайд 143.2. Основные задачи и виды группировок
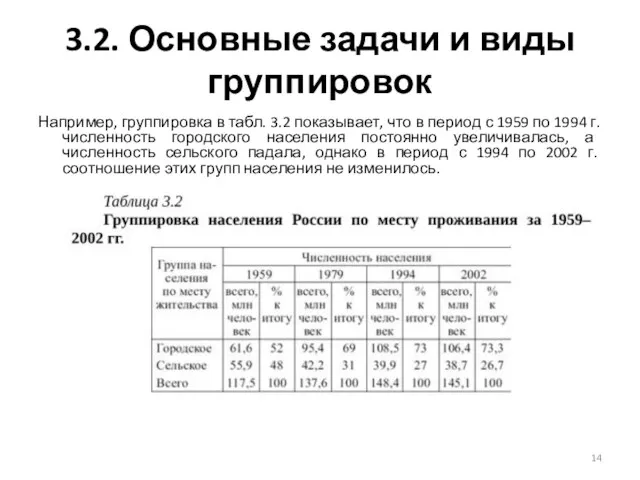
Например, группировка в табл. 3.2 показывает, что
3.2. Основные задачи и виды группировок
Например, группировка в табл. 3.2 показывает, что
Слайд 153.2. Основные задачи и виды группировок
В основу структурных группировок могут быть положены
3.2. Основные задачи и виды группировок
В основу структурных группировок могут быть положены

Их выбор определяется задачами конкретного исследования и сущностью изучаемой совокупности.
Группировка, приведенная в табл. 3.2, построена по атрибутивному признаку.
При структурной группировке по количественному признаку возникает необходимость определения числа групп и их границ.
Этот вопрос решается в соответствии с задачами исследования. Один и тот же статистический материал может быть разбит на группы различным образом в зависимости от целей и задач исследования. Главное, чтобы в процессе группировки были ярко отражены особенности изучаемого явления и созданы предпосылки для конкретных выводов и рекомендаций.
Слайд 163.2. Основные задачи и виды группировок
В табл. 3.3 приведена структурная группировка по
3.2. Основные задачи и виды группировок
В табл. 3.3 приведена структурная группировка по

В данной таблице интервалы групп равны по своей величине.
Слайд 173.2. Основные задачи и виды группировок
Если применяются равные интервалы, то расчет их
3.2. Основные задачи и виды группировок
Если применяются равные интервалы, то расчет их

(3.1)
где h - величина интервала, xmax и xmin - максимальные и минимальные значения признаков совокупности, к - число групп.
Следует отметить, что технически удобнее иметь дело с равными интервалами, но это далеко не всегда представляется возможным из-за свойств изучаемых явлений и признаков. В экономике чаще приходится применять неравные, прогрессивно увеличивающиеся интервалы, что обусловлено самой природой экономических явлений.
Применение неравных интервалов объясняется главным образом тем, что абсолютное изменение группировочного признака на одну и ту же величину имеет далеко не одинаковое значение для групп с большим и малым значением признака. Например, между двумя предприятиями с численностью рабочих до 300 человек разница в 100 человек более существенна, чем для предприятий с численностью свыше 10 000 человек.
Интервалы групп могут быть замкнутыми, когда указаны нижняя и верхняя границы, и открытыми, когда указана лишь одна из границ групп.
Открытые интервалы применяются только для крайних групп. При группировке с неравными интервалами желательно образование групп с замкнутыми интервалами. Это способствует точности статистических вычислений.
Слайд 183.2. Основные задачи и виды группировок
Одна из целей статистического наблюдения - выявление
3.2. Основные задачи и виды группировок
Одна из целей статистического наблюдения - выявление

Важной задачей статистического анализа, проводимого на основе типологической группировки, т. е. в пределах однокачественных совокупностей, является задача изучения и измерения связи между отдельными признаками. Установить факт наличия такой связи позволяет аналитическая группировка.
Аналитическая группировка - распространенный прием статистического изучения связей, которые обнаруживаются при параллельном сопоставлении обобщенных значений признаков по группам.
Различают признаки зависимые, значения которых изменяются под влиянием других признаков, их обычно в статистике называют результативными, и факторные, оказывающие влияние на другие.
Обычно в основе аналитической группировки лежит признак-фактор, а по результативным признакам производится расчет групповых средних, по изменению величины которых определяют наличие связи между признаками.
Таким образом, аналитическими можно назвать такие группировки, которые позволяют установить и изучить связь между результативными и факторными признаками единиц однотипной совокупности.
Слайд 193.2. Основные задачи и виды группировок
Важная проблема аналитических группировок - правильный выбор
3.2. Основные задачи и виды группировок
Важная проблема аналитических группировок - правильный выбор

Поскольку анализ ведется в однокачественных совокупностях, теоретических оснований для дробления определенного типа нет, поэтому допустима разбивка совокупности на любое число групп, удовлетворяющее определенным требованиям и условиям конкретного анализа.
В процессе аналитических группировок следует соблюдать общие правила группировки, т. е. единицы в образованных группах должны быть существенно различны, количество единиц в группах должно быть достаточным для расчета надежных статистических характеристик.
Кроме того, групповые средние должны подчиняться определенной закономерности: последовательно увеличиваться или уменьшаться.
Слайд 203.2. Основные задачи и виды группировок
Непосредственная группировка данных статистического наблюдения -это первичная
3.2. Основные задачи и виды группировок
Непосредственная группировка данных статистического наблюдения -это первичная

Вторичная группировка - перегруппировка ранее сгруппированных данных.
Необходимость вторичной группировки возникает в двух случаях:
• ранее произведенная группировка не удовлетворяет целям исследования в отношении числа групп;
• для сравнения данных, относящихся к различным периодам времени или к различным территориям, если первичная группировка была произведена по разным группировочным признакам или по разным интервалам.
Существует два способа вторичной группировки:
• объединение мелких групп в более крупные;
• выделение определенной доли единиц совокупности.
Слайд 213.2. Основные задачи и виды группировок
В научно обоснованной группировке общественных явлений необходимо
3.2. Основные задачи и виды группировок
В научно обоснованной группировке общественных явлений необходимо

Если группировка - это распределение на однородные группы по какому-либо признаку или объединение отдельных единиц совокупности в группы, однородные по какому-либо признаку, то группировочный признак - это признак, по которому происходит объединение отдельных единиц совокупности в отдельные группы.
При выборе группировочного признака важным является не способ выражения признака, а его значение для изучаемого явления. С этой точки зрения для группировки следует брать существенные признаки, выражающие наиболее характерные черты изучаемого явления.
Слайд 223.2. Основные задачи и виды группировок
Самая простая группировка - ряд распределения.
Ряд
3.2. Основные задачи и виды группировок
Самая простая группировка - ряд распределения.
Ряд

Приведенный ряд распределения содержит три элемента: разновидность атрибутивного признака (мужчины, женщины); численность единиц в каждой группе, называемая частотами ряда распределения; численность групп, выраженная в долях (процентах) от общей численности единиц, называемая частостями. Сумма частостей равна 1, если они выражены в долях единицы, и равна 100 %, если они выражены в процентах.
Ряды, построенные по атрибутивному признаку, называют атрибутивными.
Слайд 233.2. Основные задачи и виды группировок
Вариационные ряды - ряды распределения, построенные по
3.2. Основные задачи и виды группировок
Вариационные ряды - ряды распределения, построенные по

Числовые значения количественного признака в вариационном ряду распределения называются вариантами и располагаются в определенной последовательности. Варианты могут выражаться числами положительными и отрицательными, абсолютными и относительными.
Вариационные ряды делятся на дискретные и интервальные.
Дискретные вариационные ряды характеризуют распределение единиц совокупности по дискретному (прерывному) признаку, т. е. принимающему целые значения. При построении ряда распределения с дискретной вариацией признака все варианты выписываются в порядке возрастания их величины, подсчитывается, сколько раз повторяется одна и та же величина варианта, т. е. частота, и записывается в одной строке с соответствующим значением варианта, например распределение семей по числу детей (табл. 3.5).
Частоты в дискретном вариационном ряду, как и в атрибутивном, могут быть заменены частостями.
В случае непрерывной вариации величина признака может принимать любые значения в определенном интервале, например распределение работников фирмы по уровню дохода (табл. 3.6).
Слайд 243.2. Основные задачи и виды группировок
3.2. Основные задачи и виды группировок

Слайд 253.2. Основные задачи и виды группировок
При построении интервального вариационного ряда необходимо выбрать
3.2. Основные задачи и виды группировок
При построении интервального вариационного ряда необходимо выбрать

где к - число групп; N - численность совокупности.
Например, необходимо построить вариационный ряд сельскохозяйственных предприятий по урожайности зерновых культур. Число сельскохозяйственных предприятий - 143. Как определить число групп?
Число групп может быть только целым числом, в данном случае - 8 или 9.
Пример. Минимальная урожайность составляет 30 ц/га, максимальная - 70 ц/га, а число намеченных групп - 10. Величину интервала можно рассчитать по формуле (3.1):
Слайд 263.2. Основные задачи и виды группировок
Если полученная группировка не удовлетворяет требованиям анализа,
3.2. Основные задачи и виды группировок
Если полученная группировка не удовлетворяет требованиям анализа,

Таким образом, группировки во всех случаях должны быть построены так, чтобы образованные в них группы как можно полнее отвечали действительности, были видны различия между группами и в одну группу не объединялись существенно различающиеся между собой явления.
Слайд 273.3. Статистические таблицы
После того как данные статистического наблюдения собраны и даже сгруппированы,
3.3. Статистические таблицы
После того как данные статистического наблюдения собраны и даже сгруппированы,

Статистическая таблица дает количественную характеристику статистической совокупности и представляет собой форму наглядного отображения полученных в результате статистической сводки и группировки числовых (цифровых) данных.
По внешнему виду таблица представляет собой комбинацию вертикальных и горизонтальных строк. В ней обязательно должны быть общие боковые и верхние заголовки. Еще одной особенностью статистической таблицы является наличие подлежащего (характеристика статистической совокупности) и сказуемого (показатели, характеризующие совокупности).
Статистические таблицы являются наиболее рациональной формой изложения результатов сводки или группировки.
Слайд 283.3. Статистические таблицы
Подлежащее таблицы представляет ту статистическую совокупность, о которой идет речь
3.3. Статистические таблицы
Подлежащее таблицы представляет ту статистическую совокупность, о которой идет речь

Сказуемое таблицы - это те показатели, с помощью которых дается характеристика явления, отображаемого в таблице. Подлежащее и сказуемое таблицы могут располагаться по-разному, главное, чтобы таблица была легко читаемой, компактной и легко воспринималась.
Слайд 293.3. Статистические таблицы
В статистической практике и исследовательских работах используются таблицы различной сложности.
3.3. Статистические таблицы
В статистической практике и исследовательских работах используются таблицы различной сложности.

Если в подлежащем таблицы содержится простой перечень каких-либо объектов или территориальных единиц, таблица называется простой.
В подлежащем простой таблицы нет каких-либо группировок статистических данных. Эти таблицы имеют самое широкое применение в статистической практике, например характеристика городов РФ по численности населения, средней зарплате и т. п.
Если подлежащее простой таблицы содержит перечень территорий, например областей, краев, автономных округов, республик и т. д., то такая таблица называется территориальной.
Простая таблица содержит только описательные сведения, ее аналитические возможности ограничены. Глубокий анализ исследуемой совокупности, взаимосвязей признаков предполагает построение более сложных таблиц - групповых и комбинационных.
Слайд 303.3. Статистические таблицы
Групповые таблицы в отличие от простых содержат в подлежащем не
3.3. Статистические таблицы
Групповые таблицы в отличие от простых содержат в подлежащем не

Простейшим видом групповой таблицы являются таблицы, в которых представлены ряды распределения (см. табл. 3.6). Групповая таблица может быть более сложной, если в сказуемом приводится не только число единиц в каждой группе, но и ряд других важных показателей, количественно и качественно характеризующих группы подлежащего. Такие таблицы часто используются в целях сопоставления обобщающих показателей по группам, что позволяет сделать определенные практические выводы. Более широкими аналитическими возможностями располагают комбинационные таблицы.
Комбинационные таблицы - таблицы, в подлежащем которых группы единиц, образованные по одному признаку, подразделяются на подгруппы по одному или нескольким признакам.
В отличие от простых и групповых таблиц комбинационные позволяют проследить зависимость показателей сказуемого от нескольких признаков, которые легли в основу комбинационной группировки в подлежащем.
Слайд 313.3. Статистические таблицы
Наряду с перечисленными выше таблицами в статистической практике применяют таблицы
3.3. Статистические таблицы
Наряду с перечисленными выше таблицами в статистической практике применяют таблицы

В основе построения таких таблиц лежит группировка единиц совокупности по двум или более признакам, которые называются уровнями. Например, население делится по полу (мужской, женский) и т. п. Таким образом, признак А имеет n градаций (или уровней): A1, A2, An (в нашем примере n = 2). Далее изучается взаимодействие признака А с другим признаком - В, который подразделяется на m градаций (факторов): B1, B2, Bm. В нашем примере признак В - принадлежность к какой-либо профессии, а B1, B2, Bm принимают конкретные значения (доктор, водитель, учитель, строитель и т. д.). Группировка по двум и более признакам используется для оценки взаимосвязей между признаками А и В.
Результаты наблюдений можно представить таблицей сопряженности, состоящей из n строк и m столбцов, в ячейках которых проставлены частоты событий nij, т. е. количество объектов выборки, обладающих комбинацией уровней Aj и Bj. Если между переменными A и B имеется взаимно-однозначная прямая или обратная функциональная связь, то все частоты nij концентрируются по одной из диагоналей таблицы. При не столь сильной связи некоторое число наблюдений попадает и на недиагональные элементы. В этих условиях перед исследователем стоит задача: выяснить, насколько точно можно предсказать значение одного признака по величине другого.
Таблица частот называется одномерной, если в ней табулирована только одна переменная.
Таблица, в основе которой лежит группировка по двум признакам (уровням), которые табулируются по двум признакам (факторам), называется таблицей с двумя входами.
Таблицы частот, в которых табулируются значения двух или более признаков, называются таблицами сопряженности.
Слайд 323.3. Статистические таблицы
Из всех видов статистических таблиц наиболее широкое применение имеют простые
3.3. Статистические таблицы
Из всех видов статистических таблиц наиболее широкое применение имеют простые

Форма статистической таблицы должна наилучшим образом отвечать сущности выражаемого ею явления и целям его изучения. Это достигается путем соответствующей разработки подлежащего и сказуемого таблицы.
Внешне таблица должна быть небольшой и компактной, иметь название, указание единиц измерения, а также времени и места, к которым относятся сведения. Заголовки строк и граф в таблице даются кратко, но четко. Чрезмерное загромождение таблицы цифровыми данными, неряшливое оформление затрудняют ее чтение и анализ.
Слайд 333.3. Статистические таблицы
Основные правила построения статистических таблиц:
• таблица должна быть компактной и
3.3. Статистические таблицы
Основные правила построения статистических таблиц:
• таблица должна быть компактной и

• заголовок таблицы, названия граф и строк должны быть четкими, краткими, лаконичными. В заголовке должны быть отражены объект, признак, время и место совершения события;
• графы и строки следует нумеровать;
• графы и строки должны содержать единицы измерения, для которых существуют общепринятые сокращения;
• информацию, сопоставляемую в ходе анализа, лучше всего располагать в соседних графах (либо одну под другой). Это облегчает процесс сравнения;
Слайд 343.3. Статистические таблицы
Основные правила построения статистических таблиц:
• для удобства чтения и работы
3.3. Статистические таблицы
Основные правила построения статистических таблиц:
• для удобства чтения и работы

• числа целесообразно округлять с одинаковой степенью точности (до целого знака, до десятой доли);
• отсутствие данных обозначается знаком умножения (х), если данная позиция не подлежит заполнению, отсутствие сведений обозначается многоточием (...), либо «н. д.», либо «н. св.», при отсутствии явления ставится знак тире (-);
• для отображения очень малых чисел используют обозначение 0.0 или 0.00;
• если число получено на основании условных расчетов, то его берут в скобки, сомнительные числа сопровождают вопросительным знаком, а предварительные - знаком (*).
Слайд 353.3. Статистические таблицы
В случае необходимости дополнительной информации статистические таблицы сопровождаются сносками и
3.3. Статистические таблицы
В случае необходимости дополнительной информации статистические таблицы сопровождаются сносками и

Сносками пользуются для того, чтобы указать на ограниченные обстоятельства, которые надо принять во внимание при чтении таблицы.
При соблюдении этих правил статистическая таблица становится основным средством представления, обработки и обобщения статистической информации о состоянии и развитии изучаемых социально-экономических явлений.
Слайд 363.4. Графические представления статистической информации
Полученные в результате сводки или статистического анализа в
3.4. Графические представления статистической информации
Полученные в результате сводки или статистического анализа в

Использование графиков для представления статистической информации позволяет придать статистическим данным наглядность и выразительность, облегчить их восприятие, а во многих случаях и анализ. Многообразие графических представлений статистических показателей дает огромные возможности для наиболее выразительной демонстрации явления или процесса.
Графики - условные изображения числовых величин и их соотношений в виде различных геометрических образов: точек, линий, плоских фигур и т. п.
Статистический график позволяет сразу оценить характер изучаемого явления, присущие ему закономерности и особенности, тенденции развития, взаимосвязь характеризующих его показателей.
Слайд 373.4. Графические представления статистической информации
Каждый график состоит из графического образа и вспомогательных
3.4. Графические представления статистической информации
Каждый график состоит из графического образа и вспомогательных

Графический образ - совокупность точек, линий и фигур, с помощью которых изображаются статистические данные.
Вспомогательные элементы - общее название графика, оси координат, шкалы, числовые сетки и числовые данные, дополняющие и уточняющие изображаемые показатели. Вспомогательные элементы облегчают чтение графика и его истолкование.
Название графика должно кратко и точно раскрывать его содержание. Пояснительные тексты могут располагаться в пределах графического образа или рядом с ним либо выноситься за его пределы.
Слайд 383.4. Графические представления статистической информации
Оси координат с нанесенными на них шкалами и
3.4. Графические представления статистической информации
Оси координат с нанесенными на них шкалами и

Шкалы могут быть прямолинейными или криволинейными (круговыми), равномерными (линейными) и неравномерными. Иногда целесообразно применять так называемые сопряженные шкалы, построенные на одной или двух параллельных линиях. Чаще всего одна из сопряженных шкал используется для отсчета абсолютных величин, а вторая - соответствующих им относительных.
Числа на шкалах проставляются равномерно, при этом последнее число должно превышать максимальный уровень показателя, значение которого отсчитывается по этой шкале.
Числовая сетка, как правило, должна иметь базовую линию, роль которой обычно играет ось абсцисс.
Слайд 393.4. Графические представления статистической информации
По содержанию, или назначению, можно выделить:
графики сравнения в
3.4. Графические представления статистической информации
По содержанию, или назначению, можно выделить:
графики сравнения в

графики различных относительных величин (структуры, динамики и др.);
графики вариационных рядов; графики размещения по территории; графики взаимосвязанных показателей и т. д.
Слайд 403.4. Графические представления статистической информации
По способу построения графики можно разделить на диаграммы
3.4. Графические представления статистической информации
По способу построения графики можно разделить на диаграммы

Диаграммы - наиболее распространенный способ графических изображений. Это графики количественных отношений. Виды и способы их построения разнообразны. Диаграммы применяются для наглядного сопоставления в различных аспектах (пространственном, временном и др.) независимых друг от друга величин: территорий, населения и т. д. При этом сравнение исследуемых совокупностей производится по какому-либо существенному варьирующему признаку.
Статистические карты - графики количественного распределения по поверхности. По своей основной цели они близко примыкают к диаграммам и специфичны лишь потому, что представляют собой условные изображения статистических данных на контурной географической карте, т. е. показывают пространственное размещение или пространственную распространенность статистических данных.
Слайд 413.4. Графические представления статистической информации
В зависимости от круга решаемых задач выделяются диаграммы
3.4. Графические представления статистической информации
В зависимости от круга решаемых задач выделяются диаграммы

Каждый столбик изображает величину отдельного уровня исследуемого статистического ряда. Таким образом, сравнение статистических показателей возможно потому, что все сравниваемые показатели выражены в одной единице измерения.
Слайд 423.4. Графические представления статистической информации
Статистические карты представляют собой вид графических изображений статистических
3.4. Графические представления статистической информации
Статистические карты представляют собой вид графических изображений статистических

Средствами изображения территориального размещения являются штриховка, фоновая раскраска или геометрические фигуры. Различают картограммы и картодиаграммы.
Картограммы - это схематическая географическая карта, на которой штриховкой различной густоты, точками или окраской определенной степени насыщенности показывается сравнительная интенсивность какого-либо показателя в пределах каждой единицы нанесенного на карту территориального деления (например, плотность населения по областям или республикам, распределения районов по урожайности зерновых культур и т. п.). Картограммы делятся на фоновые и точечные.
Картограмма фоновая - вид картограммы, на которой штриховкой различной густоты или окраской определенной степени насыщенности показывают интенсивность какого-либо показателя в пределах территориальной единицы.
Картограмма точечная - вид картограммы, где уровень выбранного явления изображается с помощью точек. Точка изображает одну единицу в совокупности или некоторое их количество, показывая на географической карте плотность или частоту проявления определенного признака.



 Математическая статистика результатов ЕГЭ
Математическая статистика результатов ЕГЭ Теорема о свойстве биссектрисы с доказательством
Теорема о свойстве биссектрисы с доказательством Задачи. Диаграмма
Задачи. Диаграмма Вариационно-статистический метод анализа
Вариационно-статистический метод анализа Элементы статистической обработки данных
Элементы статистической обработки данных Брейн-ринг. Геометрия
Брейн-ринг. Геометрия Геометрический смысл производной f '(x₀) = tg α = к
Геометрический смысл производной f '(x₀) = tg α = к Ломаная. Длина ломаной
Ломаная. Длина ломаной Многогранники. Розв'язування задач
Многогранники. Розв'язування задач Таблица умножения. Анимированная сорбонка
Таблица умножения. Анимированная сорбонка Прямоугольный параллелепипед
Прямоугольный параллелепипед Изоморфные графы
Изоморфные графы Случайный выбор точки из отрезка
Случайный выбор точки из отрезка Равенство, неравенство. Устный счет (1 класс)
Равенство, неравенство. Устный счет (1 класс) З історії геометрії
З історії геометрії Линейная алгебра. Лекция №2. Часть 2
Линейная алгебра. Лекция №2. Часть 2 Правила комбинаторики. Основные понятия
Правила комбинаторики. Основные понятия Презентация на тему ОБЪЁМ ТЕЛ
Презентация на тему ОБЪЁМ ТЕЛ  Разминка. Линейная функция
Разминка. Линейная функция задачи
задачи Решение систем линейных неравенств
Решение систем линейных неравенств Оценочная и сравнительная классификация алгоритмов
Оценочная и сравнительная классификация алгоритмов Свойства точек числовой окружности
Свойства точек числовой окружности Задачи про форматы листов. Решение практико-ориентированных задач
Задачи про форматы листов. Решение практико-ориентированных задач Теорема о трех перпендикулярах
Теорема о трех перпендикулярах Множества. (Задачи)
Множества. (Задачи) Основи векторної графіки
Основи векторної графіки Интеграл, интеграция, интегрирование. Решение задач
Интеграл, интеграция, интегрирование. Решение задач