Содержание
- 3. МНИМАЯ ЕДИНИЦА
- 5. Мнимые числа i = -1, i – мнимая единица i, 2i, -0,3i — чисто мнимые числа
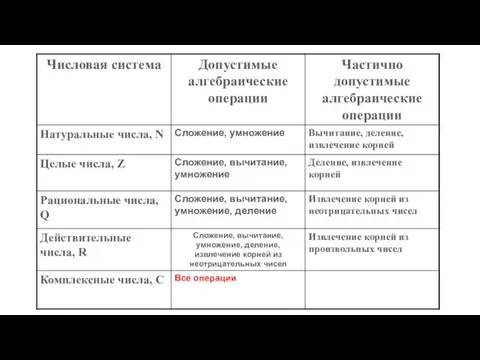
- 7. Комплéксные числа форма записи: алгебраическая, тригонометрическая экспоненциальная (показательная) Числа вида a + bi, где a и
- 9. Комплексные числа Определение 1. Комплексным числом называют сумму действительного числа и чисто мнимого числа. Определение 2.
- 10. Решение. Используя условие равенства комплексных чисел имеем 2y = 13, 4x = – 6, тогда Найти
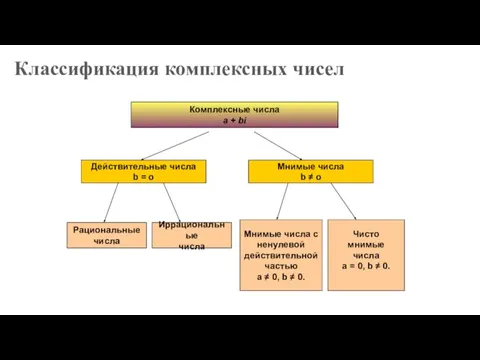
- 11. Классификация комплексных чисел Комплексные числа a + bi Действительные числа b = o Мнимые числа b
- 12. Арифметические операции над комплексными числами (а + bi) + (c + di) = (а + с)
- 13. Сопряженные комплексные числа Определение: Если у комплексного числа сохранить действительную часть и поменять знак у мнимой
- 14. z1 = 12 + 3i, z2 = 5 – 7i. Найти: а) z1 + z2; б)
- 15. (5 + 3i)(5 – 3i) (2 + 3i)(5 – 7i) (2 – 7i)2 = = =
- 16. = = =
- 17. = = = 2
- 18. Модуль комплексного числа Определение: Модулем комплексного числа z = a + bi называют неотрицательное число
- 19. Геометрическое изображение комплексных чисел. Комплексному числу z на координатной плоскости соответствует точка М(a, b). Часто вместо
- 20. Тригонометрическая форма комплексного числа где φ – аргумент комплексного числа, r = модуль комплексного числа,
- 22. Скачать презентацию


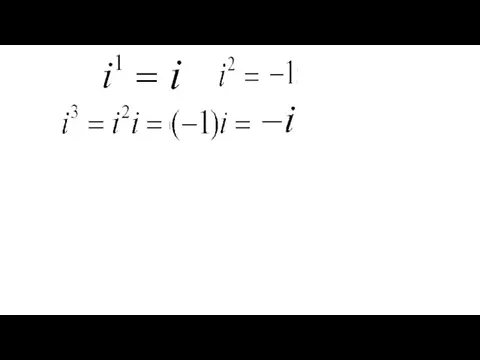

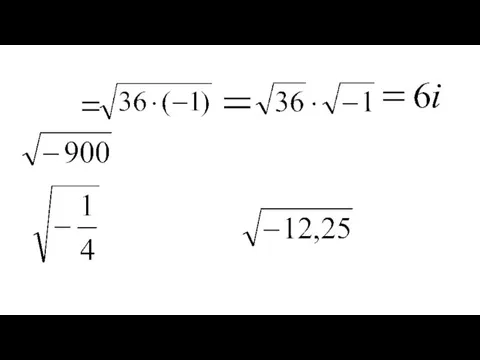






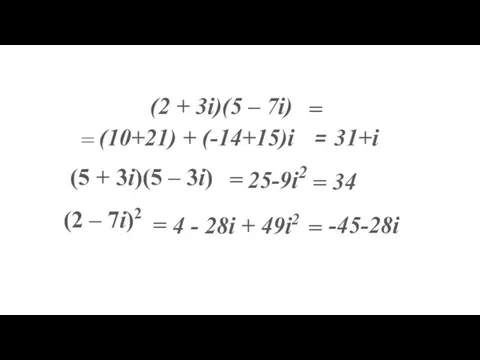
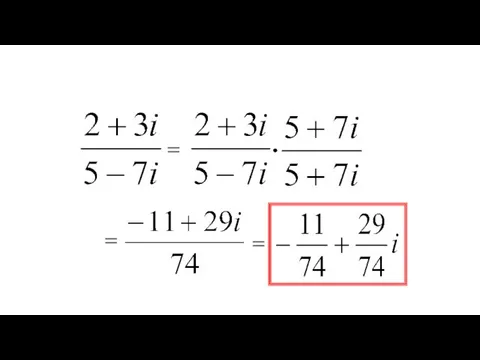
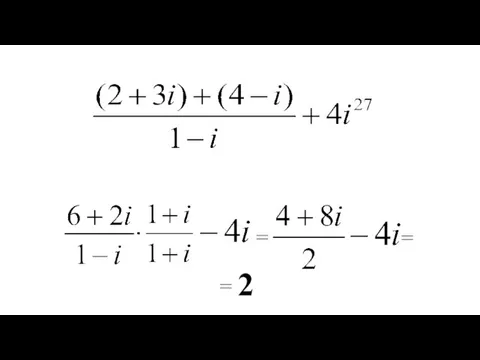



 Преобразование целого выражения в многочлен
Преобразование целого выражения в многочлен Длиннее, короче, одинаковые по длине. Математическая сказка
Длиннее, короче, одинаковые по длине. Математическая сказка Решение задач
Решение задач Решение систем линейных уравнений методом Гаусса
Решение систем линейных уравнений методом Гаусса Усеченные фигуры
Усеченные фигуры Умножение одночлена на многочлен
Умножение одночлена на многочлен Элементы комбинаторики
Элементы комбинаторики Парадокс раздела ставки
Парадокс раздела ставки Интерактивный плакат: Многогранники
Интерактивный плакат: Многогранники Тема: Письменное умножение на двузначное число. Закрепление.
Тема: Письменное умножение на двузначное число. Закрепление. Метод Гаусса решения систем линейных уравнений
Метод Гаусса решения систем линейных уравнений Пример проектной работы. Зимние олимпийские игры. Общая статистика
Пример проектной работы. Зимние олимпийские игры. Общая статистика Теорема Гаусса-Остроградского
Теорема Гаусса-Остроградского Рационал бөлшектер
Рационал бөлшектер Переменная из формулы
Переменная из формулы Сантиметр - единица измерения длины
Сантиметр - единица измерения длины Презентация на тему Центральная и осевая симметрии в природе
Презентация на тему Центральная и осевая симметрии в природе  Вычисление углов между прямыми и плоскостями
Вычисление углов между прямыми и плоскостями Второй признак подобия треугольников
Второй признак подобия треугольников Вычисление значений выражений содержащих аркфункции от функции
Вычисление значений выражений содержащих аркфункции от функции Деление круглых сотен на число 100
Деление круглых сотен на число 100 Теория вероятностей
Теория вероятностей Прогрессия. Алгебраический анзац
Прогрессия. Алгебраический анзац Основные понятия комбинаторики и теории вероятностей
Основные понятия комбинаторики и теории вероятностей Множества. Операции над ними. Комбинаторика
Множества. Операции над ними. Комбинаторика Решение уравнений и неравенств. Линейные уравнения и неравенства
Решение уравнений и неравенств. Линейные уравнения и неравенства Тренажер. Смешарики. Сложение в пределах 20
Тренажер. Смешарики. Сложение в пределах 20 Решение задач
Решение задач