Содержание
- 2. Лекция 7
- 3. Повторение испытаний
- 4. Определение сложного эксперимента Рассмотрим единичный эксперимент, в результате которого может произойти некоторое событие А. Если событие
- 5. Основные вопросы 1. Вероятность для некоторого числа появлений события А; 2. Вероятность для числа проведенных испытаний
- 6. Типы испытаний 1. Вероятность успеха постоянна в каждом испытании; 2. Вероятность успеха меняется.
- 7. Схема Бернулли (биномиальная) Пусть производится n независимых испытаний. Пусть P(А)=p в каждом испытании и q =
- 8. Найти ={в n испытаниях событие А наступит k раз}
- 9. Вероятность события {в n испытаниях А наступит k раз и не наступит n – k раз}
- 10. Число таких событий равно Так как эти события несовместны и равновероятны, получаем Полученную формулу называют формулой
- 11. Пример 1 Университетом для студенческих общежитий приобретено 5 телевизоров. Для каждого из них вероятность выхода из
- 12. Решение Из условия задачи выпишем p, n, k, q. n=5; k=1; p=0,1; q=0,9. Тогда по формуле
- 13. Вероятность того, что расход электроэнергии в продолжении одних суток не превысит установленной нормы, равна р =
- 14. Решение р = 0,75. q = 1 – p = 1 – 0,75 = 0,25. Искомая
- 15. Схема Пуассона Пусть вероятность успеха при фиксированном числе испытаний n постоянна и мала, уменьшается с ростом
- 16. Формула Пуассона
- 17. Пример 1 Вероятность того, что какой-нибудь абонент позвонит на коммутатор в течение часа, равна 0,01. Телефонная
- 18. Решение По условию задачи p=0,01; n=300; k=4. Найдем λ=300⋅0,01=3 По формуле Пуассона
- 19. Пример 2 Найти вероятность не более двух успехов в схеме Пуассона при
- 20. Решение
- 21. Геометрическая схема Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р
- 22. Основной вопрос Пусть в первых k – 1 испытаниях событие А не наступило, а в k-м
- 23. Пример Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель р =
- 24. Решение Из условия задачи выпишем р = 0,6; q = 0,4; k = 3.
- 25. Пользоваться формулой Бернулли при больших значениях n достаточно трудно. Например, если n=5000, k=3000,p=0,1, то для отыскания
- 26. Теорема Пуассона Пусть в схеме Бернулли n велико, p мало и npq
- 27. Пример Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна
- 28. Решение n = 5000, р = 0,0002, к = 3.
- 29. Локальная теорема Лапласа Если вероятность р появления события А в каждом испытании постоянна, отлична от нуля
- 30. Функция называется функцией Гаусса.
- 31. Свойства функции Гаусса 1. Четность 2. Асимптотичность
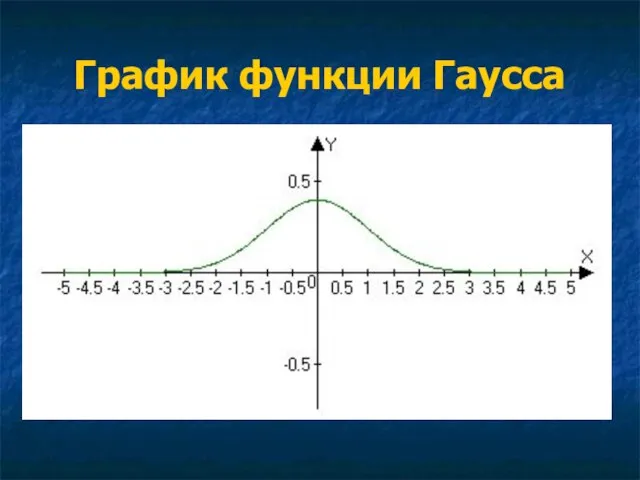
- 32. График функции Гаусса
- 33. Пример Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность
- 34. Решение n = 400;k = 80; p = 0,2; q = 0,8.
- 35. По таблице находим: Искомая вероятность:
- 36. Пример Вероятность поражения мишени стрелком при одном выстреле р = 0,75. Найти вероятность того, что при
- 37. Решение По условию, n = 10; k = 8; p = 0.75; q = 0,25.
- 38. По таблице : Искомая вероятность: Формула Бернулли приводит к другому результату, а именно:
- 39. Интегральная теорема Лапласа Как вычислить вероятность того, что событие А появится в n испытаниях не менее
- 40. Интегральная Теорема Лапласа
- 41. Функция Лапласа
- 42. Свойства функции Лапласа 1. Нечетность 2. Асимптотичность
- 43. Пример Вероятность того, что деталь не прошла проверку, равна р=0,2. Найти вероятность того, что среди 400
- 44. Решение По условию, р = 0,2; q = 0.8; n = 400;
- 46. По таблице находим: Искомая вероятность
- 47. Наивероятнейшее число успехов в схеме Бернулли
- 48. Пример Монета бросается 100 раз. Найти наивероятнейшее число выпадений герба.
- 49. Задачи
- 50. Задача 1 Вероятность выигрыша в одной партии равна 0,5. Найти вероятность выигрыша менее 2-х партий из
- 51. Решение Из условия задачи n=4; k=2; p=q=0,5. Менее 2-х из 4-х партий по формуле Бернулли
- 52. Задача 2 Вероятность попадания стрелком при одном выстреле 0,3. Стрелок делает 10 выстрелов. Найти вероятность, что
- 53. Решение По условию задачи находим n=10; k=7; p=0,3; q=0,7. По формуле Бернулли (не менее 7 из
- 54. Задача 3 В результате обследования были выявлены семьи, имеющие по четыре ребенка. Считая вероятности появления мальчика
- 55. Решение Вероятность появления мальчика и девочки равна p=1/2; n=4; k=2; q=1/2. По формуле Бернулли вероятность появления
- 56. Задача 4 Четыре покупателя приехали на оптовый склад. Вероятность того, что каждому из этих покупателей потребуется
- 57. Решение По условию задачи n=4; k=2; p=0,4; q=0,6. Вероятность, что холодильник потребуется не менее чем двум
- 58. Задача 5 В новом микрорайоне поставлено 10000 кодовых замков на входных дверях домов. Вероятность выхода из
- 59. Решение В задаче n=10000; p=0,0002. Используя формулу Пуассона найдем λ=np=10000⋅0,0002=2; Вероятность, что откажут два замка
- 60. Вероятность, что откажут три замка Вероятность, что откажут пять замков
- 61. Задача 6 Всхожесть семян огурцов равна 0,8. Какова вероятность того, что из пяти посеянных семян взойдут
- 62. Решение В задаче n=5; k=4; p=0,8; q=0,2. По формуле Бернулли имеем
- 63. Задача 7 Найти вероятность того, что если бросить монету 200 раз, то орел выпадет от 90
- 64. Решение Вероятность выпадения орла/решки p=q=0,5; n=200; k1=90; k2=110. По интегральной теореме Лапласа:
- 65. Найдем
- 66. Задача 8 В жилом доме имеется 6400 ламп. Вероятность включения каждой из них в вечернее время
- 67. Решение n=6400; k1=3120; k2=3200; p=q=0,5. По интегральной теореме Лапласа имеем:
- 69. Задача 9 Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100
- 70. Решение По условию задачи n=100; p=0,8; q=0,2; k=75. Вероятность, что мишень будет поражена ровно 75 раз
- 72. Разбор варианта контр. работы №1
- 73. Задача 1 Из 10 человек в группе 2 студента изучают английский, 5 – французский, 3 –
- 74. Решение
- 75. Задача 2 В партии из 17 деталей есть 9 стандартных. Наудачу отобраны 9 деталей. Найти вероятность,
- 76. Решение А={ровно 4 cтанд. Среди 9-ти отобранных}
- 77. Задача 3 Двое договорились о встрече между 8 и 9 часами утра, причем ждать не более
- 78. Решение
- 79. Задача 4 Фирма участвует в трех независимых проектах, вероятности успеха которых составляют 0,9; 0,4; 0,8. Найти
- 80. Решение «хотя бы два»= « только два» + «все три»
- 81. Задача 5 В продуктовом магазине было проведено исследование продаж некот. товара. Оказалось, что этот товар покупает
- 82. Решение
- 83. Задача 6 Вероятность попадания в цель при одном выстреле равна 0,4. Сделано 6 выстрелов. Найти вероятность
- 84. Решение p=0,4 q=0,6 n=6 k
- 85. Вопросы к лекции 7 Формула Бернулли Формула Пуассона Локальная теорема Лапласа Интегральная теорема Лапласа Наивероятнейшее число
- 87. Скачать презентацию




























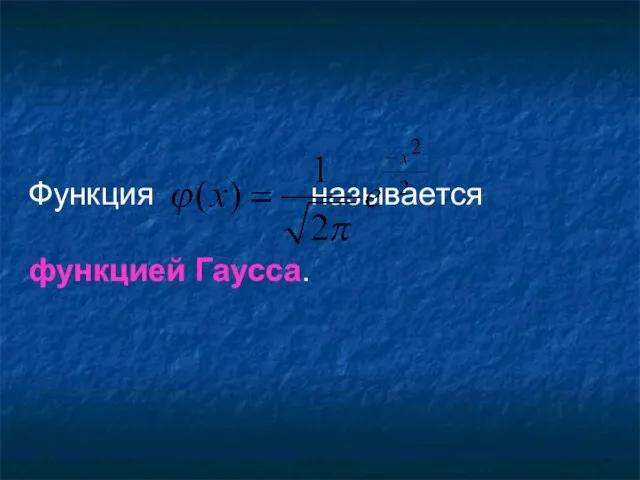




































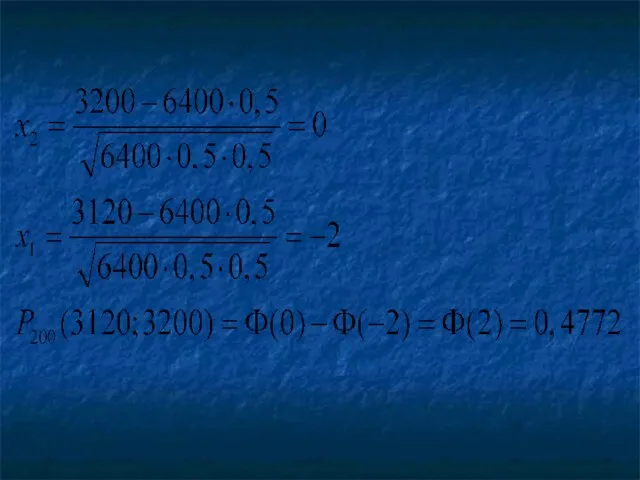


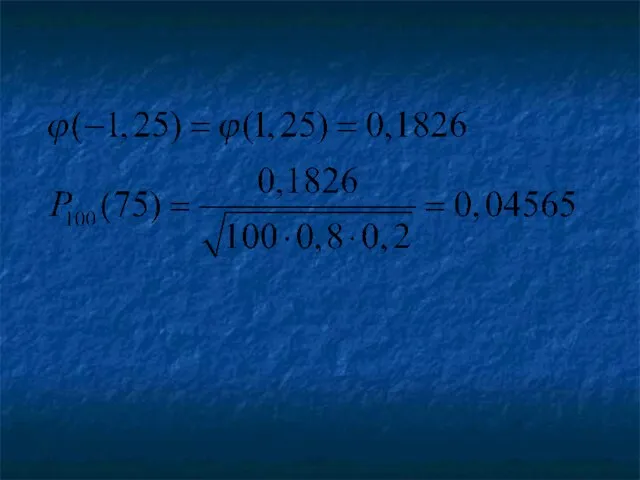














 Диаграммы
Диаграммы Операции над множествами
Операции над множествами Задания с фигурами
Задания с фигурами Математика для дошкольников (средняя группа)
Математика для дошкольников (средняя группа) Умножение одночленов. Возведение одночлена в степень
Умножение одночленов. Возведение одночлена в степень Статистика. Статистика знает всё (Ильф и Петров). Выборочные исследования
Статистика. Статистика знает всё (Ильф и Петров). Выборочные исследования Теория вероятностей. Задачи
Теория вероятностей. Задачи Тренажер Состав числа
Тренажер Состав числа Тела вращения
Тела вращения Великие математики древности
Великие математики древности Арифметические операции в разных системах счисления
Арифметические операции в разных системах счисления Практикум по решению задач практической направленности
Практикум по решению задач практической направленности Проценты и десятичные дроби
Проценты и десятичные дроби Умножение для ленивых? 5 класс
Умножение для ленивых? 5 класс Вписанная и описанная окружность
Вписанная и описанная окружность Слагаемые. Сумма
Слагаемые. Сумма Понятие многогранника
Понятие многогранника Последовательности. Золотое сечение
Последовательности. Золотое сечение Линейные пространства и линейные операторы. Лекция 4
Линейные пространства и линейные операторы. Лекция 4 Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Перспективная модель ЕГЭ по математике
Перспективная модель ЕГЭ по математике Число и цифра 5
Число и цифра 5 Теорема о трёх перпендикулярах
Теорема о трёх перпендикулярах Задачи на пропорциональное деление
Задачи на пропорциональное деление Преобразование тригонометрических выражений
Преобразование тригонометрических выражений Формирование элементарных математических представлений (игра)
Формирование элементарных математических представлений (игра) Квадратные уравнения и знаки его корней
Квадратные уравнения и знаки его корней Случаи вычитания 15 -
Случаи вычитания 15 -