Множества

Основная учебная литература
Шершнев В.Г. Математический анализ. Режим доступа: http://znanium.com/bookread2.php?book=342089
Шершнев В.Г. Математический анализ: сборник задач с решениями. Режим доступа: http://znanium.com/bookread2.php?book=501529#
Дополнительная учебная литература
Шипачев В.С. Высшая математика: Учебник. Режим доступа: http://znanium.com/bookread2.php?book=469720
Шипачев В.С. Задачник по высшей математике. – Режим доступа: http://znanium.com/bookread2.php?book=470407
Рудык Б. М. Курс высшей математики для экономистов. – Режим доступа: http://znanium.com/bookread2.php?book=512518#

Главы:
Элементы теории множеств
Введение в анализ
Дифференциальное исчисление функции одной переменной

Глава 1. Элементы теории множеств.
§1. Основные понятия.

Множество?

Множество?
В математике некоторые понятия являются первичными, неопределяемыми.
К таким понятиям относится «множество».
Оно не определяется через другие понятия, его поясняют на примерах.

Множество?
«Множество есть многое, мыслимое нами как единое». Основоположник теории множеств немецкий математик Георг Кантор (1845-1918)

Множество — это совокупность элементов, объединенных общим (характеристическим) свойством.
Объекты, из которых состоит множество, называют его элементами.
Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.

Обозначения:
A, B, C,…, X, Y, Z — множества;
a, b, c,…, x, y, z — элементы множеств;
x∈A — обозначает принадлежность элемента х множеству А;
x∉ A — x не принадлежит множеству А.

Кванторы:
⇒ — следовательно, если … то;
⇔ — тогда и только тогда, необходимо и достаточно;
∀— любой, каждый;
— существует.
Выражение читается так:
существует элемент x множества X, обладающий свойством P(x).

§2. Способы задания множеств

Перечислением элементов.
Например, Х = {1, 2} — множество Х состоит из двух элементов: 1 и 2.

Указанием характеристического свойства.
Например,
X={x: (x−1)(x+3)=0} — это множество содержит два элемента — корни уравнения (x−1)(x+3) = 0,
то есть числа 1 и −3.

Указанием характеристического свойства.
Например,
А={(λ1, … , λn) : λ12 + λ22 + … + λn2 = 0} – такое множество содержит единственный набор чисел, состоящий из n нулей, т. е. А={(0, 0, … , 0)}.

Пустое множество – это множество, не содержащее ни одного элемента.
∀х х ∉ ∅.
Универсальное множество – это множество, содержащее все элементы.
∀х х ∈ U.

Пустое множество – это множество, не содержащее ни одного элемента.
Универсальное множество – это множество, содержащее все элементы.
ПРИМЕР.
{x ∈ R : x2 < 0} = ∅. {x ∈ R : x2 ≥ 0} = R = U.

Множество А называется подмножеством множества В, если каждый элемент множества А является элементом множества В:
А ⊂ В ⇔ (х ∈ А ⇒ х ∈ В)
Очевидно, что ∅ ⊂ А, А ⊂ А, А ⊂ U для любого множества А.

Множества А и В называются равными, если каждый элемент множества А является элементом множества В и, наоборот, каждый элемент множества В является элементом множества А:
А = В ⇔ А ⊂ В и В ⊂ А.

§3. Операции над множествами

При графическом изображении множеств удобно использовать круги Эйлера, на которых универсальное множество обычно представляют в виде прямоугольника, а остальные множества в виде овалов, заключенных внутри этого прямоугольника.

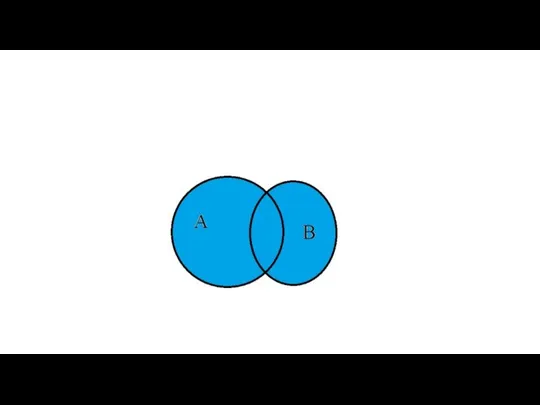
Объединением А∪В двух множеств А и В называется множество, состоящее из элементов, содержащихся либо в А, либо в В.
x∈A∪B ⇔ x∈A или x∈B;
x∉A∪B ⇔ x∉A и x∉B.

Найти объединение множеств А и В, если:
а) А={1, 2, 3, 4, 5}, В={2, 4, 6, 8, 10};

Найти объединение множеств А и В, если:
а) А={1, 2, 3, 4, 5}, В={2, 4, 6, 8, 10};
Ответ: А∪B={1, 2, 3, 4, 5, 6, 8, 10}

Найти объединение множеств А и В, если:
б) А={а, б, в, г, д, е}, В={а, в, д, к, и};

Найти объединение множеств А и В, если:
б) А={а, б, в, г, д, е}, В={а, в, д, к, и};
Ответ: А∪B={а, б, в, г, д, е, к, и}

Найти объединение множеств А и В, если:
в) А={а, в, д, ж, и, м, н, о}, В={в, к, и, о, м, п, с, ф};

Найти объединение множеств А и В, если:
в) А={а, в, д, ж, и, м, н, о}, В={в, к, и, о, м, п, с, ф};
Ответ: А∪B={а, в, д, ж, к, и, м, н, о, п, с, ф}

Найти объединение множеств А и В, если:
г) А={0, 1, 2, 3, 4, 5, 6, 7}, В={3, 4, 5, 6, 7, 8, 9, 10}.

Найти объединение множеств А и В, если:
г) А={0, 1, 2, 3, 4, 5, 6, 7}, В={3, 4, 5, 6, 7, 8, 9, 10}
Ответ: А∪B={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.

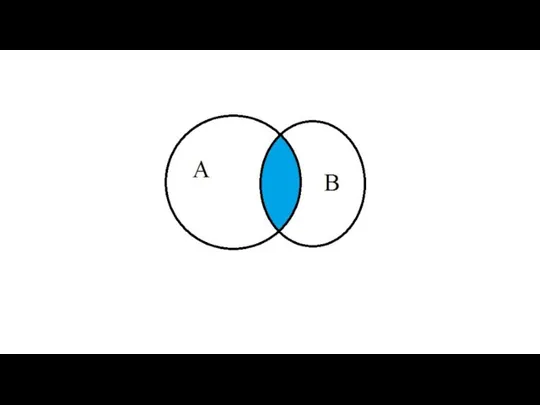
Пересечением А∩В двух множеств А и В называется множество, состоящее из элементов, содержащихся и в А, и в В.
x∈A∩B ⇔ x∈A и x∈B;
x∉A∩B ⇔ x∉A или x∉B.

Найти пересечение множеств А и В, если:
а) А={1, 2, 3, 4, 5}, В={2, 4, 6, 8, 10};

Найти пересечение множеств А и В, если:
а) А={1, 2, 3, 4, 5}, В={2, 4, 6, 8, 10};
Ответ: А∩B={2, 4}

Найти пересечение множеств А и В, если:
б) А={а, б, в, г, д, е}, В={а, в, д, к, и};

Найти пересечение множеств А и В, если:
б) А={а, б, в, г, д, е}, В={а, в, д, к, и};
Ответ: А∩B={а, в, д}

Найти пересечение множеств А и В, если:
в) А={а, в, д, ж, и, м, н, о}, В={в, к, и, о, м, п, с, ф};

Найти пересечение множеств А и В, если:
в) А={а, в, д, ж, и, м, н, о}, В={в, к, и, о, м, п, с, ф};
Ответ: А∩B={в, и, м, о}

Найти пересечение множеств А и В, если:
г) А={0, 1, 2, 3, 4, 5, 6, 7}, В={3, 4, 5, 6, 7, 8, 9, 10}.

Найти пересечение множеств А и В, если:
г) А={0, 1, 2, 3, 4, 5, 6, 7}, В={3, 4, 5, 6, 7, 8, 9, 10}
Ответ: А∩B={3, 4, 5, 6, 7}.

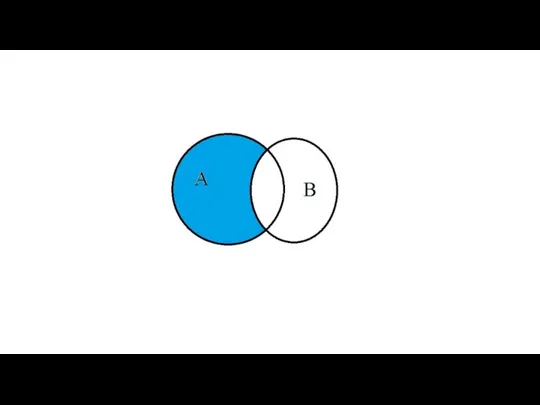
Разностью А \ В множеств А и В называется множество, состоящее из тех элементов множества А, которые не принадлежат множеству В.
x∈A\B ⇔ x∈A и x∉B;
x∉A\B ⇔ x∉A или x∈B.

Найти разность множеств А и В, если:
а) А={1, 2, 3, 4, 5}, В={2, 4, 6, 8, 10};
б) А={а, б, в, г, д, е}, В={а, в, д, к, и};
в) А={а, в, д, ж, и, м, н, о}, В={в, к, и, о, м, п, с, ф};
г) А={0, 1, 2, 3, 4, 5, 6, 7}, В={3, 4, 5, 6, 7, 8, 9, 10}.

Найти разность множеств А и В, если:
а) А={1, 2, 3, 4, 5}, В={2, 4, 6, 8, 10};
б) А={а, б, в, г, д, е}, В={а, в, д, к, и};
в) А={а, в, д, ж, и, м, н, о}, В={в, к, и, о, м, п, с, ф};
г) А={0, 1, 2, 3, 4, 5, 6, 7}, В={3, 4, 5, 6, 7, 8, 9, 10}
Ответ: а) А \ В ={1, 3, 5}, б) А \ В ={б, г, е},
в) А \ В ={а, д, ж, н}, г) А \ В ={0, 1, 2}.

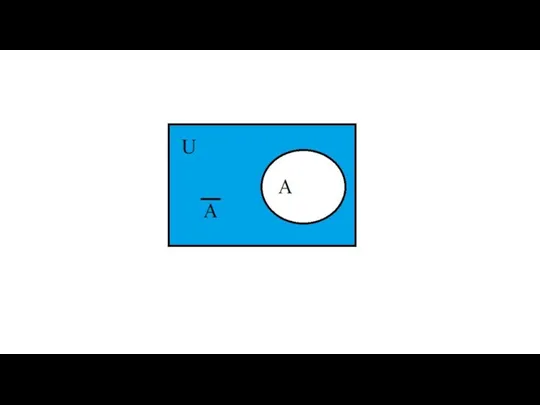
Разность U\A называется дополнением множества А и обозначается

Свойства операций:
1. A∪B=B∪A
2. A∩B=B∩A
3. A∪(B∪C)=(A∪B)∪C
4. A∩ (B∩C)=(A∩B)∩C
5. A∪(B∩C)=(A∪B)∩(A∪C)
6. A∩ (B∪C)=(A∩B)∪(A∩C)

Даны следующие числовые множества: А={1,3,5,7,9,11}, B={2,5,6,11,12}, C={1,2,3,5,9,12}. Найти множества, которые будут получены в результате выполнения следующих операций:
а) (А∪С)∩В; г) А∩B∩C;
б) (А∩С)\В; д) В\(А∩С);
в) (С\B)∪А; е) (B∩C)∪A.

ОТВЕТЫ:
Даны следующие числовые множества: А={1,3,5,7,9,11}, B={2,5,6,11,12}, C={1,2,3,5,9,12}. Найти множества, которые будут получены в результате выполнения следующих операций:
а) (А∪С)∩В={2, 5, 11, 12}; г) А∩B∩C={5};
б) (А∩С)\В={1, 3, 9}; д) В\(А∩С)={2, 6, 11, 12};
в) (С\B)∪А=A; е) (B∩C)∪A={1, 2, 3, 5, 7, 9, 11, 12}.

Заштрихуйте ту часть диаграммы, которая соответствует следующему множеству:
а) (А ∪ В) \ С;
б) (А ∪ В) ∩ (С ∪ В);
в) (А ∪ В) ∩ (С \ В);
г) (С \ В) ∪ (А \ С);
д) (А \ С) ∪ (В ∩ С);
е) (С ∪ А) \ (В ∩ А).

ОТВЕТЫ:
Заштрихуйте ту часть диаграммы, которая соответствует следующему множеству:
а) (А ∪ В) \ С;

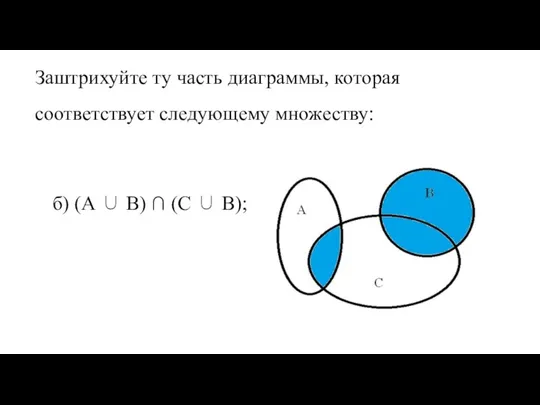
Заштрихуйте ту часть диаграммы, которая соответствует следующему множеству:
б) (А ∪ В) ∩ (С ∪ В);

Заштрихуйте ту часть диаграммы, которая соответствует следующему множеству:
в) (А ∪ В) ∩ (С \ В);

Заштрихуйте ту часть диаграммы, которая соответствует следующему множеству:
г) (С \ В) ∪ (А \ С);

Заштрихуйте ту часть диаграммы, которая соответствует следующему множеству:
д) (А \ С) ∪ (В ∩ С);

Заштрихуйте ту часть диаграммы, которая соответствует следующему множеству:
е) (С ∪ А) \ (В ∩ А).

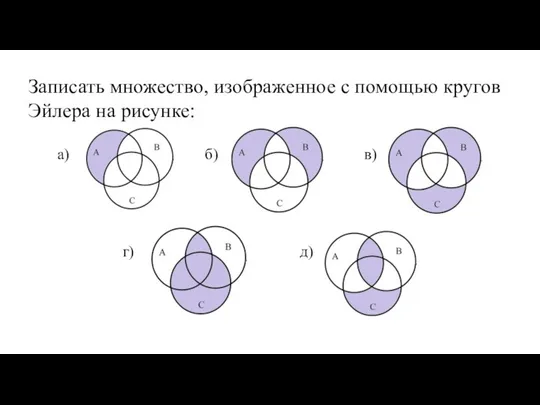
Записать множество, изображенное с помощью кругов Эйлера на рисунке:
а)
б)
г)
в)
д)

§4. Числовые множества