Комплексные числа. Определение множеств комплексных чисел

Числа (повторение)
Число – основное понятие математики.
Изучали:
Геометрическая иллюстрация чисел: точки на числовой прямой.
Каждому действительному числу соответствует точка на прямой;
каждая точка представляет действительное число;
установлено ВЗАИМНО-ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ между двумя множествами.

Определение множества комплексных чисел
надо с прямой выйти на плоскость
и рассмотреть каждую точку плоскости как изображение числа.
ОПРЕДЕЛЕНИЕ.
Для комплексных чисел определены действия:

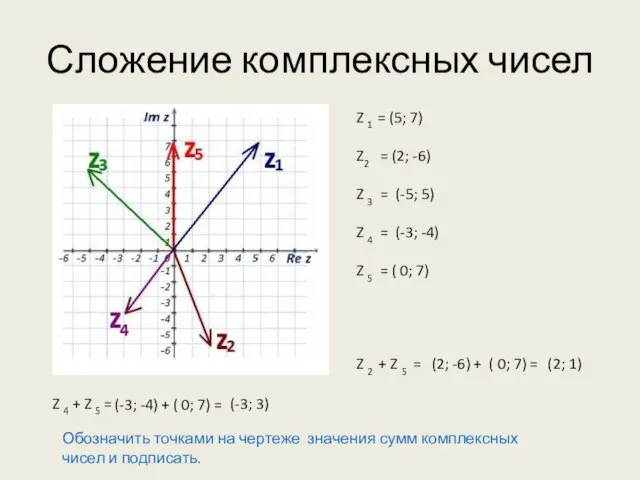
Сложение комплексных чисел
Z 1 = (5; 7)
Z2 = (2; -6)
Z 3 = (-5; 5)
Z 4 = (-3; -4)
Z 5 = ( 0; 7)
Z 2 + Z 5 =
(2; -6) + ( 0; 7) =
(2; 1)
Z 4 + Z 5 =
(-3; -4) + ( 0; 7) =
(-3; 3)
Обозначить точками на чертеже значения сумм комплексных чисел и подписать.

Понятие мнимой единицы
и

Алгебраическая форма записи
комплексного числа
Алгебраическая форма записи
комплексного числа

Сопряженное число
ПРИМЕР.
У сопряженного числа знак мнимой части меняется на противоположный.

два умножения
вместо деления!
если числитель и знаменатель умножить на число, сопряженное знаменателю, то получим: