Презентация на тему Решение простейших тригонометрических уравнений

Под простейшими тригонометрическими уравнениями понимают уравнения вида:
,где t – выражение с переменной, a∈.

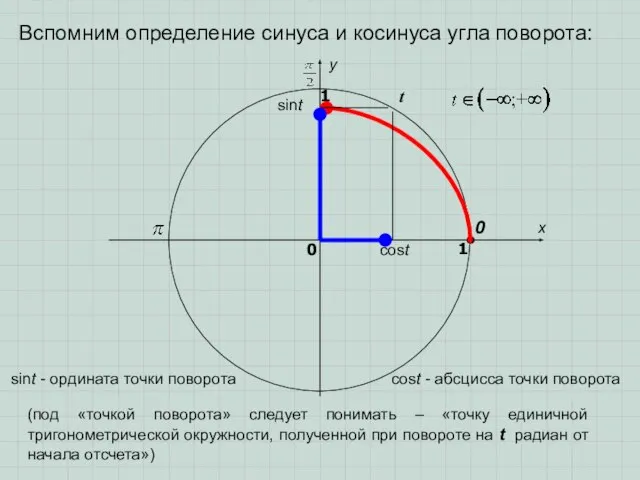
Вспомним определение синуса и косинуса угла поворота:
sint
cost
t
x
y
0
1
0
1
sint - ордината точки поворота
cost - абсцисса точки поворота
(под «точкой поворота» следует понимать – «точку единичной тригонометрической окружности, полученной при повороте на t радиан от начала отсчета»)

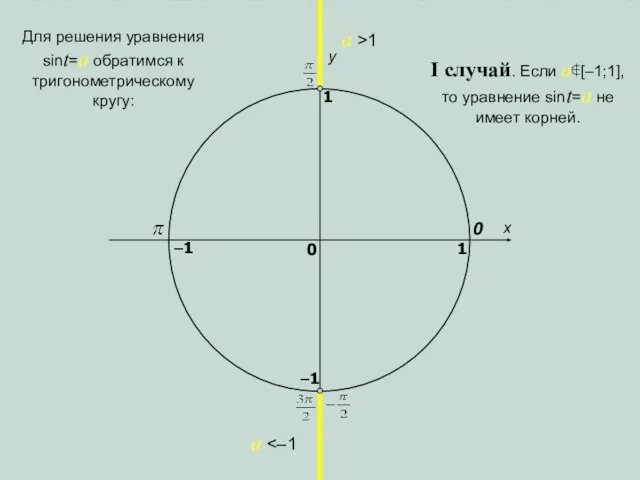
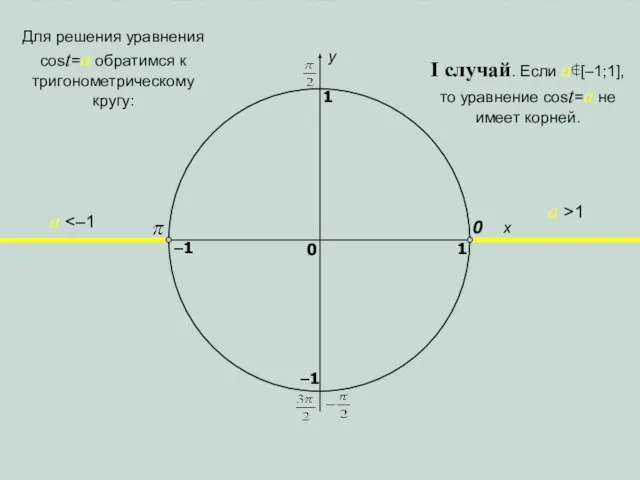
x
y
0
1
0
1
–1
–1
a >1
a <–1
I случай. Если a∉[–1;1], то уравнение sint=a не имеет корней.
Для решения уравнения sint=a обратимся к тригонометрическому кругу:

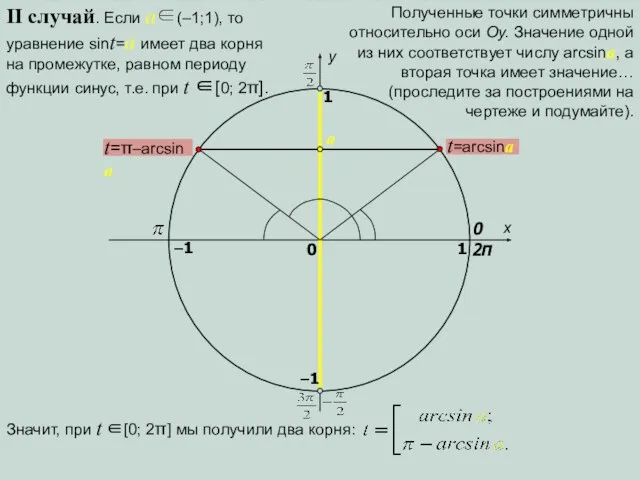
x
y
0
1
0
1
t=arcsina
t=π–arcsina
a
–1
–1
II случай. Если a∈(–1;1), то уравнение sint=a имеет два корня на промежутке, равном периоду функции синус, т.е. при t ∈[0; 2π].
Полученные точки симметричны относительно оси Оу. Значение одной из них соответствует числу arcsina, а вторая точка имеет значение… (проследите за построениями на чертеже и подумайте).
2π
Значит, при t ∈[0; 2π] мы получили два корня:

Учитывая периодичность функции синус, каждую из этих точек можно получить при добавлении целого числа полных поворотов, т.е.:
или
Можно заметить, что при наличии знака «+» перед arcsina к нему прибавляется четное(2k) число π, а при знаке «–» перед arcsina прибавляется нечетное(2m+1) число π. Поэтому эти два равенства можно объединить в одно и записать:
Эта формула позволяет найти корни простейшего тригонометрического уравнения sint=a в случаях, если a∈(–1;1).

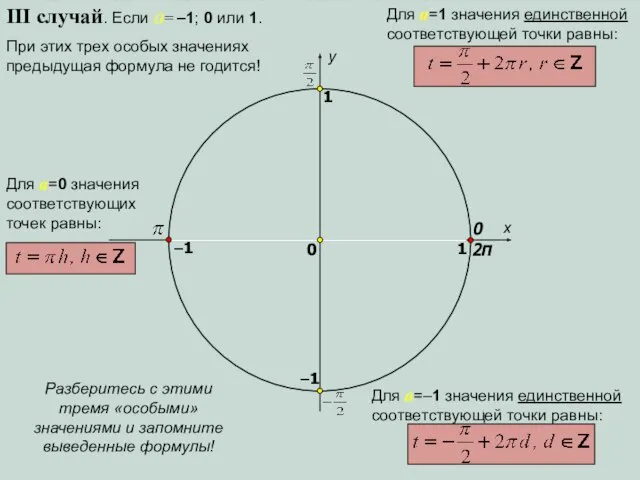
x
y
0
1
0
1
–1
–1
III случай. Если a= –1; 0 или 1.
При этих трех особых значениях предыдущая формула не годится!
2π
Для a=1 значения единственной соответствующей точки равны:
Для a=0 значения соответствующих точек равны:
Для a=–1 значения единственной соответствующей точки равны:
Разберитесь с этими тремя «особыми» значениями и запомните выведенные формулы!

x
y
0
1
0
1
–1
–1
a >1
a <–1
I случай. Если a∉[–1;1], то уравнение cost=a не имеет корней.
Для решения уравнения cost=a обратимся к тригонометрическому кругу:

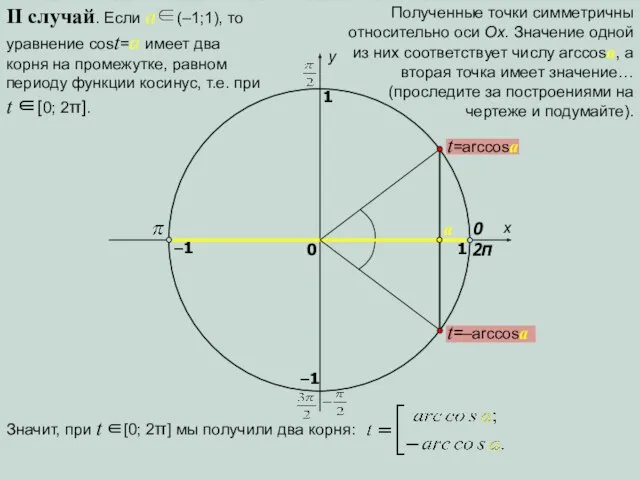
x
y
0
1
0
1
t=arccosa
t=–arccosa
a
–1
–1
II случай. Если a∈(–1;1), то уравнение cost=a имеет два корня на промежутке, равном периоду функции косинус, т.е. при t ∈[0; 2π].
Полученные точки симметричны относительно оси Оx. Значение одной из них соответствует числу arccosa, а вторая точка имеет значение… (проследите за построениями на чертеже и подумайте).
2π
Значит, при t ∈[0; 2π] мы получили два корня:

Учитывая периодичность функции косинус, каждую из этих точек можно получить при добавлении целого числа полных поворотов, т.е.:
Эти записи отличаются друг от друга только знаками перед arccosa. Поэтому эти два равенства можно объединить в одно и записать:
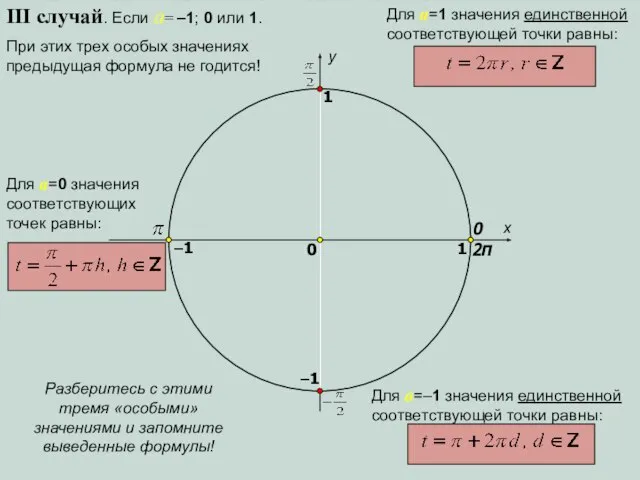
Эта формула позволяет найти корни простейшего тригонометрического уравнения cost=a в случаях, если a∈(–1;1).

x
y
0
1
0
1
–1
–1
III случай. Если a= –1; 0 или 1.
При этих трех особых значениях предыдущая формула не годится!
2π
Для a=1 значения единственной соответствующей точки равны:
Для a=0 значения соответствующих точек равны:
Для a=–1 значения единственной соответствующей точки равны:
Разберитесь с этими тремя «особыми» значениями и запомните выведенные формулы!

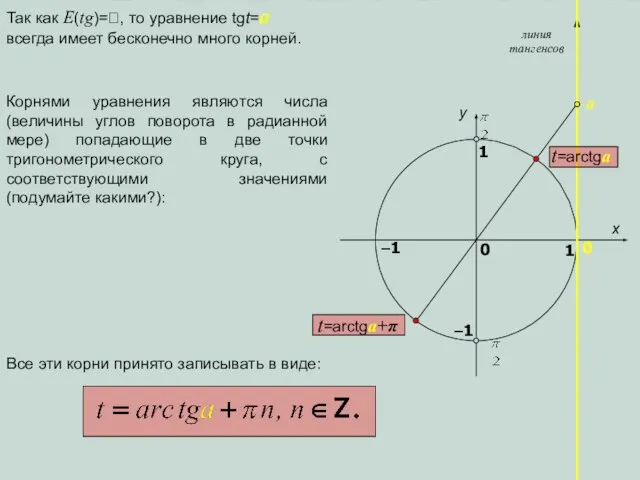
x
y
1
0
1
–1
0
линия тангенсов
a
Так как E(tg)=, то уравнение tgt=a всегда имеет бесконечно много корней.
–1
Корнями уравнения являются числа (величины углов поворота в радианной мере) попадающие в две точки тригонометрического круга, с соответствующими значениями (подумайте какими?):
Все эти корни принято записывать в виде: