Содержание
- 2. Разработать математическую модель, позволяющую описать полет баскетбольного мяча, брошенного игроком в баскетбольную корзину. Модель должна позволять:
- 3. Концептуальная постановка задачи Гипотезы: объектом моделирования является баскетбольный мяч радиуса R; мяч будем считать материальной точкой
- 4. Математическая постановка: В проекциях на оси координат: Точность броска: Δ = x(tk) – xk, где tk
- 5. Рис. Схема к оценке точности броска
- 6. Эффект Магнуса «Крученый мяч» Возникновение поперечной силы, действующей на тело, вращающееся в набегающем на него потоке
- 7. Если вращающийся шар обтекает безвихревой поток, то вследствие вязкости жидкости скорость течения со стороны, где направления
- 8. Требуется найти функцию y(t), удовлетворяющую дифференциальному уравнению где f(t, y(t)) – заданная непрерывная функцию двух аргументов.
- 9. Метод Эйлера Заменим производную функции в точке разностным аналогом: Тогда дифференциальное уравнение можно заменить разностным: Окончательно
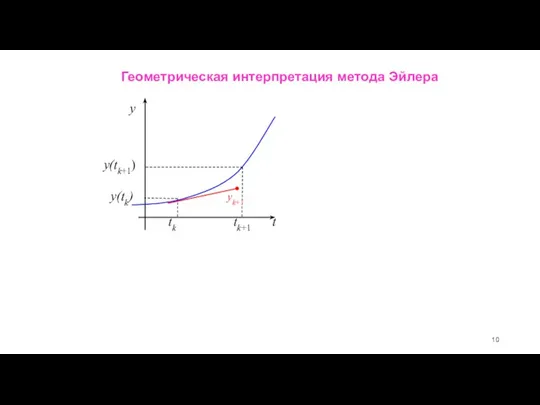
- 10. Геометрическая интерпретация метода Эйлера
- 11. Математическая постановка задачи движения мяча с учетом эффекта Магнуса: Уравнение движения в векторном виде: Начальные условия:
- 12. Уравнения движения в проекциях на оси: Начальные условия:
- 13. Чтобы записать расчетную схему метода Эйлера, каждое дифференциальное уравнение второго порядка заменим двумя уравнениями первого порядка:
- 14. Тогда схема метода Эйлера:
- 16. Скачать презентацию












 Теорема Пифагора
Теорема Пифагора Классы интегрируемых функций
Классы интегрируемых функций Интеллектуальная игра по математике для 8 класса
Интеллектуальная игра по математике для 8 класса Движение в геометрии
Движение в геометрии Математическая модель
Математическая модель Примеры. Карточки, счет +-10, 11, 12
Примеры. Карточки, счет +-10, 11, 12 Анализ уравнения на соответствие графику
Анализ уравнения на соответствие графику Масса предметов
Масса предметов Теория игр
Теория игр Методика изучения площади
Методика изучения площади Элементы комбинаторики. Перестановки
Элементы комбинаторики. Перестановки Линейная зависимость и линейная независимость системы векторов. Семинар 4
Линейная зависимость и линейная независимость системы векторов. Семинар 4 Осевая семетрия
Осевая семетрия Координатная плоскость. Ордината. Абсцисса
Координатная плоскость. Ордината. Абсцисса Алгоритм и письменное деление на двузначное число
Алгоритм и письменное деление на двузначное число Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша)
Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша)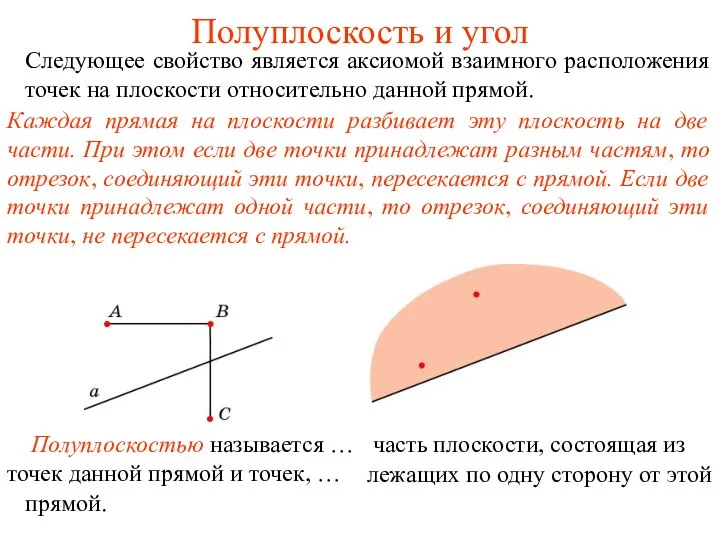 Полуплоскость и угол
Полуплоскость и угол Компланарны ли тройки векторов
Компланарны ли тройки векторов Четырехугольники
Четырехугольники Общее уравнение прямой и плоскости. Лекция1 (1)
Общее уравнение прямой и плоскости. Лекция1 (1) Математика интелектуальная разминка
Математика интелектуальная разминка Усеченый конус
Усеченый конус Кратчайшие расстояния
Кратчайшие расстояния Параллельные прямые 7 класс
Параллельные прямые 7 класс Таблица истинности
Таблица истинности Готфрид Лейбниц (1646 – 1716) – немецкий математик, физик, философ, юрист, языковед
Готфрид Лейбниц (1646 – 1716) – немецкий математик, физик, философ, юрист, языковед Таблицы данных с двумя переменными
Таблицы данных с двумя переменными Показательные уравнения и неравенства
Показательные уравнения и неравенства