- Главная
- Математика
- Каков развивающий потенциал функциональной линии в курсе математики?

Содержание
Слайд 2Одним из центральных понятий школьного курса математики, которое в значительной мере определяет
Одним из центральных понятий школьного курса математики, которое в значительной мере определяет

ее обучающий, воспитывающий и развивающий потенциал, является понятие функции.




 Решение задач на движение в противоположных направлениях
Решение задач на движение в противоположных направлениях Подготовка к к/р
Подготовка к к/р Презентация по математике "Использование информационных технологий в преподавании математики" -
Презентация по математике "Использование информационных технологий в преподавании математики" -  История возникновения процентов
История возникновения процентов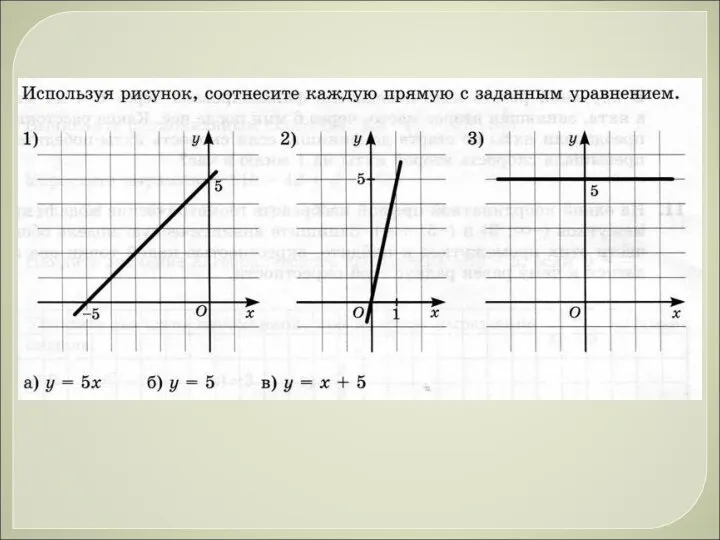 Соотношение прямой с заданным уравнением
Соотношение прямой с заданным уравнением Консультация к экзамену по математике в форме ЕГЭ. Задания В1 - В15
Консультация к экзамену по математике в форме ЕГЭ. Задания В1 - В15 Считаем в уме
Считаем в уме Равнобедренный треугольник
Равнобедренный треугольник Маршрутный лист группы
Маршрутный лист группы Презентация на тему Свойства функции
Презентация на тему Свойства функции  Число потоков в графе
Число потоков в графе Основные типы дифференциальных уравнений первого порядка
Основные типы дифференциальных уравнений первого порядка Транспортир Измерение углов Транспортир. История транспортира. Использование транспортира в жизни человека. Виды транспортир
Транспортир Измерение углов Транспортир. История транспортира. Использование транспортира в жизни человека. Виды транспортир Целые числа. Обзор и контроль
Целые числа. Обзор и контроль Скрещивающиеся прямые. Вопросы, задачи
Скрещивающиеся прямые. Вопросы, задачи Решение задач на дроби
Решение задач на дроби Координатные векторы
Координатные векторы Построение сечений тетраэдра и параллелепипеда
Построение сечений тетраэдра и параллелепипеда Математика. Основные понятия математики
Математика. Основные понятия математики Динамика системы вблизи цикла
Динамика системы вблизи цикла Правильные многогранники в представлении пяти стихий
Правильные многогранники в представлении пяти стихий Кривые второго порядка
Кривые второго порядка Разложение многочлена на множители. Работа над ошибками
Разложение многочлена на множители. Работа над ошибками Преобразование логарифмических выражений
Преобразование логарифмических выражений Квадратные уравнения
Квадратные уравнения Путешествие по родному краю. Курильский заповедник. Выбери наибольшее число
Путешествие по родному краю. Курильский заповедник. Выбери наибольшее число Второй признак равенства треугольников
Второй признак равенства треугольников Многогранники. Призма
Многогранники. Призма