Слайд 2ГЕОМЕТРИЧЕСКОЕ ПОСТРОЕНИЕ
Графический способ решения
геометрических задач на плоскости
при помощи чертежных
инструментов

Слайд 3ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
Деление отрезка на равные части;
Деление угла на равные части;
Нахождение центра

дуги;
Деление окружностей на равные части;
Орнамент
Слайд 4ДЕЛЕНИЕ ОТРЕЗКА на равные части
Дан отрезок АВ, который нужно поделить на

две равные части.
Слайд 5Из концов отрезка А и В циркулем проводят две дуги окружности радиусом

R, несколько большим половины отрезка, до взаимного пересечения в точках а и в.
Слайд 6Через полученные точки а и в проведем прямую, которая пересекает отрезок АВ

в точке С, делящей отрезок на две равные части.
Слайд 7ДЕЛЕНИЕ ОТРЕЗКА на две и четыре равные части
Проделав подобные построения для

отрезков АС и СВ, получим точки D и F. Точки С, D и F делят отрезок АВ на четыре равные части.
Слайд 8ДЕЛЕНИЕ ОТРЕЗКА на равные части
А
В
С
•
•
•
•
1
2
4
3
2'
1'
3'
4'
Теорема Фалеса
Если на одной стороне угла отложить
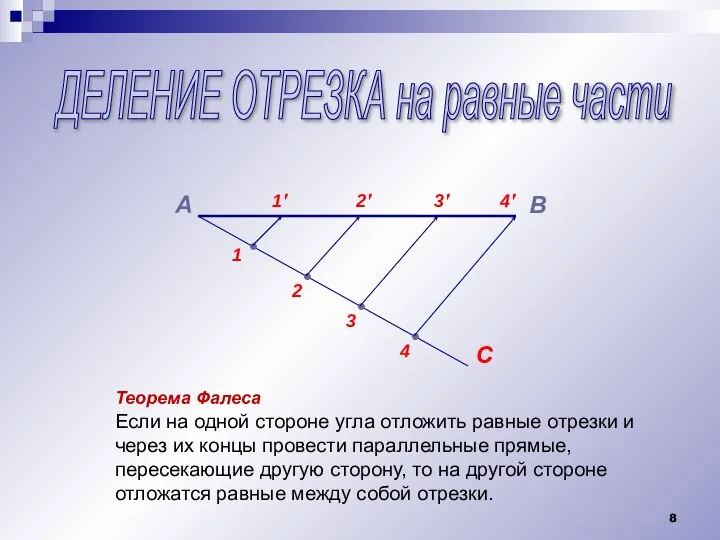
равные отрезки и через их концы провести параллельные прямые, пересекающие другую сторону, то на другой стороне отложатся равные между собой отрезки.
Слайд 9ДЕЛЕНИЕ УГЛА на равные части
Дан угол АВС, который необходимо разделить на

две равные части.
Для того чтобы разделить угол АВС пополам нужно провести биссектрису из вершины угла.
Слайд 10Построение биссектрисы выполняется в следующей последовательности:
Из вершины угла проводят дугу окружности произвольного

радиуса r до пересечения со сторонами угла в точках D и F;
Слайд 11Из полученных точек проводят две дуги радиусом R, величина которого больше половины

длины дуги DF, до взаимного пересечения в точке К;
Прямая проходящая через вершину В и точку К - биссектриса данного угла т.е. делит угол на две равные части.
Слайд 12ДЕЛЕНИЕ УГЛА на равные части
Дан угол АВС, который необходимо разделить на

три равные части.
Слайд 13Деление прямого угла АВС на три равные части выполняется в следующей последовательности:
Из

вершины угла проводят дугу окружности произвольного радиуса R до пересечения со сторонами угла в точках D и F;
Слайд 14Из полученных точек проводят две дуги тем же радиусом R, до взаимного

пересечения с дугой DF в точках К и М;
Точки К и М соединяют с вершиной А прямыми, которые разделят угол АВС на три равные части.
Слайд 15НАХОЖДЕНИЕ ЦЕНТРА ДУГИ
Дана дуга окружности. Необходимо найти центр и радиус окружности

.
Слайд 16Нахождение положения центра и величины радиуса данной дуги окружности выполняется в следующей

последовательности:
1. На дуге произвольно выбирают три точки A, В и С;
Слайд 172. Соединяют выбранные точки отрезками (хордами);
К отрезкам АВ и ВС через их

середины восстанавливают перпендикуляры;
Слайд 18К отрезкам АВ и ВС через их середины восстанавливают перпендикуляры;

Слайд 193. Точка О пересечения перпендикуляров определяет положение центра дуги, а отрезок ОА

равен радиусу дуги.
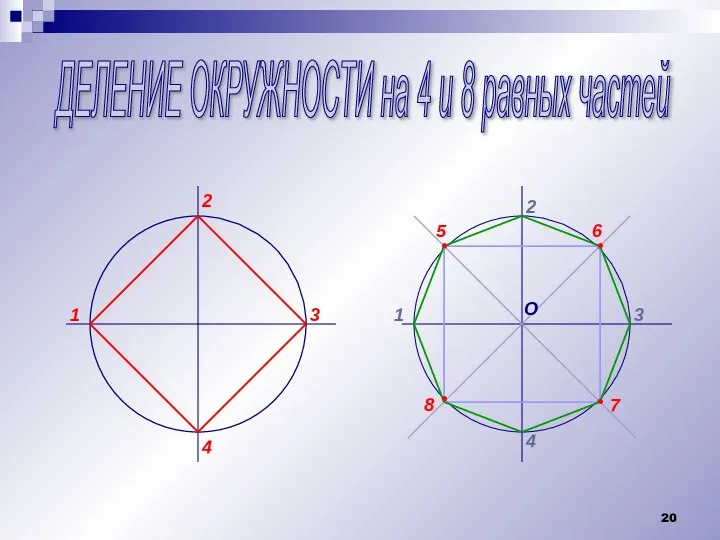
Слайд 20ДЕЛЕНИЕ ОКРУЖНОСТИ на 4 и 8 равных частей
1
2
3
4
5
1
2
3
4
6
7
8
•
•
•
•
О
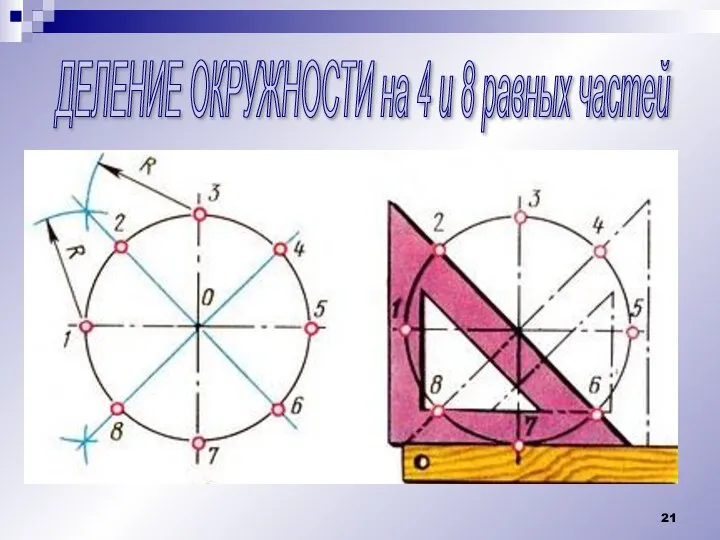
Слайд 21ДЕЛЕНИЕ ОКРУЖНОСТИ на 4 и 8 равных частей
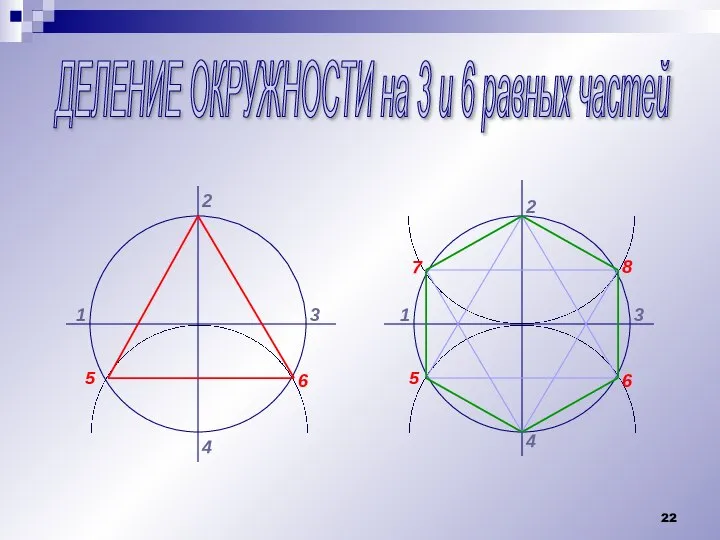
Слайд 22ДЕЛЕНИЕ ОКРУЖНОСТИ на 3 и 6 равных частей
1
2
3
4
5
6
1
3
2
4
5
6
7
8
Слайд 23ДЕЛЕНИЕ ОКРУЖНОСТИ на 3 равных частей
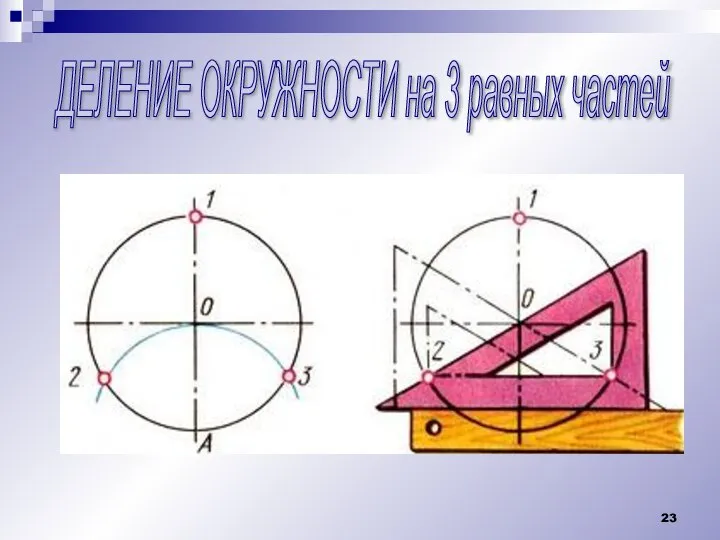
Слайд 24ДЕЛЕНИЕ ОКРУЖНОСТИ на 6 равных частей
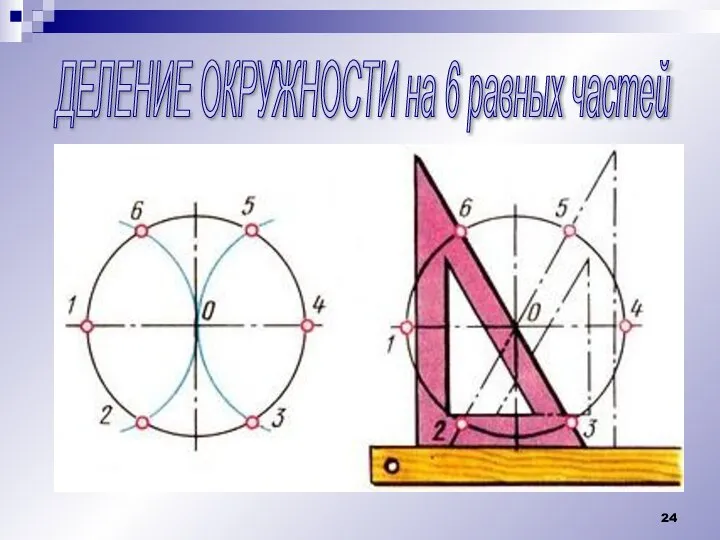
Слайд 25ДЕЛЕНИЕ ОКРУЖНОСТИ на 6 и 12 равных частей
1
2
3
4
а
с
в
d
5
6
7
8
•
•
•
•
•
•
•
•
9
10
11
12

Слайд 26ДЕЛЕНИЕ ОКРУЖНОСТИ на 12 равных частей

Слайд 27ДЕЛЕНИЕ ОКРУЖНОСТИ на 5 равных частей
•
A
O
B
C
R
C = ½[OB]
R = [AC]
•
•
4
5
2
3
•
•
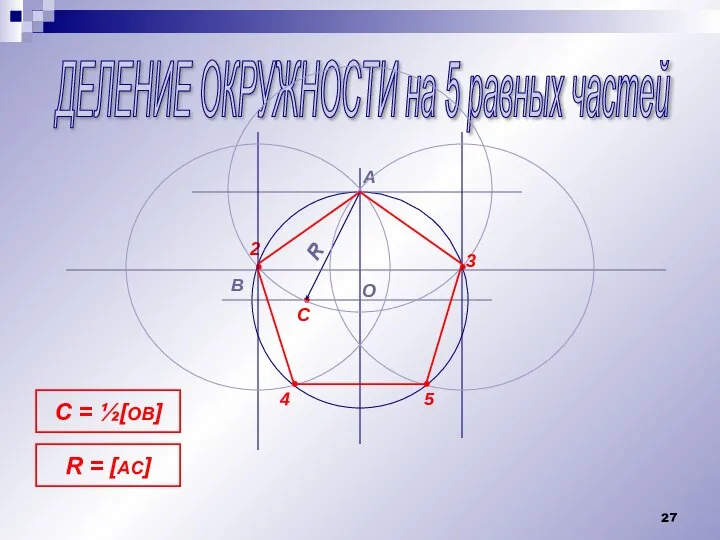
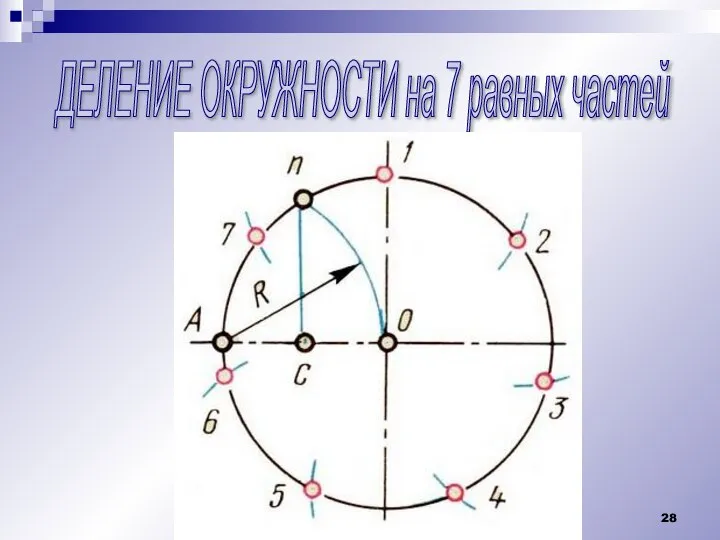
Слайд 28ДЕЛЕНИЕ ОКРУЖНОСТИ на 7 равных частей



























 Тригонометрические уравнения и методы их решений
Тригонометрические уравнения и методы их решений Решение тригонометрических уравнений
Решение тригонометрических уравнений Основы логики
Основы логики Последовательности. Предел последовательности. Отображение
Последовательности. Предел последовательности. Отображение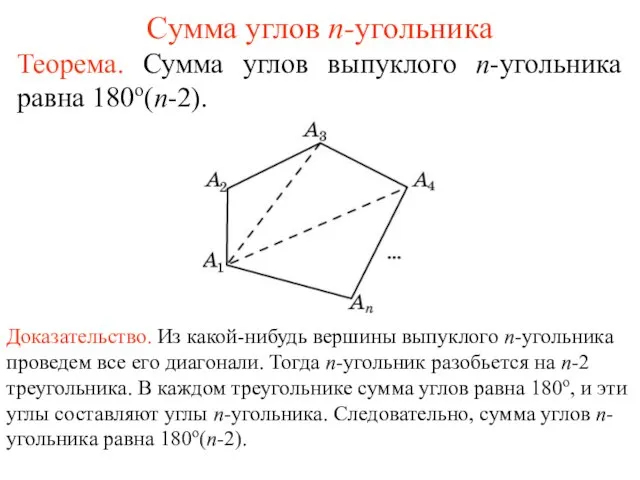 Презентация на тему Сумма углов n-угольника
Презентация на тему Сумма углов n-угольника  Презентация на тему Деление и дроби (5 класс)
Презентация на тему Деление и дроби (5 класс)  Делимость целых чисел
Делимость целых чисел Третий признак равенства треугольников. Математический диктант
Третий признак равенства треугольников. Математический диктант Треугольники и их виды
Треугольники и их виды Презентация на тему Теорема Пифагора и её применение
Презентация на тему Теорема Пифагора и её применение 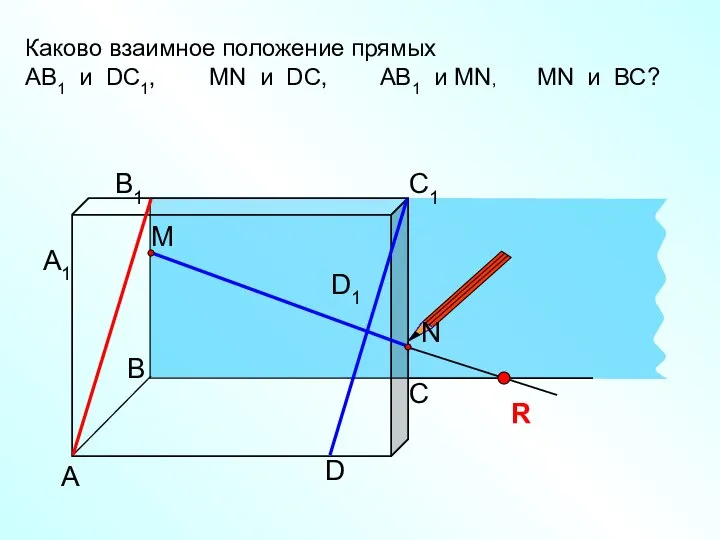 параллельность прямых и плоскостей 10
параллельность прямых и плоскостей 10 Тела и поверхности вращения
Тела и поверхности вращения Аксиомы
Аксиомы Понятие доли
Понятие доли Показательная функция. Построение и преобразование графика функции
Показательная функция. Построение и преобразование графика функции Презентация на тему Геометрические тела
Презентация на тему Геометрические тела  Развертка. Создание объёмных фигур из плоскости
Развертка. Создание объёмных фигур из плоскости Алгебраический способ решения задач (часть 1)
Алгебраический способ решения задач (часть 1) Матрицы и определители
Матрицы и определители Презентация на тему Отношения (6 класс)
Презентация на тему Отношения (6 класс)  Как построить графики функций y = f(x) + b и y = f(x + a), если известен график функции y = f(x)
Как построить графики функций y = f(x) + b и y = f(x + a), если известен график функции y = f(x) Признаки равнобедренного треугольника
Признаки равнобедренного треугольника Своя игра. Треугольники
Своя игра. Треугольники Сфера и шар
Сфера и шар Касательная к окружности. Решение задач
Касательная к окружности. Решение задач Элементы комбинаторики. Лекция 111
Элементы комбинаторики. Лекция 111 Движения
Движения Построение графика функции
Построение графика функции