Конструктивная геометрия. Решение задач способом замены плоскостей проекции

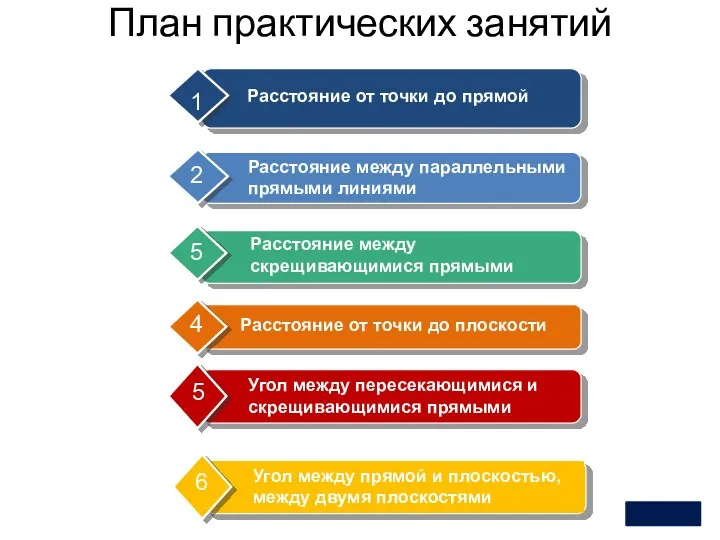
План практических занятий
1

Вступление
В предыдущей лекции отмечено, что метрические задачи - это задачи связанные с измерением, а именно,на определение натуральной величины размеров заданных фигур: расстояний (длин), углов, контуров плоских геометрических форм
2

Из свойств ортогонального проецирования отметили, если прямая параллельна плоскости проекций (прямая уровня), то её отрезок на эту плоскость проекций изображается в натуральную величину.
Аналогичное свойство имеет плоская фигура, расположенная в плоскости уровня.
Таким образом, результат решения задачи имеет место, когда прямая и плоскость занимают частное положение относительно плоскостей проекций
2
Вступление

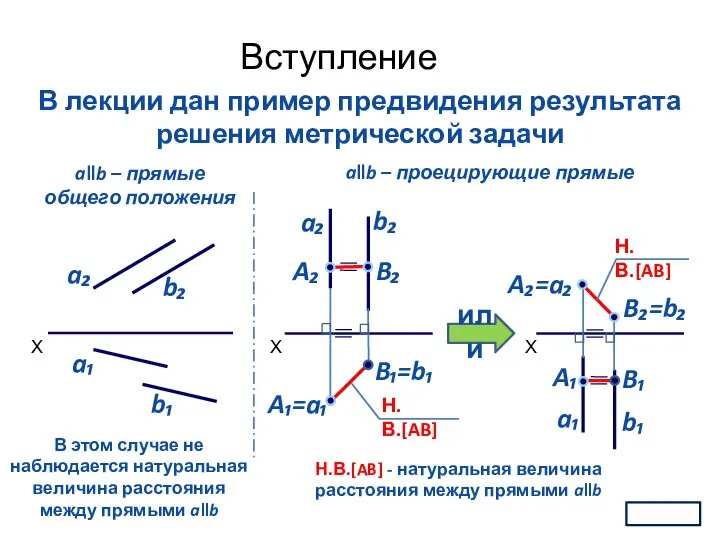
В лекции дан пример предвидения результата решения метрической задачи
X
a₁
b₁
a₂
b₂
X
A₂
B₂
A₁=a₁
B₁=b₁
a₂
b₂
X
A₂=a₂
B₂=b₂
A₁
B₁
a₁
b₁
aǁb – прямые общего положения
aǁb – проецирующие прямые
Н.В.[AB]
Н.В.[AB]
В этом случае не наблюдается натуральная величина расстояния между прямыми aǁb
Н.В.[AB] - натуральная величина расстояния между прямыми aǁb
Вступление

Вступление
2
Отмечено положение: решение метрических задач значительно облегчается, когда заданные геометрические объекты занимают частные положения, т.е. параллельны и/или перпендикулярны относительно плоскостей проекций. В связи с этим, во многих решаемых задачах возникает необходимость преобразования комплексного чертежа, при котором заданные геометрические объекты переводятся из общего положения в частное

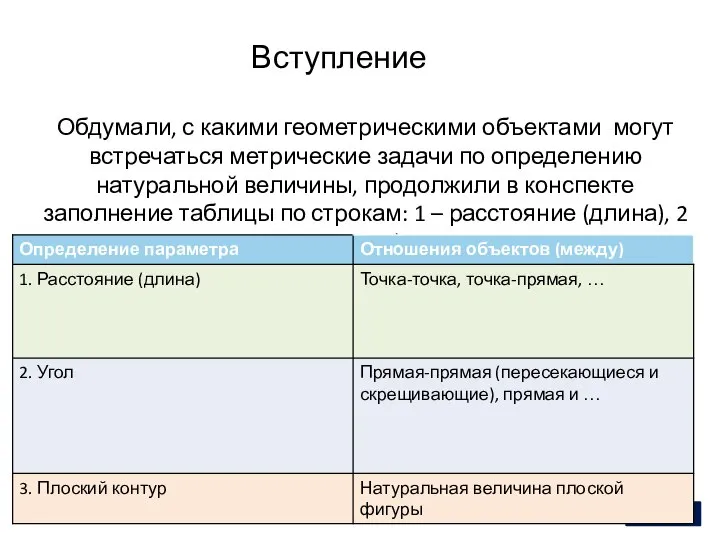
Вступление
2
Обдумали, с какими геометрическими объектами могут встречаться метрические задачи по определению натуральной величины, продолжили в конспекте заполнение таблицы по строкам: 1 – расстояние (длина), 2 – угол)

Вступление
2
В лекции отмечено, что метрические задачи, решаются посредством определенного способа преобразования на основе реализации четырех основных задач :
1) преобразование прямой общего положения в прямую уровня;
2) преобразование прямой уровня в прямую проецирующую;
3) преобразование плоскости общего положения в плоскость проецирующую;
4) преобразование проецирующей плоскости в плоскость уровня.
Необходимо запомнить формулировку четырех основных задач

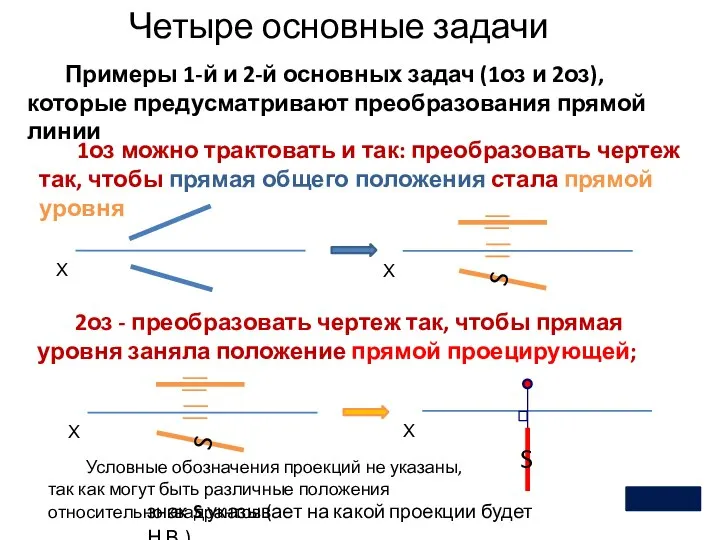
Четыре основные задачи
2
Примеры 1-й и 2-й основных задач (1оз и 2оз), которые предусматривают преобразования прямой линии
1оз можно трактовать и так: преобразовать чертеж так, чтобы прямая общего положения стала прямой уровня
2оз - преобразовать чертеж так, чтобы прямая уровня заняла положение прямой проецирующей;
X
X
X
X
Условные обозначения проекций не указаны, так как могут быть различные положения относительно квадрантов (
S
S
S
знак S указывает на какой проекции будет Н.В.)

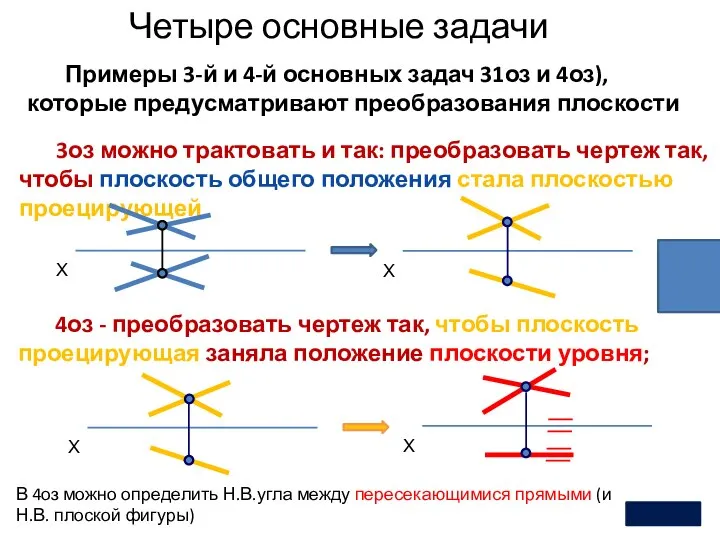
Четыре основные задачи
2
Примеры 3-й и 4-й основных задач 31оз и 4оз), которые предусматривают преобразования плоскости
3оз можно трактовать и так: преобразовать чертеж так, чтобы плоскость общего положения стала плоскостью проецирующей
4оз - преобразовать чертеж так, чтобы плоскость проецирующая заняла положение плоскости уровня;
X
X
X
X
В 4оз можно определить Н.В.угла между пересекающимися прямыми (и Н.В. плоской фигуры)

Метрические задачи.
Основные положения (три важных аспекта)
2
Таким образом, рассмотрим три очень важных аспекта, без знаний которых требуемую метрическую задачу не решить:
1 аспект – необходимо предвидеть конечный результат решаемой задачи (казалось бы мы не знаем как ещё решать, но в соответствии с представленными выше примерами, их необходимо обобщить на остальные задачи в составленной Вами таблице (решаемые задачи);
2 аспект – для решения конкретной задачи необходимо освоить четыре основные задачи, как «подзадачи», применение которых позволит выполнить решение конкретной задачи. При этом, возможно нужно будет применить только одну основную задачу, или последовательно за ней и следующую;
3 аспект – поставленная задача решается одним из способов преобразования комплексного чертежа (т.е. ортогональных проекций). В конструктивной (начертательной) геометрии таких способов несколько, поэтому следующие слайды посвящены способам преобразования и решению основных задач с примерами.

Метрические задачи.
Основные положения (способы преобразования)
2
В соответствии с решением метрических задач можно подразделить такие способы преобразования, при которых геометрический объект(ы), при решении поставленной задачи, остаются фиксированными (неизменными) относительно системы плоскостей проекций, в другом преобразовании – геометрические объекты меняют своё положение относительно плоскостей проекций.
Любой из этих способов преобразования однозначно приводит к решению поставленной задачи, при условии, что Вами, во-первых, в общем виде реализуется предвиденье результата решения задачи, это – выполнение первого аспекта, во-вторых, Вы обоснованно применили реализацию основной(ных) задач – это второй аспект.
В результате этих преобразований будет получен чертёж, облегчающий дальнейшее решение задачи, либо на выполняемом чертеже будет получено готовое решение задачи.

Из лекции известно, что способ замены плоскостей проекций заключается в замене одной из плоскостей проекций на другую (новую) плоскость проекций, на которой задача решается проще или будет получен готовый результат решения.
Геометрическая фигура относительно исходной системы плоскостей проекций П₁, П₂, П₃ своего положения не меняет!
Способ замены плоскостей проекций
При этом должны быть обязательно выдержаны два условия:
1. Новая плоскость проекций по отношению к оставшейся плоскости проекций должна быть перпендикулярна (но таких новых плоскостей может быть множество, тогда необходимо второе условие:
2. Новая плоскость проекций ориентируется в соответствии с применяемой основной задачи
3

͡
͡
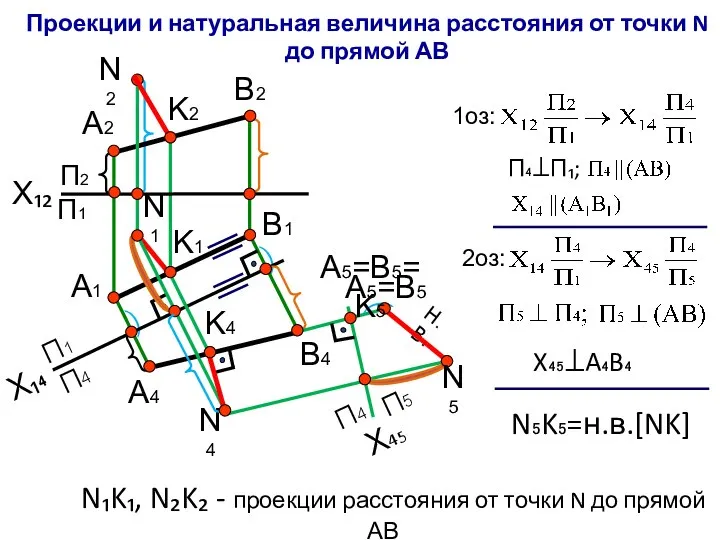
Проекции и натуральная величина расстояния от точки N до прямой АВ
X₁₂
П2
Х₁₄
П1
П4
А1
А2
В4
В1
В2
А4
П1
Н.В.
7
X₄₅⟘A₄B₄
N₅K₅=н.в.[NK]
N₁K₁, N₂K₂ - проекции расстояния от точки N до прямой АВ
͡
K2
K1
K4
A5=B5=K5
N5
Х45
П4
П5
N2
N1
N4
П₄⟘П₁;
1оз:
2оз:
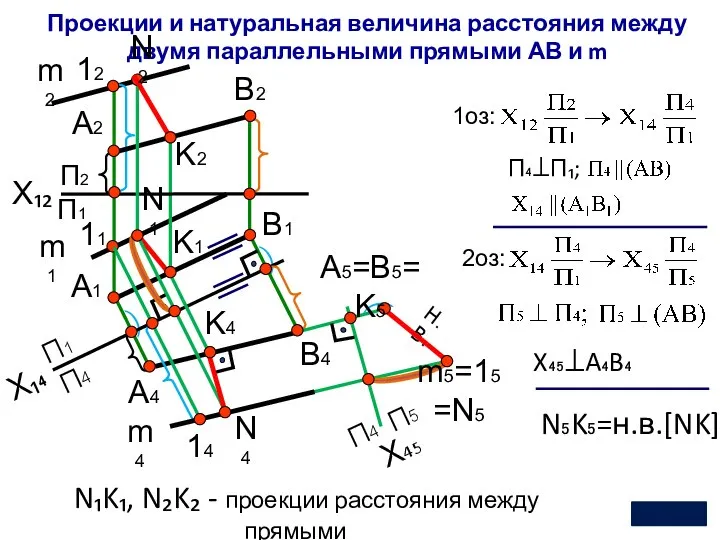
A5=B5

Проекции и натуральная величина расстояния между двумя параллельными прямыми АВ и m
N₅K₅=н.в.[NK]
͡
͡
X₁₂
П2
Х₁₄
П1
П4
А1
А2
В4
В1
В2
А4
П1
Н.В.
7
X₄₅⟘A₄B₄
N₁K₁, N₂K₂ - проекции расстояния между прямыми
͡
m2
K1
K4
A5=B5=K5
m5=15=N5
Х45
П4
П5
N2
N1
N4
П₄⟘П₁;
1оз:
2оз:
12
11
m1
m4
K2
14

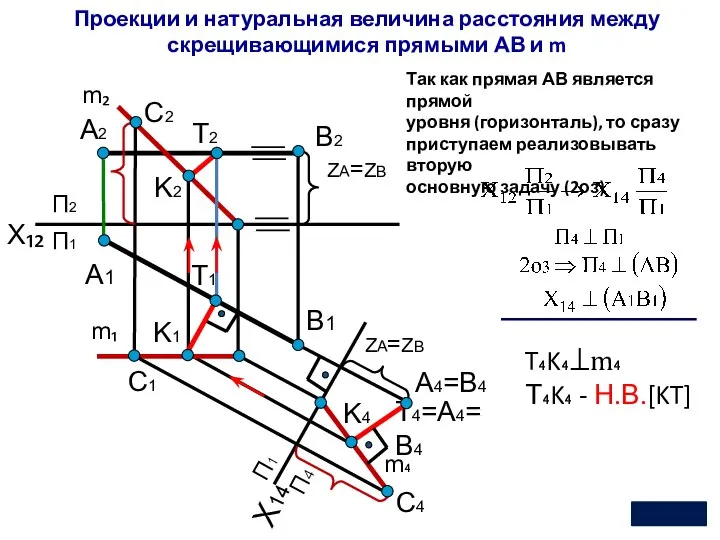
X₁₂
П2
Х14
П1
П4
А1
А2
T4=А4=В4
В1
В2
П1
ZА=ZВ
ZА=ZВ
9
Проекции и натуральная величина расстояния между скрещивающимися прямыми АВ и m
m₂
m₁
m₄
C4
C1
C2
K4
K1
K2
T2
T1
Так как прямая АВ является прямой
уровня (горизонталь), то сразу
приступаем реализовывать вторую
основную задачу (2оз)
T₄K₄⟘m₄
T₄K₄ - Н.В.[KT]
А4=В4

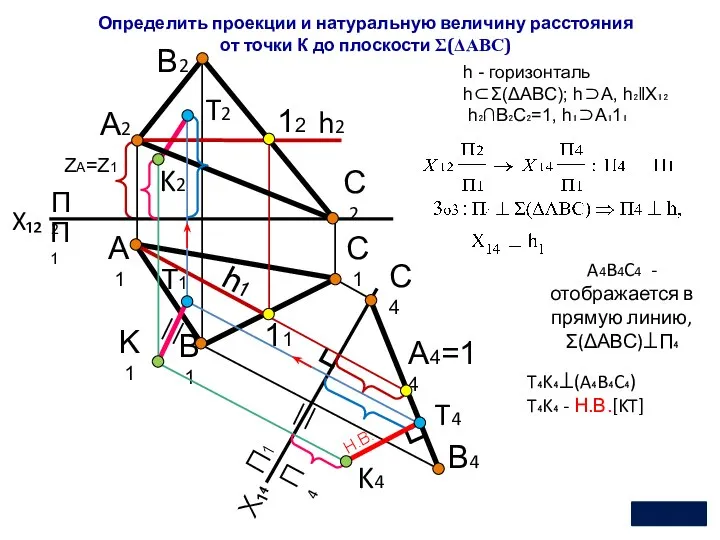
П2
П1
П4
А4=14
П1
ZА=Z1
Н.В.
X₁₂
А2
В2
А1
В1
С2
С1
12
11
h - горизонталь
h⊂Σ(ΔABC); h⊃A, h₂ǁX₁₂
h₂∩B₂C₂=1, h₁⊃A₁1₁
A4B4C4 - отображается в прямую линию,
Σ(ΔАВС)⟘П₄
В4
С4
Определить проекции и натуральную величину расстояния
от точки К до плоскости Σ(ΔАВС)
Х₁₄
13
h2
h1
K1
K2
T1
K4
T4
T2
T₄K₄⟘(A₄B₄C₄)
T₄K₄ - Н.В.[KT]

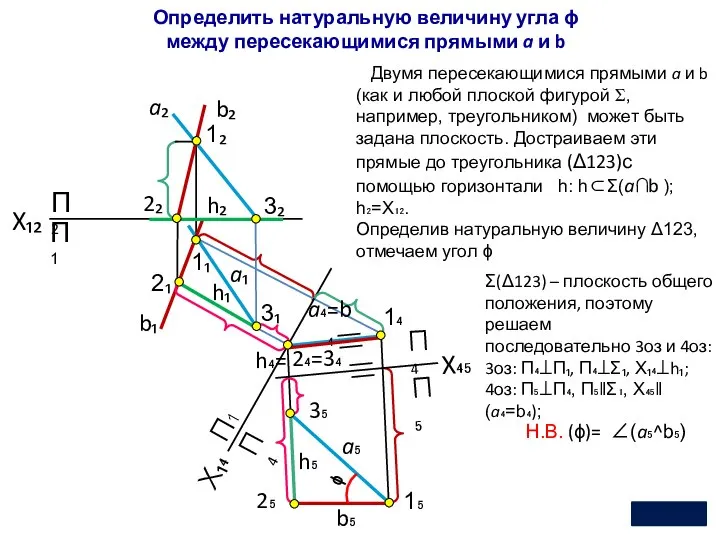
2₄=3₄
П2
П1
П4
П1
X₁₂
Двумя пересекающимися прямыми a и b (как и любой плоской фигурой Σ, например, треугольником) может быть задана плоскость. Достраиваем эти прямые до треугольника (Δ123)с помощью горизонтали h: h⊂Σ(a∩b ); h₂=X₁₂.
Определив натуральную величину Δ123, отмечаем угол ϕ
Определить натуральную величину угла ϕ
между пересекающимися прямыми a и b
Х₁₄
13
h₂
Н.В. (ϕ)= ∠(a₅^b₅)
1₂
2₂
3₂
2₁
1₁
3₁
1₄
1₅
2₅
3₅
П4
П₅
X₄₅
h₁
h₄=
a₂
b₂
b₁
a₁
a₄=b₄
a₅
b₅
h₅
ϕ
Σ(Δ123) – плоскость общего
положения, поэтому решаем
последовательно 3оз и 4оз:
3оз: П₄⟘П₁, П₄⟘Σ₁, Х₁₄⟘h₁;
4оз: П₅⟘П₄, П₅ǁΣ₁, Х₄₅ǁ(a₄=b₄);

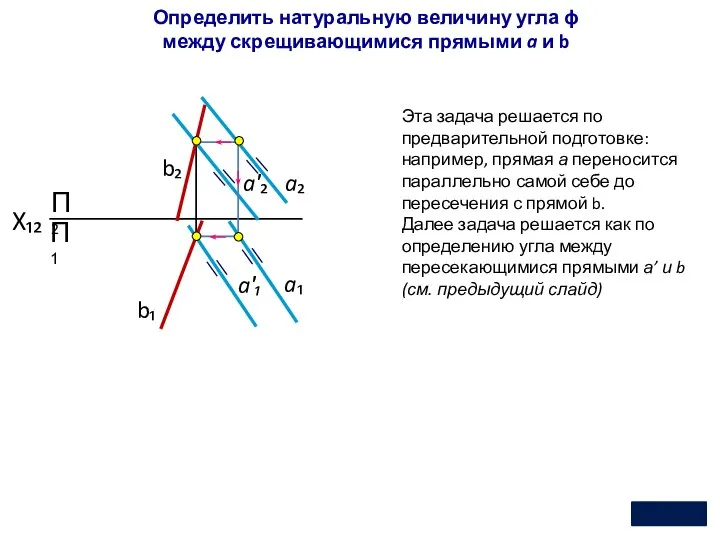
П2
П1
X₁₂
Определить натуральную величину угла ϕ
между скрещивающимися прямыми a и b
a′₂
b₂
b₁
a₁
Эта задача решается по предварительной подготовке:
например, прямая а переносится параллельно самой себе до пересечения с прямой b.
Далее задача решается как по определению угла между пересекающимися прямыми а’ и b (см. предыдущий слайд)
a′₁
a₂

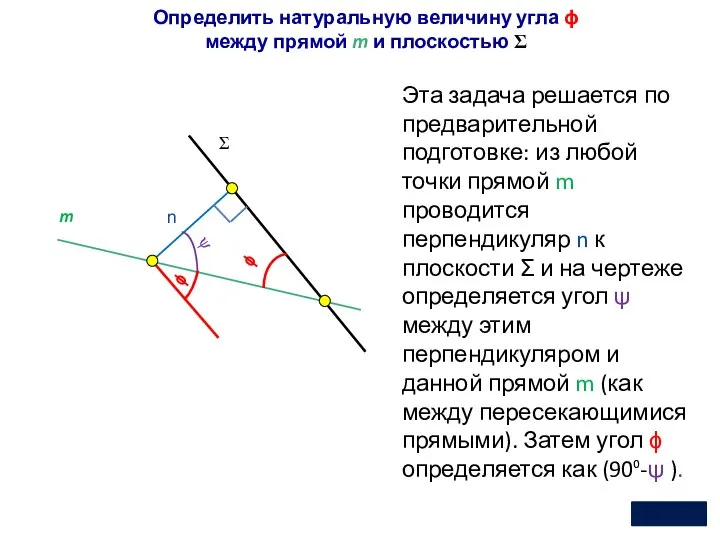
Определить натуральную величину угла ϕ
между прямой m и плоскостью Σ
Эта задача решается по предварительной подготовке: из любой точки прямой m проводится перпендикуляр n к плоскости Σ и на чертеже определяется угол ψ между этим перпендикуляром и данной прямой m (как между пересекающимися прямыми). Затем угол ϕ определяется как (90⁰-ψ ).
Σ
m
n
ψ
ϕ
ϕ