Содержание
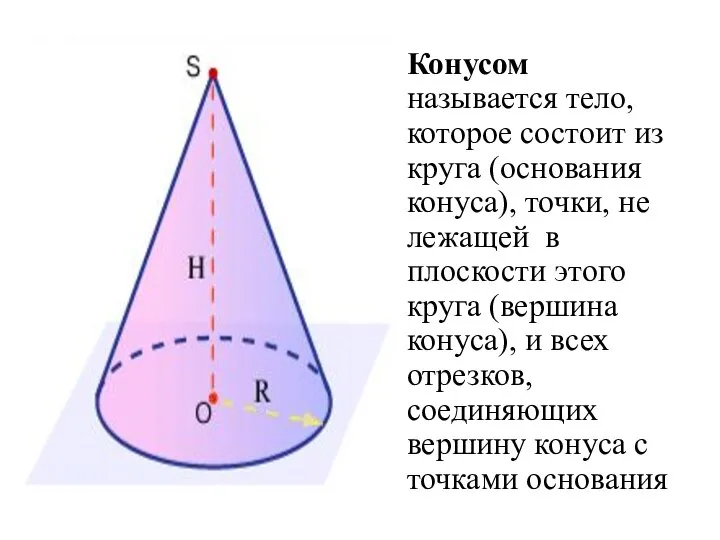
- 2. Конусом называется тело, которое состоит из круга (основания конуса), точки, не лежащей в плоскости этого круга
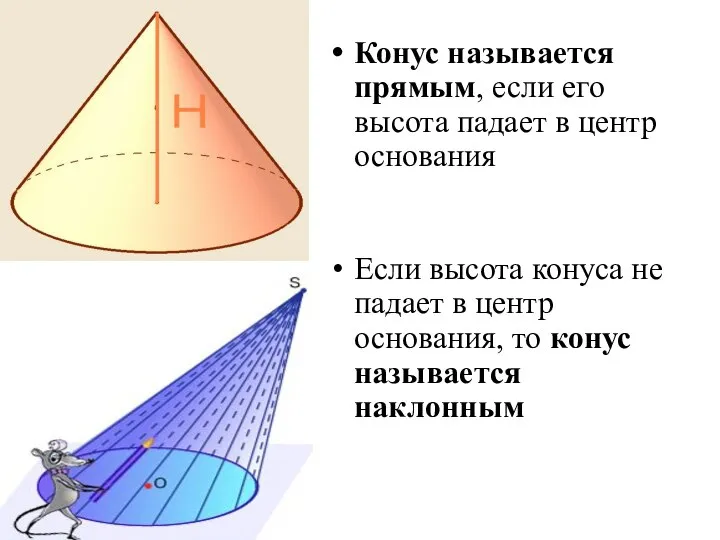
- 3. Конус называется прямым, если его высота падает в центр основания Если высота конуса не падает в
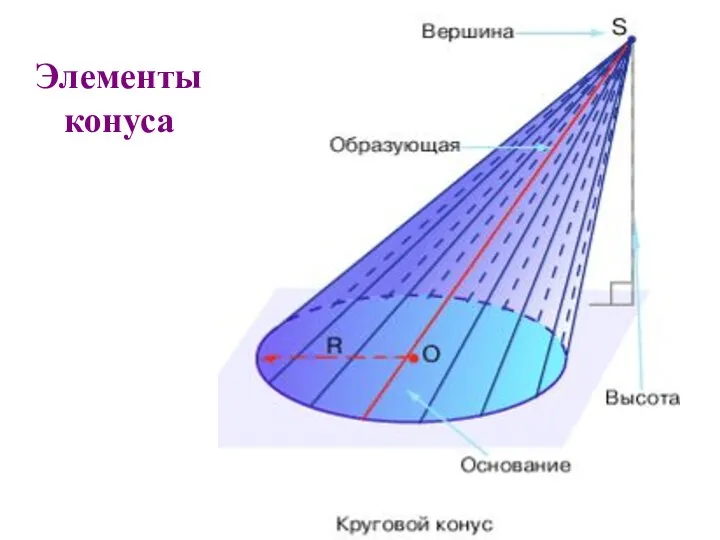
- 4. Элементы конуса
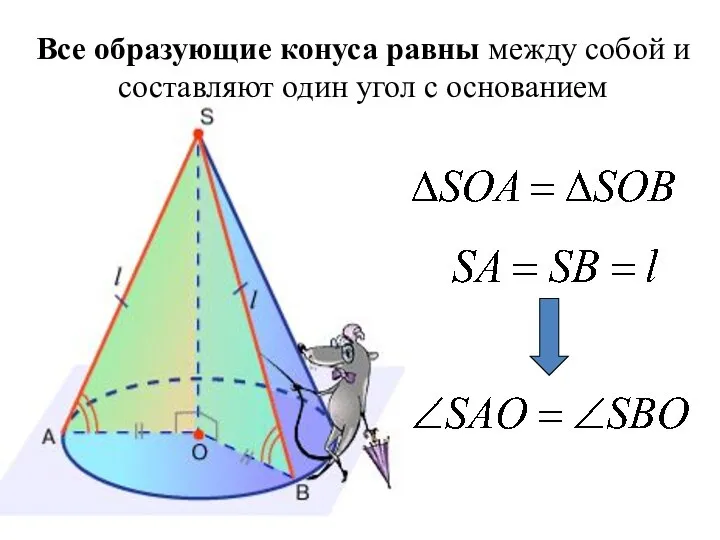
- 5. Все образующие конуса равны между собой и составляют один угол с основанием
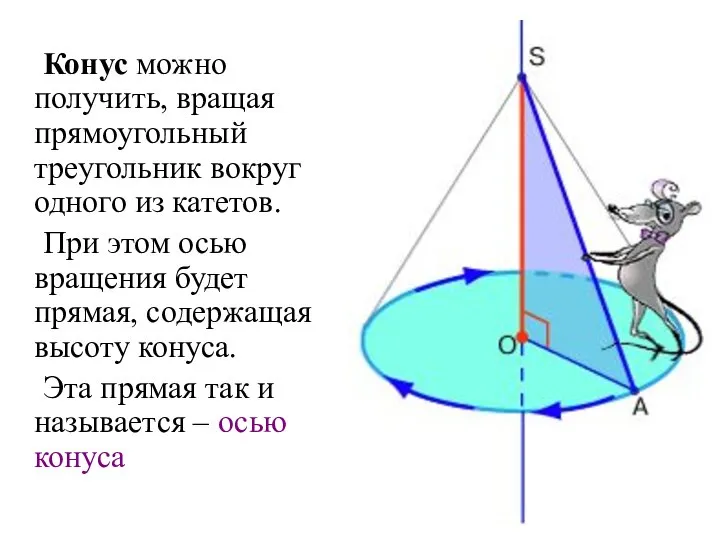
- 6. Конус можно получить, вращая прямоугольный треугольник вокруг одного из катетов. При этом осью вращения будет прямая,
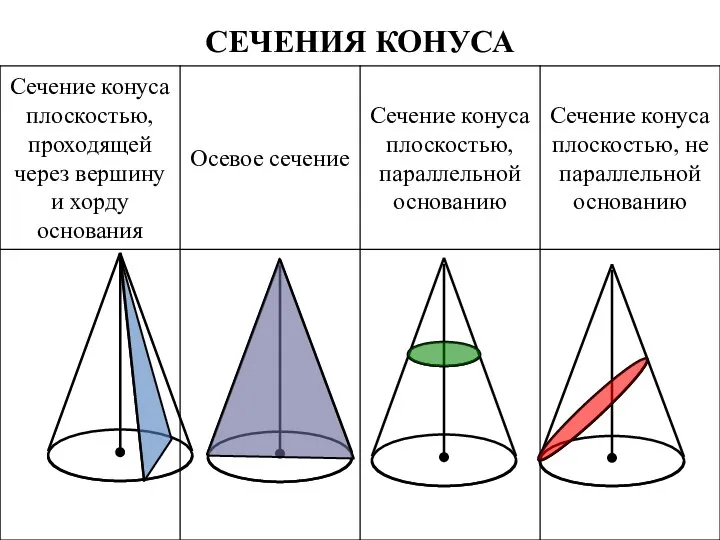
- 7. СЕЧЕНИЯ КОНУСА
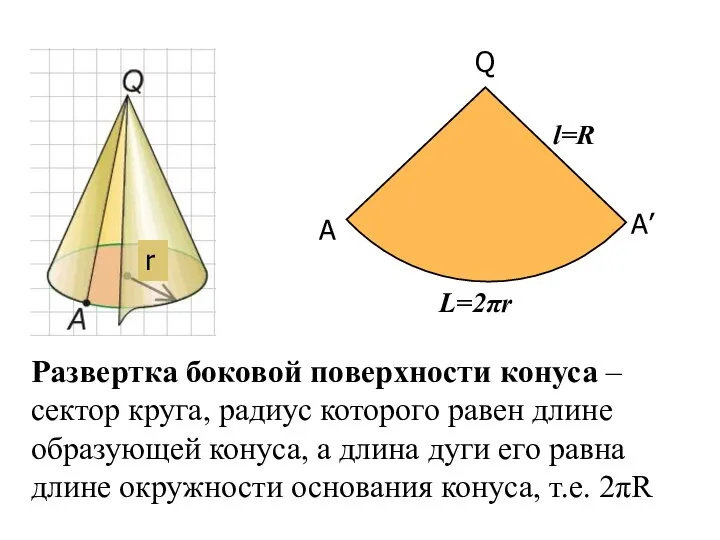
- 8. Развертка боковой поверхности конуса – сектор круга, радиус которого равен длине образующей конуса, а длина дуги
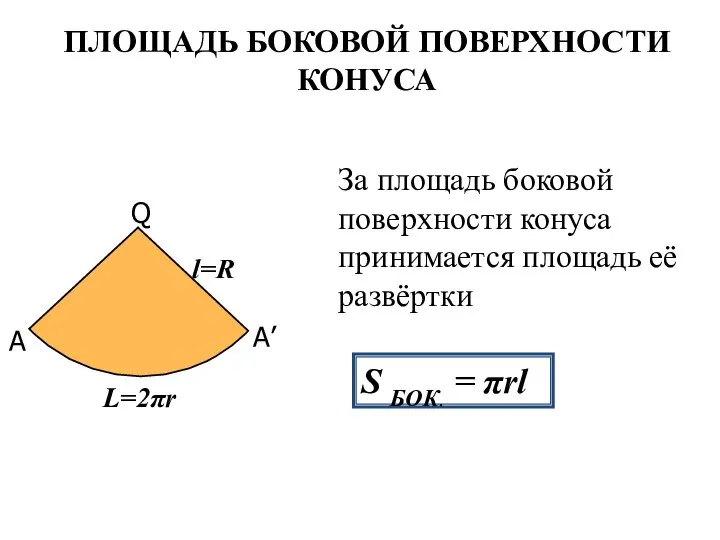
- 9. ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ КОНУСА За площадь боковой поверхности конуса принимается площадь её развёртки S БОК. =
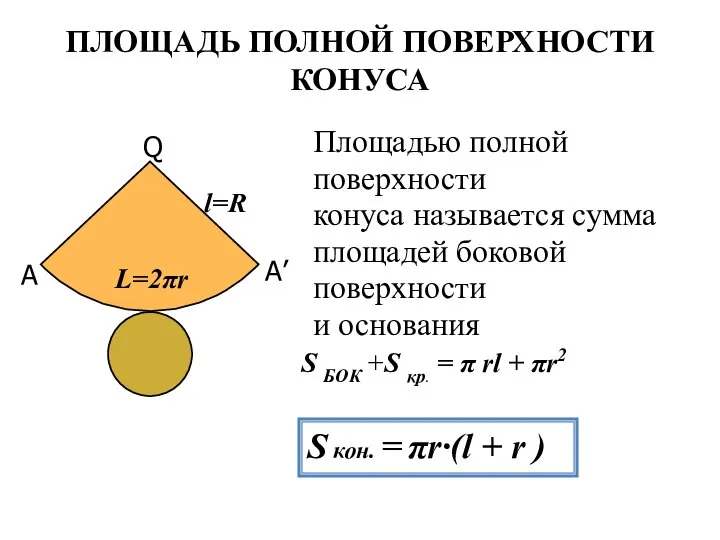
- 10. Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ КОНУСА S
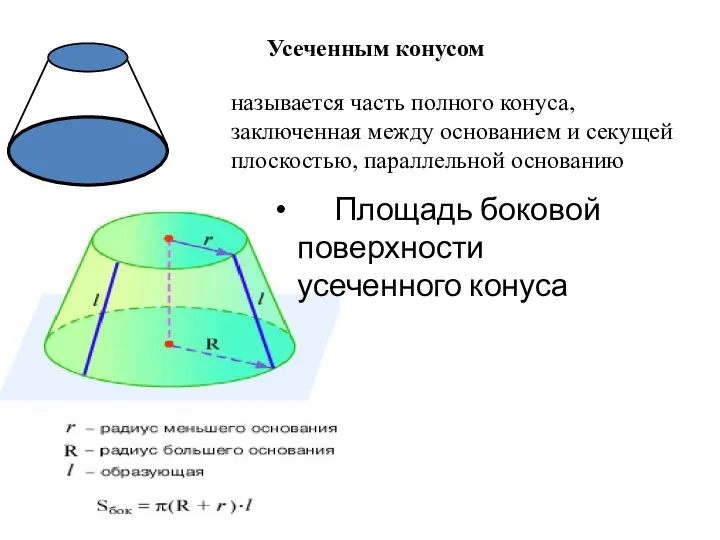
- 11. Усеченным конусом называется часть полного конуса, заключенная между основанием и секущей плоскостью, параллельной основанию Площадь боковой
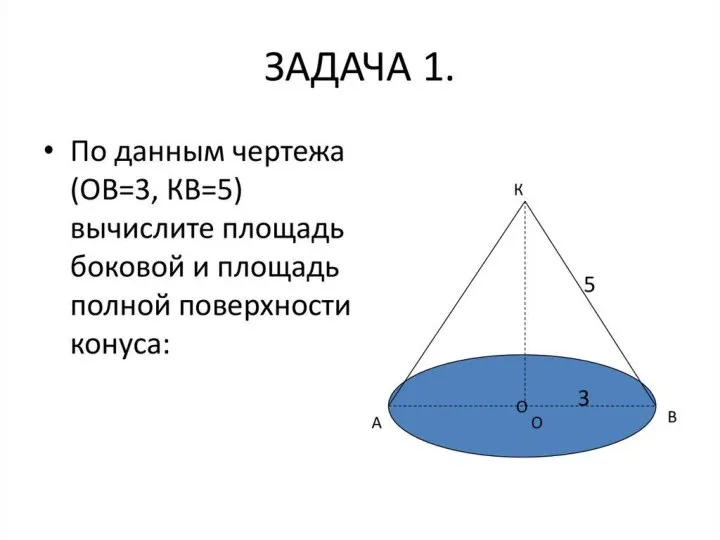
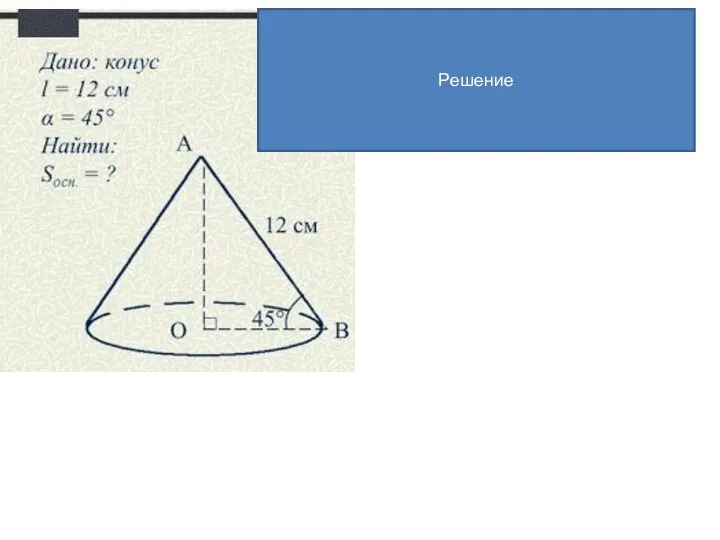
- 13. Решение
- 15. Скачать презентацию
 Презентация на тему Целое и части (1 класс)
Презентация на тему Целое и части (1 класс)  Основное свойство алгебраической дроби
Основное свойство алгебраической дроби Трапеция. Задачи
Трапеция. Задачи Задачи на площадь
Задачи на площадь арифметический корень (1)
арифметический корень (1) Презентация на тему ДЕЛЕНИЕ
Презентация на тему ДЕЛЕНИЕ  Геометрическое решение задачи о расстояниях между точками
Геометрическое решение задачи о расстояниях между точками Умозаключения. Теоремы. Утверждения
Умозаключения. Теоремы. Утверждения Основы анализа данных. Регрессионный анализ. (Лекция 6)
Основы анализа данных. Регрессионный анализ. (Лекция 6) Презентация на тему ГИА 2013. Модуль АЛГЕБРА №7
Презентация на тему ГИА 2013. Модуль АЛГЕБРА №7  Деление и степень числа. Тест
Деление и степень числа. Тест Решение задач по теме треугольники
Решение задач по теме треугольники Признаки параллелограмма
Признаки параллелограмма Уравнения – это ключ, открывающий все математические сезамы. С.Коваль
Уравнения – это ключ, открывающий все математические сезамы. С.Коваль Квадратные уравнения. Урок алгебры в 8 – м классе
Квадратные уравнения. Урок алгебры в 8 – м классе Презентация на тему Игра "О, счастливчик, юный математик"
Презентация на тему Игра "О, счастливчик, юный математик"  Решение логарифмических уравнений
Решение логарифмических уравнений Знаки неравенств. Историческая справка
Знаки неравенств. Историческая справка Тригонометрические формулы суммы и разности углов
Тригонометрические формулы суммы и разности углов Система MatLab/ Методические указания к выполнению лабораторных работ
Система MatLab/ Методические указания к выполнению лабораторных работ Контрольные срезы по математике за 3 четверть - 5,6, 8 класс
Контрольные срезы по математике за 3 четверть - 5,6, 8 класс Векторы в пространстве. Практическая работа
Векторы в пространстве. Практическая работа Повторение и расширение сведений о функции
Повторение и расширение сведений о функции График производной в исследовании функции
График производной в исследовании функции Таблицы сложения и вычитания с числом 2
Таблицы сложения и вычитания с числом 2 Таблица сложения
Таблица сложения Базис векторного пространства
Базис векторного пространства Треугольник. Элементы треугольника
Треугольник. Элементы треугольника