- Главная
- Математика
- Конус прямой круговой

Содержание
Слайд 25.13 б) конус прямой круговой
12
22=22`
42
43
41
11
21
21`
23
13
23`
32=32`
33`
33
31
31`
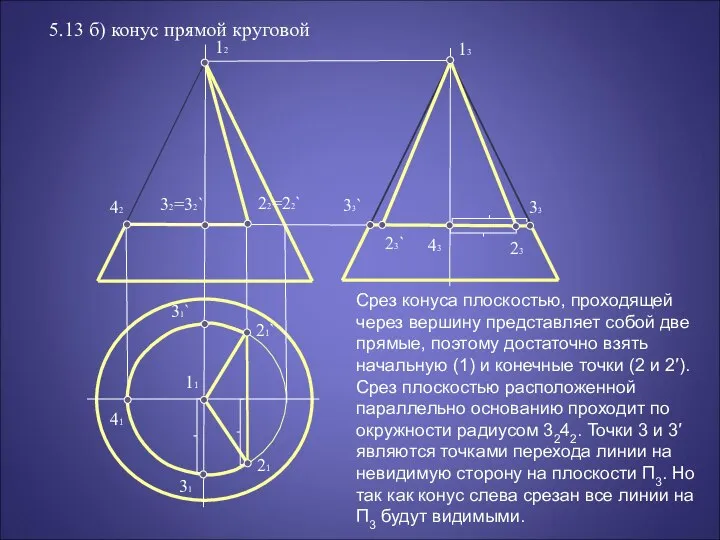
Срез конуса плоскостью, проходящей через вершину представляет собой
5.13 б) конус прямой круговой
12
22=22`
42
43
41
11
21
21`
23
13
23`
32=32`
33`
33
31
31`
Срез конуса плоскостью, проходящей через вершину представляет собой
Слайд 35.13 в) сфера
12
22=22`
32=32`
52=52`
42=42`
62
11
61
41`
51`
31`
21`
33`
43`
23`
53`
63
51
41
31
21
53
43
33
23
13
При пересечении сферы плоскостью общим элементом всегда будет окружность. Если
5.13 в) сфера
12
22=22`
32=32`
52=52`
42=42`
62
11
61
41`
51`
31`
21`
33`
43`
23`
53`
63
51
41
31
21
53
43
33
23
13
При пересечении сферы плоскостью общим элементом всегда будет окружность. Если
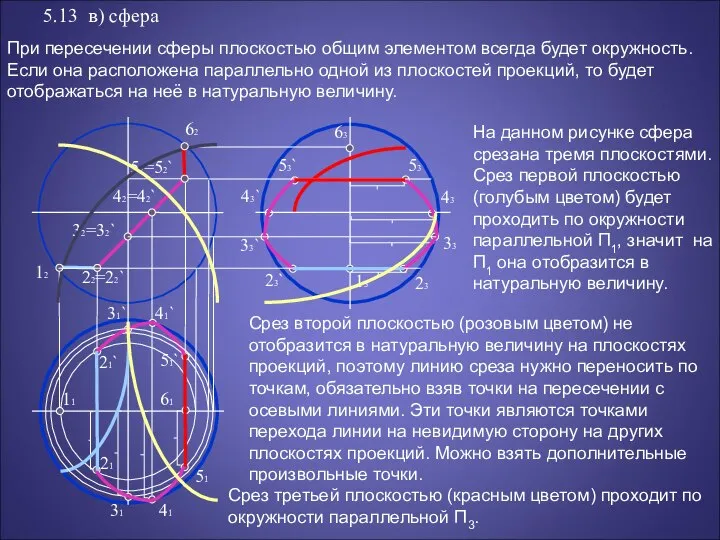
На данном рисунке сфера срезана тремя плоскостями. Срез первой плоскостью (голубым цветом) будет проходить по окружности параллельной П1, значит на П1 она отобразится в натуральную величину.
Срез второй плоскостью (розовым цветом) не отобразится в натуральную величину на плоскостях проекций, поэтому линию среза нужно переносить по точкам, обязательно взяв точки на пересечении с осевыми линиями. Эти точки являются точками перехода линии на невидимую сторону на других плоскостях проекций. Можно взять дополнительные произвольные точки.
Срез третьей плоскостью (красным цветом) проходит по окружности параллельной П3.
 Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Состав числа 7. Головоломка Корова
Состав числа 7. Головоломка Корова Сантиметр - единица измерения длины
Сантиметр - единица измерения длины Числовые последовательности
Числовые последовательности Арифметико-логические устройства. Устройства управления
Арифметико-логические устройства. Устройства управления Площадь произвольного треугольника
Площадь произвольного треугольника Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами
Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами Векторы в пространстве. Практическая работа
Векторы в пространстве. Практическая работа Лишь знанием движется век, Лишь знанием жив человек!
Лишь знанием движется век, Лишь знанием жив человек! Квадратичная функция
Квадратичная функция Меры длины и веса. Задания
Меры длины и веса. Задания Сложение, вычитание многочленов и умножение на одночлен
Сложение, вычитание многочленов и умножение на одночлен Слагаемые. Сумма
Слагаемые. Сумма Подготовка к ЕГЭ 2013. В9. Тема: Нахождение основных элементов цилиндра и конуса
Подготовка к ЕГЭ 2013. В9. Тема: Нахождение основных элементов цилиндра и конуса Презентация на тему Решаем задачи (1 класс)
Презентация на тему Решаем задачи (1 класс)  Интеграл. Что называют криволинейной
Интеграл. Что называют криволинейной Полезная геометрия
Полезная геометрия Экстремум функции двух переменных. Задания
Экстремум функции двух переменных. Задания Методический материал по алгебре
Методический материал по алгебре Тригонометрические уравнения. Найди пару
Тригонометрические уравнения. Найди пару История г. Колпашева в примерах и задачах
История г. Колпашева в примерах и задачах Неравенства (9 класс)
Неравенства (9 класс) урок 1,2 по геометрии 11 класс 6 сентября 2022
урок 1,2 по геометрии 11 класс 6 сентября 2022 Упрощение выражений
Упрощение выражений Применение определенного интеграла при решении геометрических и физических задач
Применение определенного интеграла при решении геометрических и физических задач Вычислите логарифм. Практическая работа
Вычислите логарифм. Практическая работа Связь сложения и умножения
Связь сложения и умножения Глубина озера. Теорема Пифагора
Глубина озера. Теорема Пифагора