Квадратичная функция. Урок алгебры в 8 классе

Расшифруйте слово, выполнив задания
1.
Найти координаты точки,
симметричной точке с координатами
(-2;4),
относительно оси ординат:
Б (4;2) Г (2;4) Д (2;-4)

2.
Найдите значение функции y = x2 , если
x = -2 О y = - 4
П y = 0
P y = 4

3.
Решите уравнение x2 = 4
А -2 и 2 Б - 2 В 2
4.
Решите уравнение x2 = -5
Т -5 У -5 и 5 Ф корней
нет

5.
Какая из точек принадлежит графику
функции y =10 – 5x
И (1;5)
К (5;10)
Л (-1;10)

6.
Какие из функций являются
квадратичными
З y = x3 + 5x + 6
И y = 2x – 6
K y = x2

График квадратичной функции
y = ax2 + bx + c
при a=1,b=c=0

Тема урока 09.04.20г
Функция y = x2 , ее график и свойства
Деятельность – единственный путь
к знанию
Б.Шоу

Функция
Область определения
Аргумент
График функции

Построить график функции y = x2
Математическое исследование
(-3;9)
(-2;4)
(-1;1)
(0;0)
(1;1)
(2;4)
(3;9)
y
x

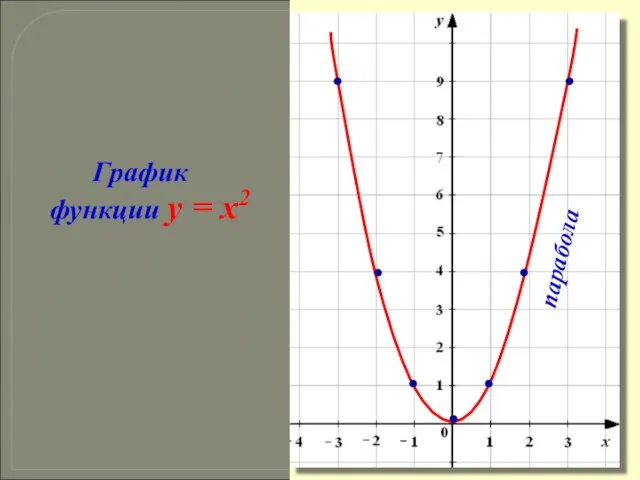
График
функции y = x2
парабола

Свойства функции
y = x2

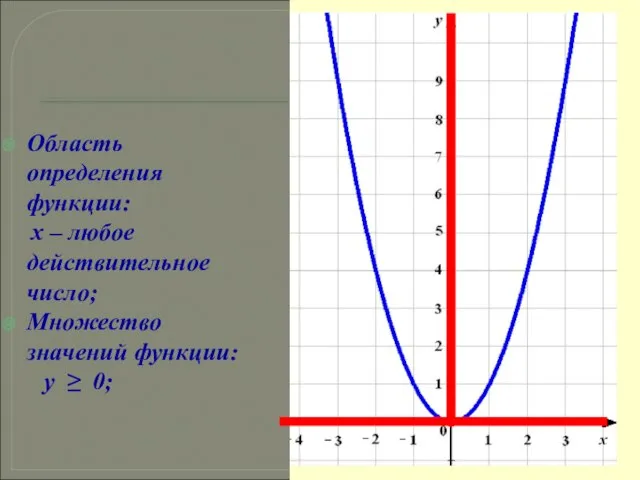
Область определения функции:
х – любое действительное число;
Множество значений функции:
у ≥ 0;

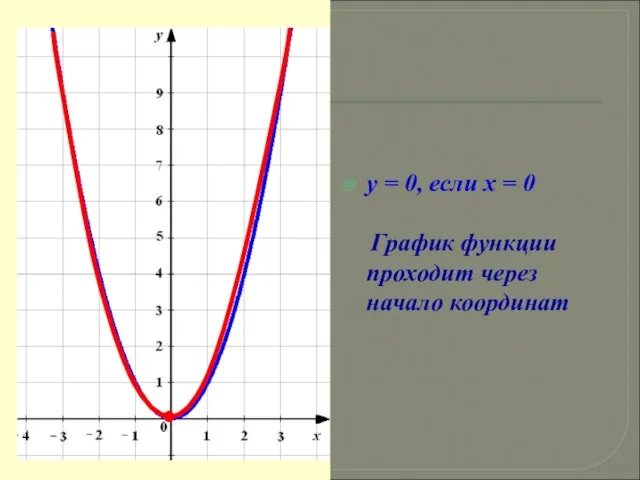
y = 0, если x = 0
График функции проходит через начало координат

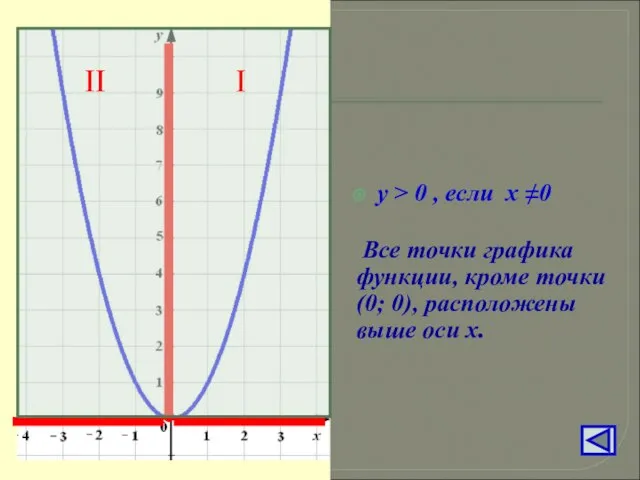
у > 0 , если х ≠0
Все точки графика
функции, кроме точки
(0; 0), расположены
выше оси х.
I
II

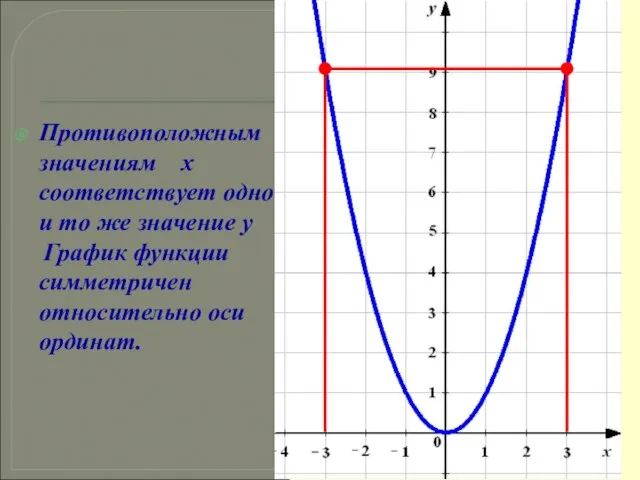
Противоположным значениям х соответствует одно и то же значение у
График функции симметричен относительно оси ординат.

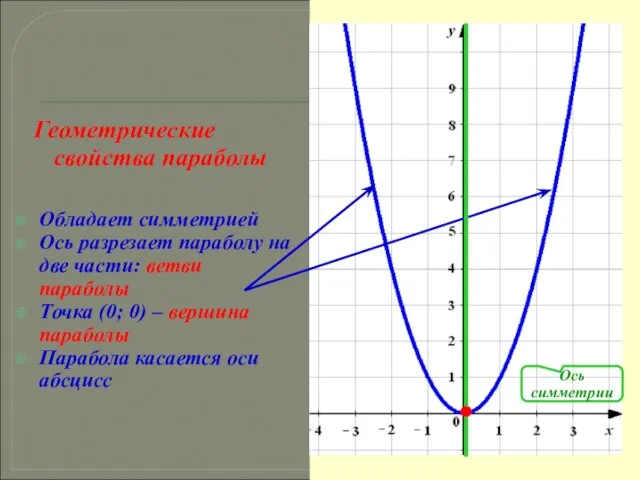
Геометрические свойства параболы
Обладает симметрией
Ось разрезает параболу на две части: ветви параболы
Точка (0; 0) – вершина параболы
Парабола касается оси абсцисс
Ось симметрии

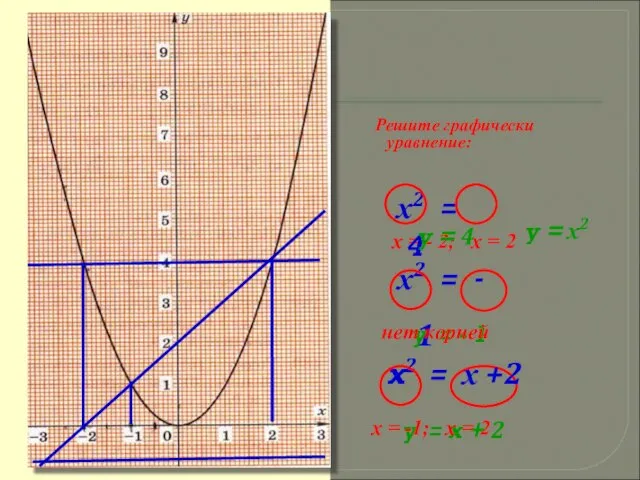
х = - 2; х = 2
Решите графически уравнение:
х2 = 4
х2 = - 1
x2 = х +2
y = - 1
y = x + 2
y = х2
y = 4
х = -1; х = 2
нет корней

У меня всё получилось!!!
Надо решить ещё пару примеров.
Ну кто придумал эту математику !