Содержание
- 2. Цель проекта: доказать, что теорему Пифагора можно изучать в 5 классе.
- 3. Задачи учебно-исследовательской работы: 1.изучить научную литературу; 2.познакомиться с геометрическими способами доказательствами теоремы; 3.составить презентацию для показа
- 4. А МОЖНО ЛИ ТЕОРЕМУ ПИФОГОРА ИЗУЧАТЬ В 5 КЛАССЕ ?
- 5. ДОКАЖЕМ, ЧТО ИЗ ДВУХ КВАДРАТОВ ОПРЕДЕЛЁННОЙ ПЛОЩАДИ МОЖНО СОСТАВИТЬ ТРЕТИЙ КВАДРАТ, ОПРЕДЕЛЕННОЙ ПЛОЩАДИ. Рассмотрим сначала более
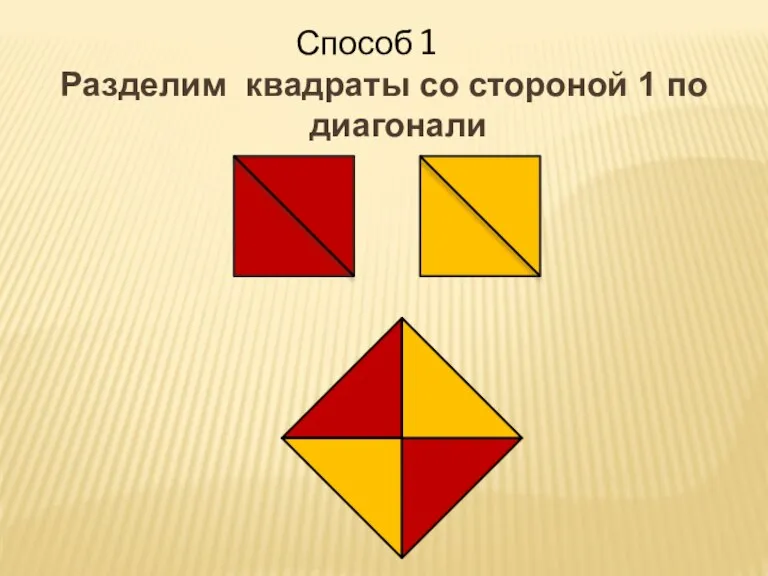
- 6. Разделим квадраты со стороной 1 по диагонали Способ 1
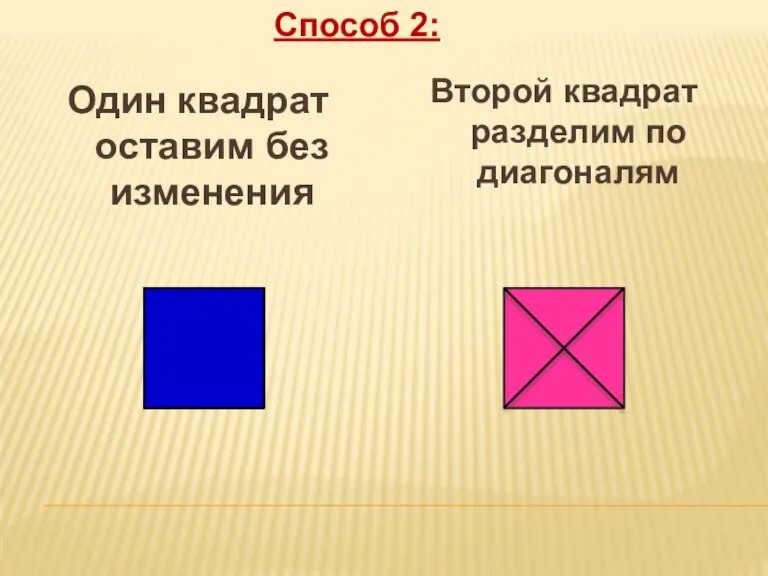
- 7. Второй квадрат разделим по диагоналям Способ 2: Один квадрат оставим без изменения
- 8. к первому квадрату приставим треугольники, получившиеся в результате деления второго квадрата
- 9. Составить из двух квадратов со стороной 1 и 2 третий квадрат.
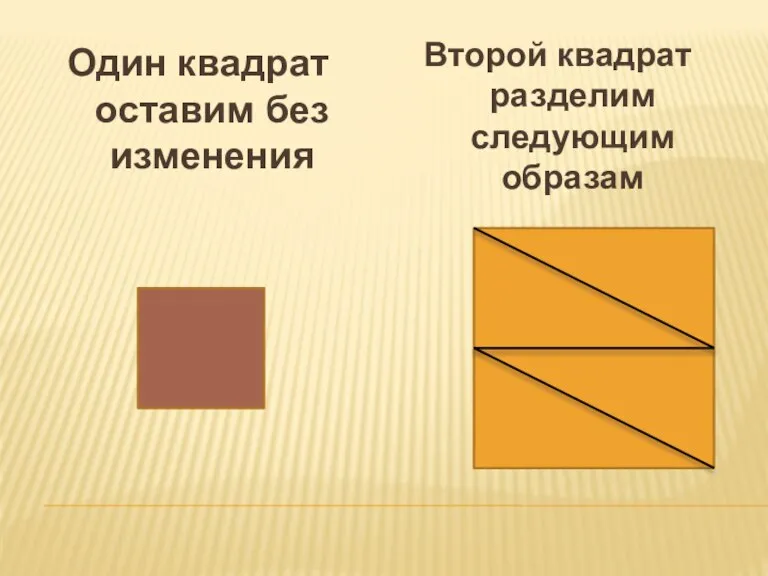
- 10. Второй квадрат разделим следующим образам Один квадрат оставим без изменения
- 11. к первому квадрату приставим треугольники, получившиеся в результате деления второго квадрата
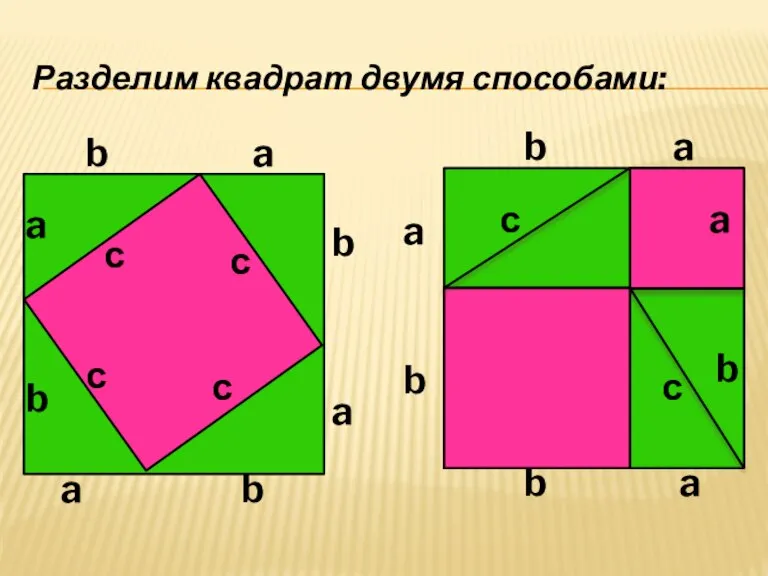
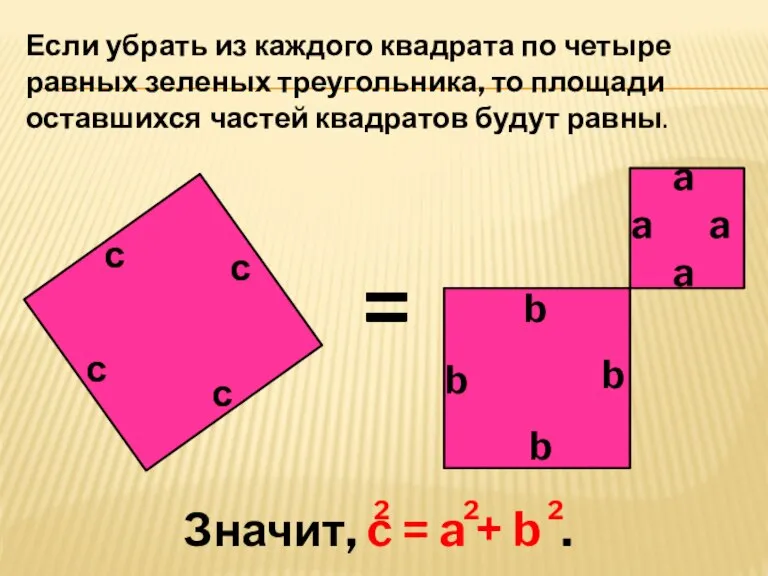
- 12. Разделим квадрат двумя способами: a a a a a a a a b b b b
- 13. Если убрать из каждого квадрата по четыре равных зеленых треугольника, то площади оставшихся частей квадратов будут
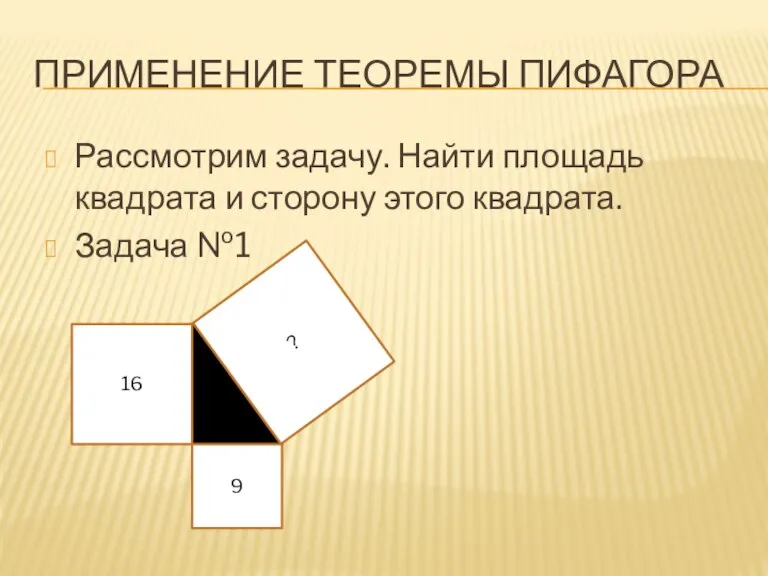
- 14. ПРИМЕНЕНИЕ ТЕОРЕМЫ ПИФАГОРА Рассмотрим задачу. Найти площадь квадрата и сторону этого квадрата. Задача №1 16 9
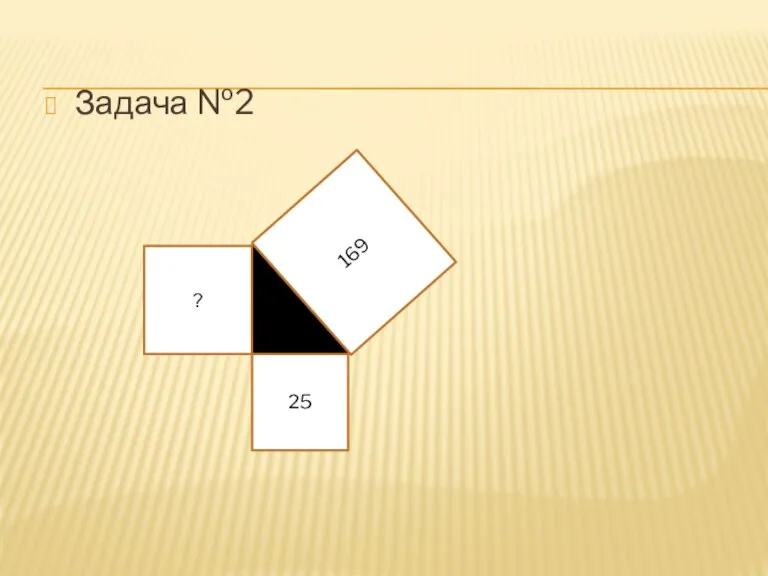
- 15. Задача №2 ? 25 169
- 16. ПИФАГОРОВЫ ТРОЙКИ ЧИСЕЛ 32 +42 =52 62 +82 =102 52 +122 =132 92 +122 =152 82
- 17. ПИФАГОР, ДОКАЗЫВАЯ СВОЮ ЗНАМЕНИТУЮ ТЕОРЕМУ, ПОСТРОИЛ ФИГУРУ, ГДЕ НА СТОРОНАХ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА РАСПОЛОЖЕНЫ КВАДРАТЫ. В НАШ
- 19. Скачать презентацию









 Движение и виды движения
Движение и виды движения 5_vektory
5_vektory Степень с целым показателем. Блиц-опрос
Степень с целым показателем. Блиц-опрос Классические алгоритмы на графах
Классические алгоритмы на графах Несложная тригонометрия
Несложная тригонометрия Презентация на тему Расположение точек относительно осей координат
Презентация на тему Расположение точек относительно осей координат  Логарифмические уравнения и методы их решения
Логарифмические уравнения и методы их решения Решение задач. Повторение пройденного
Решение задач. Повторение пройденного Золотое сечение
Золотое сечение Системы с цилиндрическим фазовым пространством
Системы с цилиндрическим фазовым пространством Таблица сложения
Таблица сложения Сумма углов в треугольнике
Сумма углов в треугольнике Метрология: применение математической статистики при измерениях и испытаниях
Метрология: применение математической статистики при измерениях и испытаниях Сечение тетраэдра
Сечение тетраэдра Математика. Занятие Число 7
Математика. Занятие Число 7 Решение задачи дуффинга регуляризованными методами неполного прогноза
Решение задачи дуффинга регуляризованными методами неполного прогноза Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений
Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений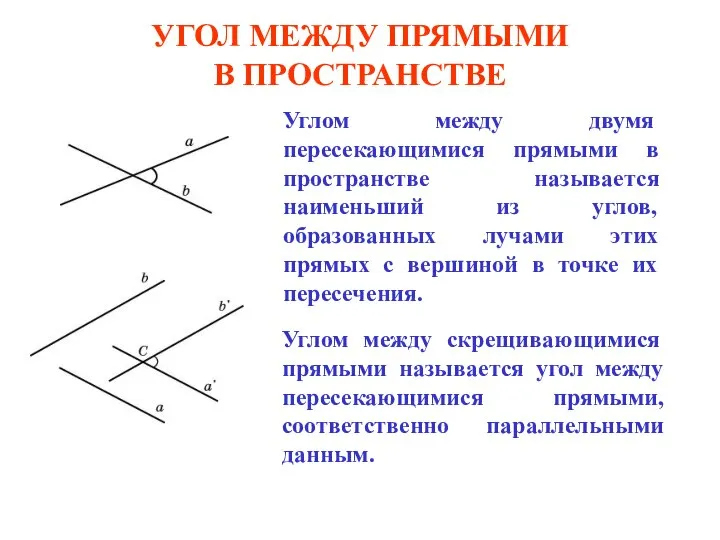 Угол между двумя прямыми в пространстве Вариант 2.ppt
Угол между двумя прямыми в пространстве Вариант 2.ppt Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Арифметический корень степени n
Арифметический корень степени n Обыкновенные дроби
Обыкновенные дроби Производная сложной функции
Производная сложной функции Симплекс метод. Лекция 5
Симплекс метод. Лекция 5 Свойства равнобедренных треугольников
Свойства равнобедренных треугольников Прикладной количественный анализ заголовков
Прикладной количественный анализ заголовков Сложение и вычитание чисел с разными знаками
Сложение и вычитание чисел с разными знаками Математическая викторина. 1 тур. Занимательные задачи
Математическая викторина. 1 тур. Занимательные задачи Решение системы уравнений первой степени с двумя неизвестными
Решение системы уравнений первой степени с двумя неизвестными