Содержание
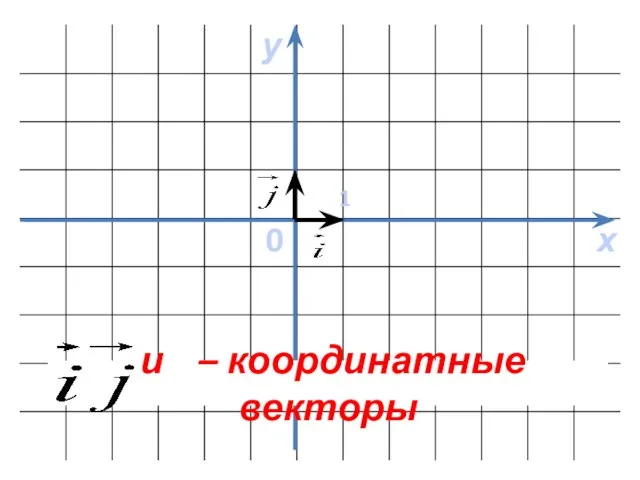
- 2. х у 0 1
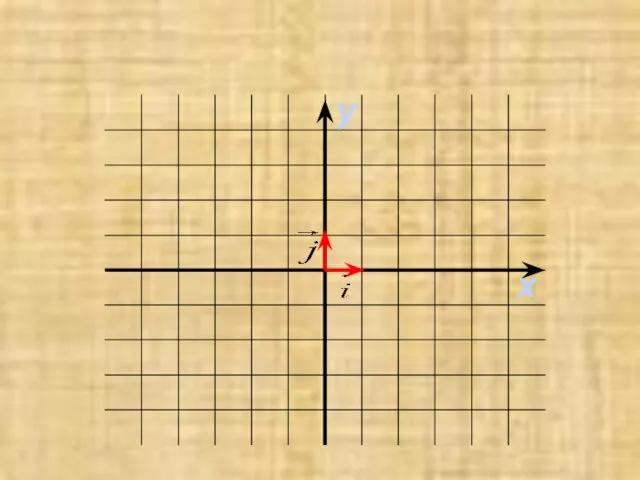
- 3. Любой вектор можно разложить по координатным векторам, при этом коэффициенты x и у в разложении являются
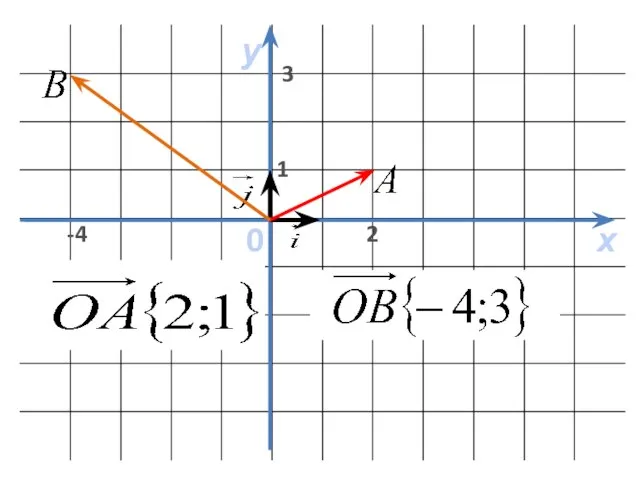
- 5. Вектор, начало которого совпадает с началом координат, называется радиус-вектором точки. Его координаты совпадают с координатами точки,
- 6. х у 0 1 -4 3 2
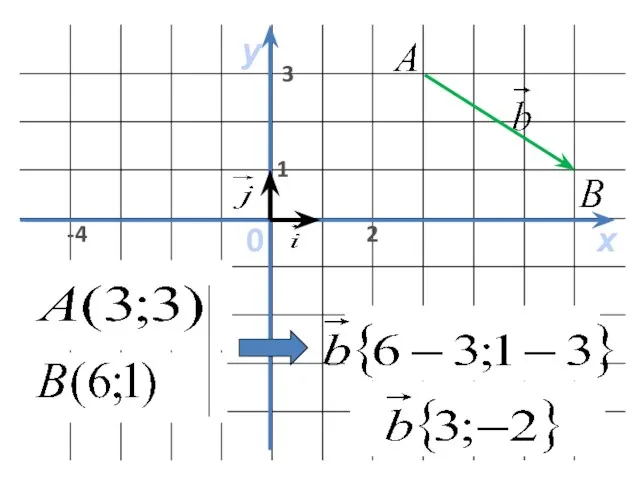
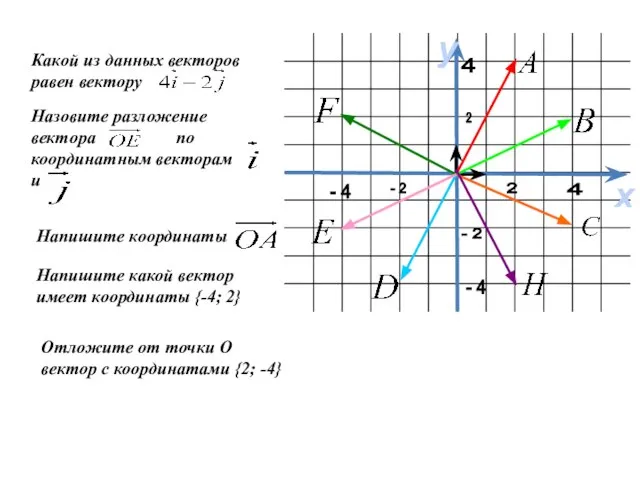
- 7. Чтобы найти координаты вектора, надо из соответствующей координаты конца вектора вычесть соответствующую координату начала. А(х1;у1) АВ{х2-х1;у2-у1}
- 8. х у 0 1 -4 3 2
- 10. Координаты равных векторов соответственно равны
- 11. 10. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
- 12. 20. Каждая координата разности двух или более векторов равна разности соответствующих координат этих векторов. 30. Каждая
- 13. Найдём координаты вектора
- 14. х у 4 - 2 - 2 2 2 - 4 - 4 4 Какой из
- 15. Даны векторы и Найти координаты векторов:
- 16. х у
- 19. Скачать презентацию

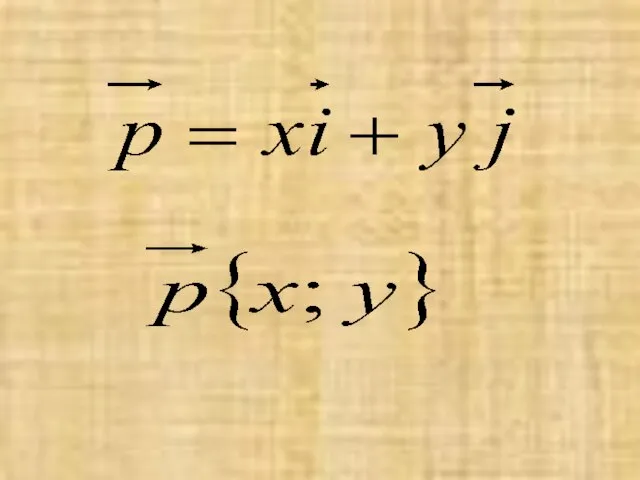









 Операции алгебры логики
Операции алгебры логики Измерительные приборы. Виды и предназначение
Измерительные приборы. Виды и предназначение user_file_5edd0051b6aa7
user_file_5edd0051b6aa7 Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости ЕГЭ Профиль. Решение задания №12
ЕГЭ Профиль. Решение задания №12 Расчет параметров слоев
Расчет параметров слоев Геометрические фигуры
Геометрические фигуры Презентация на тему Призма
Презентация на тему Призма  Квадратный корень
Квадратный корень Сравнение чисел
Сравнение чисел Устный счёт. Деление на двузначное число
Устный счёт. Деление на двузначное число Презентация на тему Начальные геометрические сведения
Презентация на тему Начальные геометрические сведения  04_8класс_Эталоны контроля качества продуктов труда. Измерительные приборы
04_8класс_Эталоны контроля качества продуктов труда. Измерительные приборы Элементы комбинаторики
Элементы комбинаторики Решение задач
Решение задач Рабочая программа внеурочной деятельности по математике для 5 класса Математическая мозаика
Рабочая программа внеурочной деятельности по математике для 5 класса Математическая мозаика Числа, кратные 2
Числа, кратные 2 Построение треугольника
Построение треугольника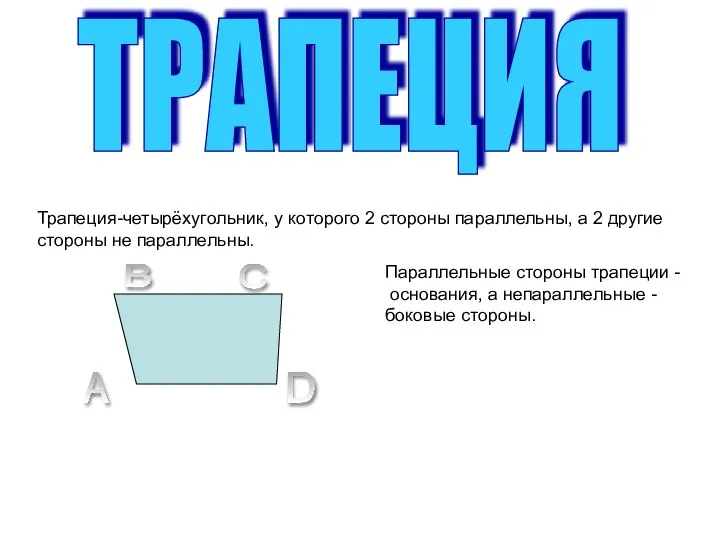 Трапеция
Трапеция Уходя, гасите свет. Математические расчеты
Уходя, гасите свет. Математические расчеты Дроби. Тест
Дроби. Тест Решение неравенств
Решение неравенств Деление суммы на число
Деление суммы на число Выполни задания в электронном дневнике
Выполни задания в электронном дневнике Угол между двумя плоскостями
Угол между двумя плоскостями Л11 Производная функции
Л11 Производная функции Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ В ПРОСТРАНСТВЕ
Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ В ПРОСТРАНСТВЕ  Целые уравнения
Целые уравнения