Решение задач

Оглавление
Задача № 1.21 .....………………………………………………………………………… 3
Задача № 1.22 …………………………………………………………………………….

Задача № 1.21
Чертеж:
Дано:
Окружность D=
△ ABC- правильный △
CD – высота
△CDE-правильный △
Окружность вписанная в △CDE
r-радиус
Найти: r
В окружность, диаметр которой равен √12, вписан правильный треугольник. На его высоте как на стороне построен другой правильный треугольник в который вписана новая окружность. Найдите радиус этой окружности.

Решение:
△ ABC :
AB=
Радиус r вписанной окружности :
r =
Ответ: 0,75

Задача № 1.22
В равносторонний треугольник вписана окружность. Этой окружности и сторон треугольника касаются три малые окружности . Найти сторону треугольника, если радиус малой окружности равен r.
Чертёж
Дано:
△ ABC-равносторонний △
Окружность R=OM вписана в △ABC
Окружности r=O1K
Найти: r-радиус

Решение:
1) a=AB сторона △ ABC
R=OM радиус вписанной окружности.
2) Проведём
R=OM в точке касания
r=ОК в точке касания
3) △ AOM ~△ AO1K
AO=

Ответ:

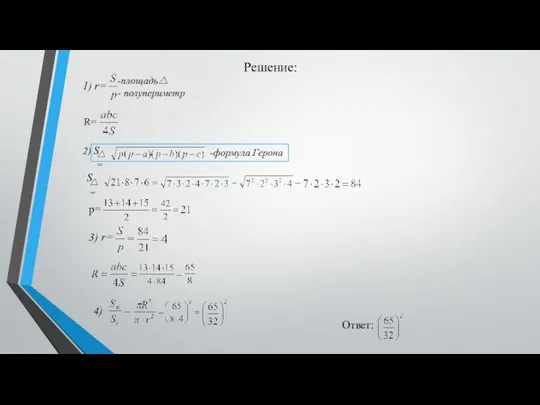
Задача №1.23
Стороны треугольника равны 13, 14 и 15 см. Найти отношение площадей описанного и вписанного в треугольник кругов.
Чертёж:
Дано:
△ ABC
a=AB=13 см
b=BC=14 см
c=AC=15 см
r- радиус вписанной окружности
R- радиус описанной окружности
Найти: Sокр. R
Sокр. r

Решение:
1) r=
-площадь
- полупериметр
△
R=
2) S
△=
-формула Герона
△=
S
p=
3) r=
4)
Ответ:

Задача № 1.52
Около круга радиуса 3 описан равнобедренный треугольник с острым углом 30° при основании. Определить стороны треугольника.
Дано:
△ ABC- равнобедренный
∠A= ∠C=30°
r =3 радиус вписанной окружности
Найти: стороны треугольника ABC
AB1,BC1,AC

Решение:
r = OE⊥ BC
∠ABC=180° - (30°+30°)= 120°
BD- высота, медиана, биссектриса.
△BOE : ∠OBE= 60°
∠OEB= 90°
∠BOE=30° ⇒ BE= (катет лежащий против ∠30°)
2) Из △BEO : BO²= OE²+BE²
BO²=