Угол между двумя плоскостями

Упражнение 1
Найдите угол φ между плоскостями, заданными уравнениями:
а) x = 0, y = 0;
б) x + y + z + 1 = 0, x + y – z – 1 = 0;
в) 2x + 3y + 6z – 5 = 0, 4x + 4y + 2z – 7 = 0.
Ответ: а) 90о;

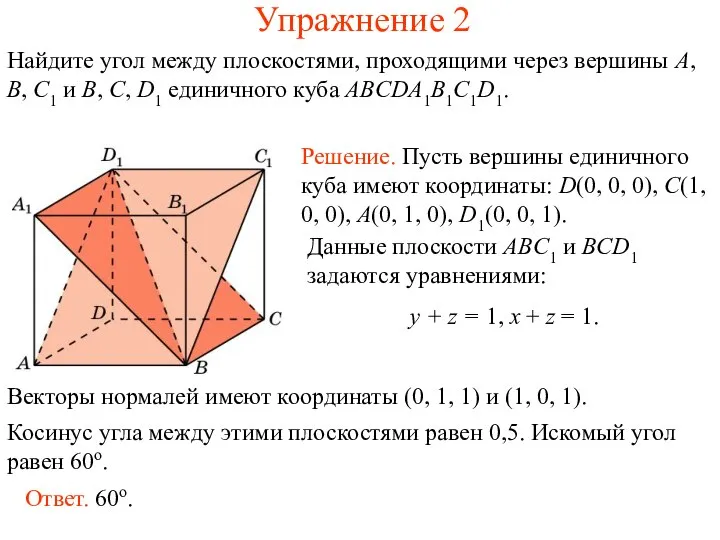
Упражнение 2
Найдите угол между плоскостями, проходящими через вершины A, B, C1 и B, C, D1 единичного куба ABCDA1B1C1D1.
Решение. Пусть вершины единичного куба имеют координаты: D(0, 0, 0), C(1, 0, 0), A(0, 1, 0), D1(0, 0, 1).
Векторы нормалей имеют координаты (0, 1, 1) и (1, 0, 1).
Данные плоскости ABC1 и BCD1 задаются уравнениями:
y + z = 1, x + z = 1.
Косинус угла между этими плоскостями равен 0,5. Искомый угол равен 60о.
Ответ. 60о.

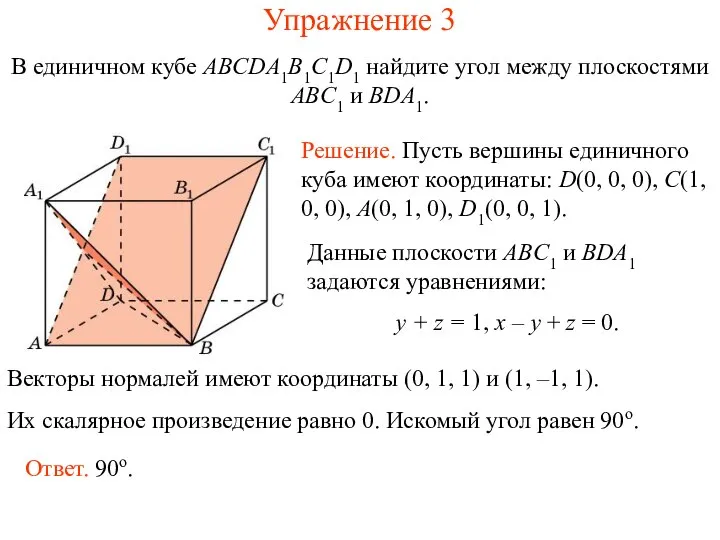
В единичном кубе ABCDA1B1C1D1 найдите угол между плоскостями ABC1 и BDA1.
Упражнение 3
Решение. Пусть вершины единичного куба имеют координаты: D(0, 0, 0), C(1, 0, 0), A(0, 1, 0), D1(0, 0, 1).
Векторы нормалей имеют координаты (0, 1, 1) и (1, –1, 1).
Данные плоскости ABC1 и BDA1 задаются уравнениями:
y + z = 1, x – y + z = 0.
Их скалярное произведение равно 0. Искомый угол равен 90о.
Ответ. 90о.

В единичном кубе ABCDA1B1C1D1 точка E – середина ребра AA1. Найдите угол φ между плоскостями ABC1 и B1D1E.
Упражнение 4
Решение. Пусть вершины единичного куба имеют координаты: D(0, 0, 0), C(1, 0, 0), A(0, 1, 0), D1(0, 0, 1).
Данные плоскости ABC1 и B1D1E задаются уравнениями:
y + z = 1, x – y – 2z + 2 = 0.
Ответ. 30о.

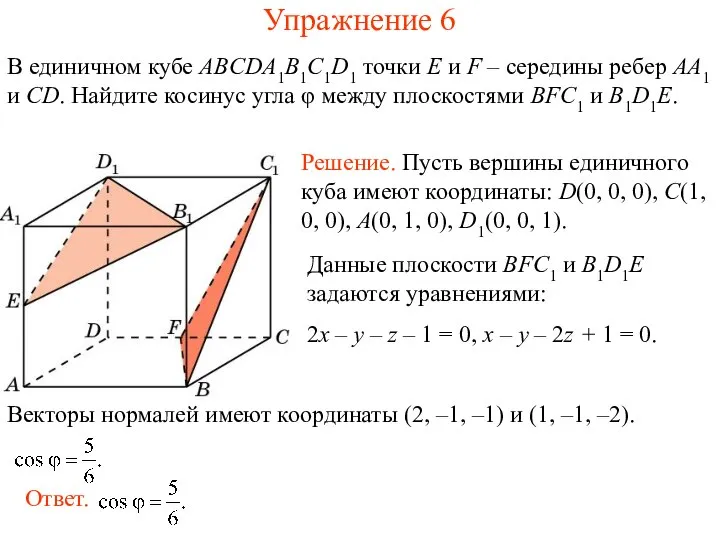
В единичном кубе ABCDA1B1C1D1 точки E и F – середины ребер AA1 и BB1. Найдите косинус угла φ между плоскостями ACF и B1D1E.
Упражнение 5
Решение. Пусть вершины единичного куба имеют координаты: D(0, 0, 0), C(1, 0, 0), A(0, 1, 0), D1(0, 0, 1).
Данные плоскости ACF и B1D1E задаются уравнениями:
x + y – 2z – 1= 0, x – y – 2z + 1 = 0.

В единичном кубе ABCDA1B1C1D1 точки E и F – середины ребер AA1 и CD. Найдите косинус угла φ между плоскостями BFC1 и B1D1E.
Упражнение 6
Решение. Пусть вершины единичного куба имеют координаты: D(0, 0, 0), C(1, 0, 0), A(0, 1, 0), D1(0, 0, 1).
Данные плоскости BFC1 и B1D1E задаются уравнениями:
2x – y – z – 1 = 0, x – y – 2z + 1 = 0.

В правильной 3-й призме ABCA1B1C1, ребра которой равны 1, найдите косинус угла между плоскостями ABC1 и AB1C1.
Упражнение 7

В правильной 3-й призме ABCA1B1C1, ребра которой равны 1, точки D и E – середины ребер AA1 и CC1. Найдите косинус угла между плоскостями ABE и DB1C1.
Упражнение 8

В правильной 4-й пирамиде SABCD, ребра которой равны 2, точки E, F и G – середины ребер AB, BC и SC. Найдите косинус угла между плоскостями SAD и EFG.
Упражнение 9

В правильной 4-й пирамиде SABCD, ребра которой равны 2, точки E, F – середины ребер SC, SD. Найдите косинус угла между плоскостями SAD и ABE.
Упражнение 10

В правильной 6-й призме A…F1, ребра которой равны 1, найдите косинус угла между плоскостями BDD1 и AFE1.
Упражнение 11

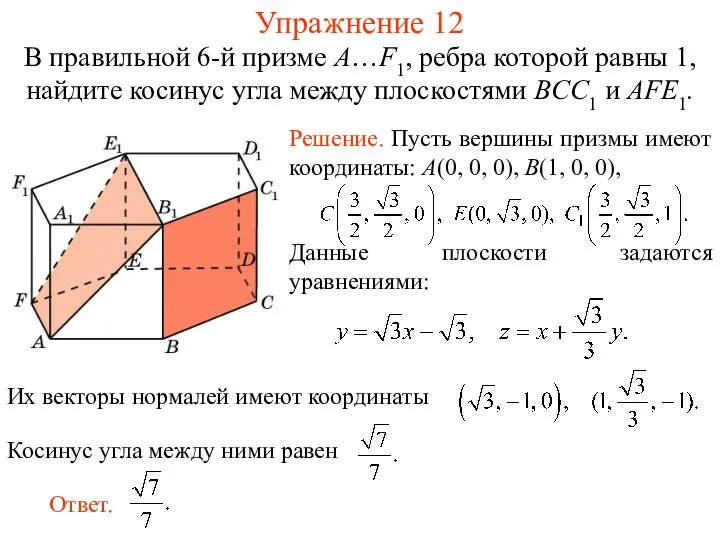
В правильной 6-й призме A…F1, ребра которой равны 1, найдите косинус угла между плоскостями BCC1 и AFE1.
Упражнение 12

В правильной 6-й пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между плоскостями SAF и SBD.
Упражнение 13