Содержание
- 2. 1. Производная функции одной переменной, геометрический и механический смысл. Механический смысл производной Пусть вдоль некоторой прямой
- 3. Поэтому под скоростью точки в момент времени t0 следует понимать предел средней скорости за промежуток времени
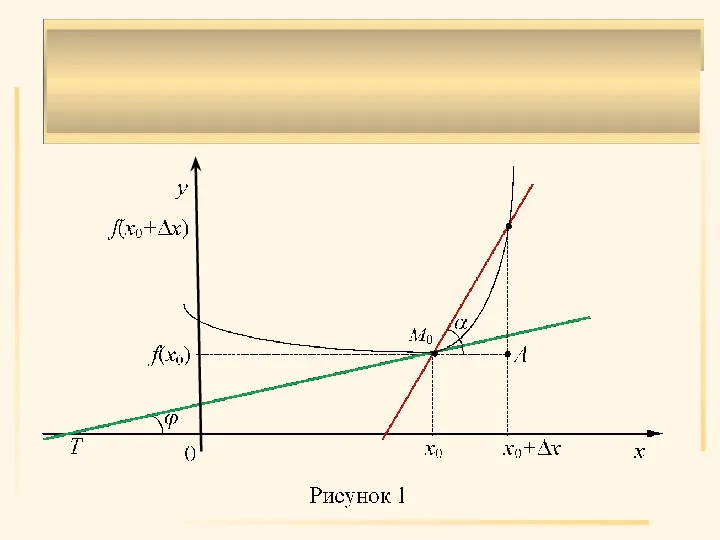
- 4. Геометрический смысл производной. Задача о касательной Найти уравнение касательной к кривой y=f(x) в точке M0(x0, f(x0)).
- 6. Определение 1. Предельное положение M0T секущей M0M при M→M0 (если оно существует) назовём касательной к кривой
- 7. Производная функции Определение 2. Производной функции f(x) в точке x0 называется предел отношения приращения функции к
- 8. 2. Дифференцируемость и непрерывность. Правила дифференцирования. Функция, имеющая производную (конечную) в каждой точке некоторого интервала, называется
- 9. Пример 1. Найти производные функций: y = C ; ; ; = С – С =
- 10. Теорема 1. Если функция f(x) имеет конечную производную в точке x0, то она непрерывна в этой
- 11. где α(Δx) – бесконечно малая величина при Отсюда: При и Следовательно, по определению непрерывности функции, функция
- 12. Обратная теорема, в общем случае, неверна. Например, функция непрерывна в точке x=0: Проверим, будет ли эта
- 13. Теорема 2. Если U(x) и V(x) имеют конечные производные в точке х0, то (V(x0)≠0) имеют конечные
- 14. Пример. Найти производную функции y = sin x. Докажем, что Доказательство: Так как , то (–∞;∞)=X.
- 15. 3. Производная сложной и обратной функций. Теорема 3. Если функция z=φ(x) имеет производную в точке x0,
- 16. Пример. Найти производную функции y = sin kx. Доказательство: По теореме о производной сложной функции имеем
- 17. Производная обратной функции Теорема 4. Если строго монотонная функция y=f(x) имеет для некоторого значения х∈(a;b) производную,
- 18. Таблица производных
- 19. Таблица производных
- 20. Таблица производных
- 21. Таблица производных
- 23. Скачать презентацию



















 Пропорции. Задачи
Пропорции. Задачи Презентация на тему Движение
Презентация на тему Движение  Сложение и вычитание числа 2
Сложение и вычитание числа 2 Математика
Математика Презентация на тему РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ
Презентация на тему РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ  Математика и спорт
Математика и спорт Разложение вектора по трём некомпланарным векторам
Разложение вектора по трём некомпланарным векторам Десятки, единицы, цифры
Десятки, единицы, цифры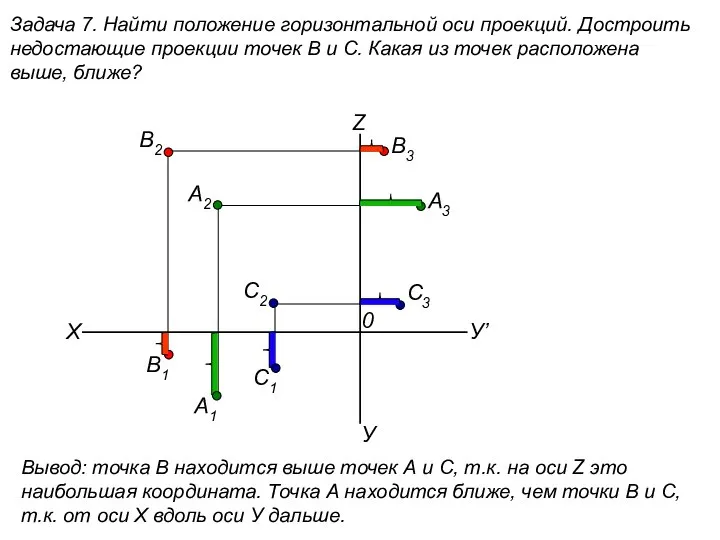 Найти положение горизонтальной оси проекций. Достроить недостающие проекции точек В и С. (задача 7)
Найти положение горизонтальной оси проекций. Достроить недостающие проекции точек В и С. (задача 7) Уравнение касательной к графику функции
Уравнение касательной к графику функции Решение уравнений. Первый и второй уровни
Решение уравнений. Первый и второй уровни Предельные величины, эластичности
Предельные величины, эластичности Математика – наука о наиболее общих и фундаментальных структурах реального мира
Математика – наука о наиболее общих и фундаментальных структурах реального мира Практическое применение треугольников в жизни
Практическое применение треугольников в жизни Освоение основных универсальных предметных знаний и умений в курсе технологии
Освоение основных универсальных предметных знаний и умений в курсе технологии Ряды динамики
Ряды динамики Презентация по математике "Знакомство с занимательной литературой по математике" -
Презентация по математике "Знакомство с занимательной литературой по математике" -  Простейшие функции и их графики
Простейшие функции и их графики Решение тригонометрических уравнений
Решение тригонометрических уравнений Логарифмические уравнения
Логарифмические уравнения Занимательные задачи
Занимательные задачи Комбинаторика
Комбинаторика Площадь параллелограмма. 8 класс
Площадь параллелограмма. 8 класс Соста числа 11
Соста числа 11 Обратные тригонометрические функции
Обратные тригонометрические функции Десятичный и натуральный логарифм
Десятичный и натуральный логарифм Параллельный перенос
Параллельный перенос Геймификация образовательного процесса на уроках математики с использованием двигательной активности
Геймификация образовательного процесса на уроках математики с использованием двигательной активности