Кривые второго порядка (1)

Окружность
Определение: Окружностью называется множество всех точек плоскости, равноудаленных от данной точки (центра окружности).
Если центр окружности совпадает с началом координат, то ее уравнение имеет вид:
(1)

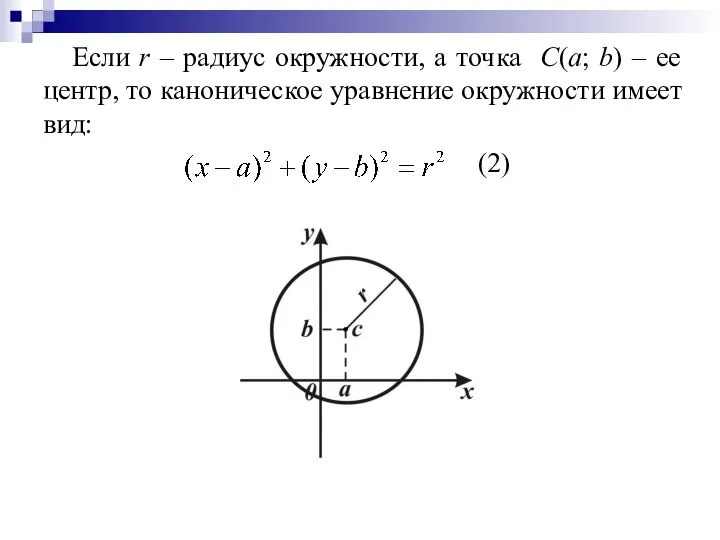
Если r – радиус окружности, а точка С(a; b) – ее центр, то каноническое уравнение окружности имеет вид:
(2)

Эллипс
Определение: Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между двумя фокусами.

По определению и, следовательно, или . Каноническое уравнение эллипса имеет вид:
(3)
где (4) , a – длина большой полуоси эллипса, b – длина малой полуоси эллипса ( ), с – половина расстояния между фокусами.
Оси координат являются осями симметрии эллипса.

– длина большой оси эллипса,
– длина малой оси эллипса,
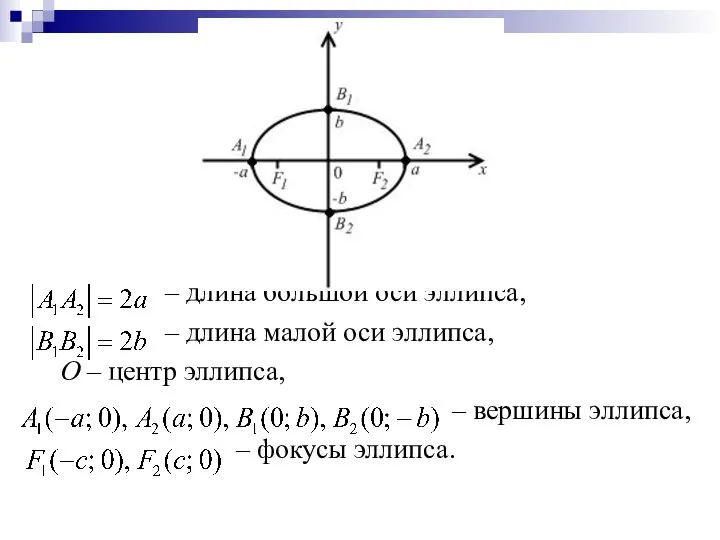
О – центр эллипса,
– вершины эллипса,
– фокусы эллипса.

Определение: Эксцентриситетом эллипса называется отношение половины расстояния между фокусами к длине большой полуоси эллипса: (5).
Так как , то .
Чем больше эксцентриситет, тем больше расстояние от центра эллипса до его фокусов и тем более «сплющен» эллипс; чем ближе эксцентриситет к 0, тем больше форма эллипса приближается к окружности.
При эллипс преобразуется в окружность, тогда и, следовательно, . Если , эллипс преобразуется в свою сдвоенную большую ось.

При эллипс расположен вдоль оси Оу. В этом случае оси Ох и Оу поменялись местами: большая ось и фокусы такого эллипса лежат на оси Оу, а малая ось на оси Ох.
Для такого эллипса:
– координаты фокусов;

Гипербола
Определение: Гиперболой называется множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между двумя фокусами.

По определению и, следовательно, или . Каноническое уравнение гиперболы имеет вид:
(6)
где (7) , a – длина действительной полуоси гиперболы, b – длина мнимой полуоси гиперболы, с – половина расстояния между фокусами.

Для построения гиперболы необходимо сначала построить осевой прямоугольник, затем провести диагонали этого прямоугольника, которые являются асимптотами гиперболы.
В силу симметрии гиперболы, она имеет две асимптоты: . Наличие асимптот и симметрии позволяют построить всю гиперболу.
Кривая состоит из двух не смыкающихся ветвей, лежащих в углах между асимптотами (8), и неограниченно приближающихся к этим прямым.

– длина действительной оси гиперболы,
– длина мнимой оси гиперболы,
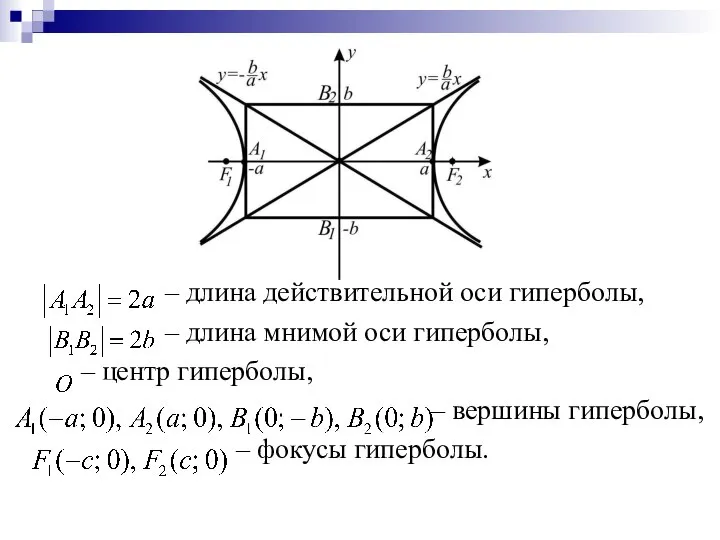
– центр гиперболы,
– вершины гиперболы,
– фокусы гиперболы.

Определение: Эксцентриситетом гиперболы называется отношение половины расстояния между фокусами к длине действительной полуоси гиперболы: (9).
Так как , то
Если , то гипербола называется равнобочной и ее асимптоты образуют прямой угол. Уравнение равнобочной гиперболы имеет вид:
(10)

Определение: Две гиперболы, у которых оси совпадают и равны, но действительная ось одной из них служит мнимой осью другой, и наоборот, называются сопряженными гиперболами.
Если уравнение одной из сопряженных гипербол
, то уравнение второй

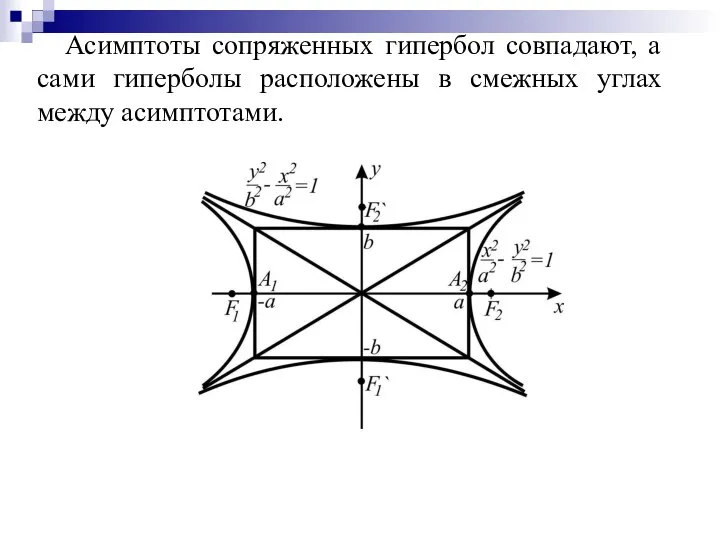
Асимптоты сопряженных гипербол совпадают, а сами гиперболы расположены в смежных углах между асимптотами.

Парабола
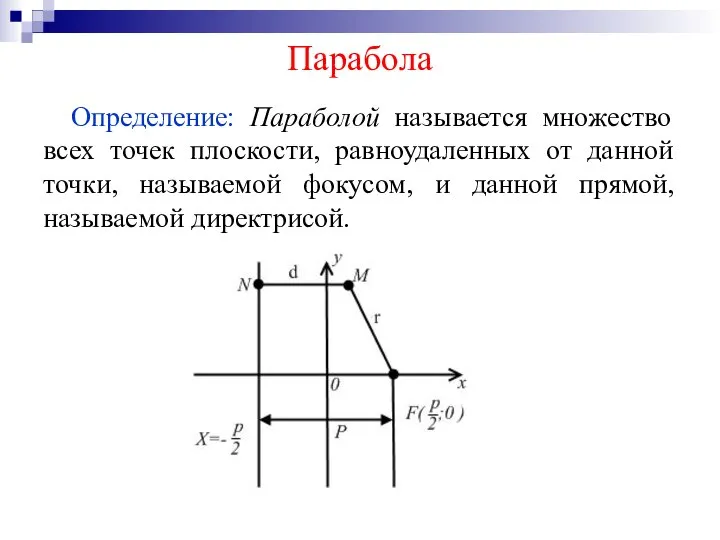
Определение: Параболой называется множество всех точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой.

Согласно определению точка М будет лежать на параболе, когда , где r – расстояние от точки до фокуса, d – расстояние от точки до директрисы.
Каноническое уравнение параболы имеет вид:
(11)
где р – параметр параболы (расстояние от фокуса до директрисы).
Параметр параболы характеризует ширину области ограниченной параболой. Чем больше р, тем шире распахнуты ветви параболы.

Парабола расположена симметрично относительно оси Ох , ветви направлены вправо.
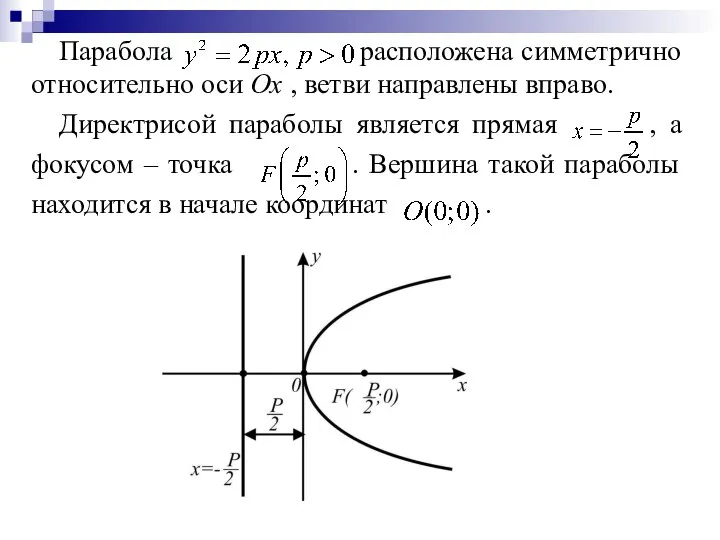
Директрисой параболы является прямая , а фокусом – точка . Вершина такой параболы находится в начале координат .

Парабола , расположена симметрично относительно оси Ох , ветви направлены влево.
Вершина параболы находится в точке . Директрисой параболы является прямая , а фокусом – точка .

Парабола , расположена симметрично относительно оси Оу , ветви направлены вверх.
Вершина параболы находится в точке . Директрисой параболы является прямая , а фокусом – точка .