Слайд 2Эллипсом называется геометрическое место точек, сумма расстояний от каждой из которых до

двух данных точек, называемых фокусами, есть величина постоянная (и большая, чем расстояние между фокусами).
Слайд 4Дано:
Эллипс
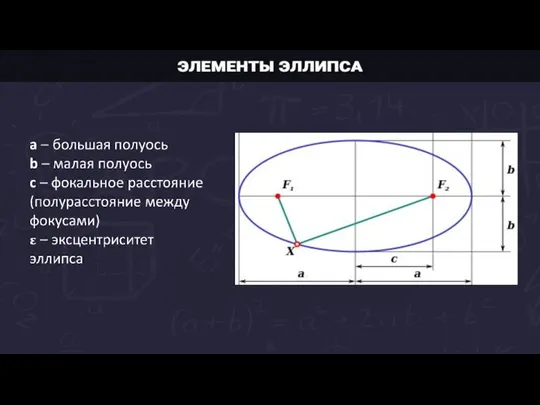
F1 и F2 – фокусы
a – большая полуось
c – половина расстояния между

Слайд 9Свойство 3: эллипс имеет две взаимно перпендикулярные оси симметрии.
Доказательство
В уравнение эллипса переменные

x и y входят только во второй степени, поэтому если точка M (x; y) принадлежит эллипсу, то точки M1 (x; -y) и M2 (-x; y) также принадлежат ему, т.к. их координаты удовлетворяют уравнению эллипса. Точка M1 симметрична M относительно оси Ох, а точка M2 – относительно Оy. Таким образом, эллипс имеет две оси симметрии, они взаимно перпендикулярны. Большая и малая полуоси эллипса лежат на его осях симметрии.
Слайд 10Свойство 4: эллипс имеет центр симметрии.
Доказательство
Если координаты точки M (x; y) удовлетворяют

уравнению эллипса, то этому же уравнению удовлетворяют и координаты точки N (-x; -y). Точка M симметричная точка N относительно начала координат. Таким образом, эллипс имеет центр симметрии.
Слайд 13Он получается в результате вращения эллипса вокруг одной из своих осей.
Величины a,
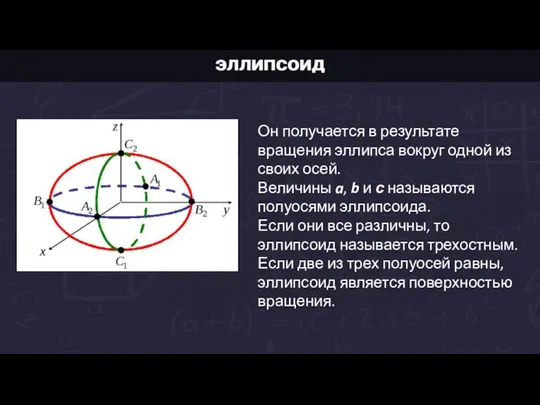
b и с называются полуосями эллипсоида.
Если они все различны, то эллипсоид называется трехостным.
Если две из трех полуосей равны, эллипсоид является поверхностью вращения.
Слайд 14Земля
Зеркало
Мяч для игры в американский футбол



















 Правильные многоугольники. Геометрия
Правильные многоугольники. Геометрия Центральная симметрия
Центральная симметрия Схема Горнера. Уильям Джордж Горнер
Схема Горнера. Уильям Джордж Горнер Признаки подобия треугольников
Признаки подобия треугольников Распределительное свойство умножения. Упрощение выражений
Распределительное свойство умножения. Упрощение выражений Длина окружности и площадь круга
Длина окружности и площадь круга Площади фигур
Площади фигур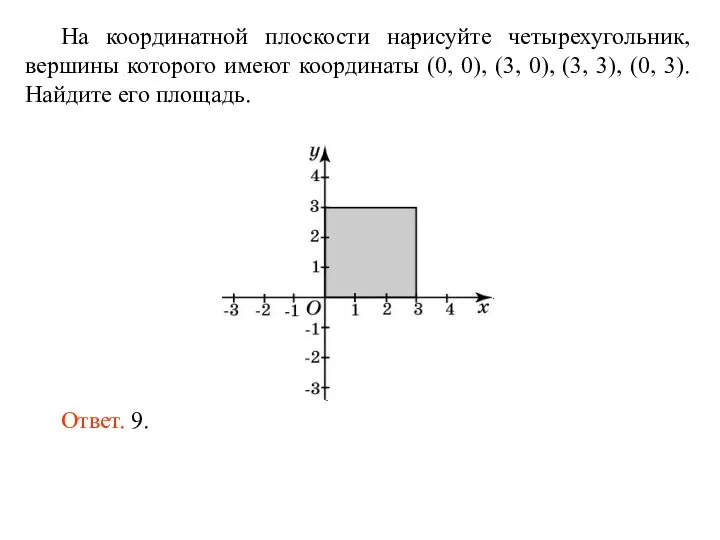 Площадь фигур на координатной плоскости
Площадь фигур на координатной плоскости Развитие интеллектуальных и творческих способностей одарённых учащихся в процессе преподавания математики
Развитие интеллектуальных и творческих способностей одарённых учащихся в процессе преподавания математики Составление и решение текстовых задач на увеличение и уменьшение числа на несколько единиц
Составление и решение текстовых задач на увеличение и уменьшение числа на несколько единиц Конусы в нашей жизни
Конусы в нашей жизни Вычитание вида 8 - ,9-
Вычитание вида 8 - ,9- Экстремумы (1)
Экстремумы (1) Онға дейінгі сандармен әрекеттер
Онға дейінгі сандармен әрекеттер Векторы в пространстве. Практическая работа
Векторы в пространстве. Практическая работа Степенная функция и её график
Степенная функция и её график Арифметическая прогрессия. ОБОБЩАЮЩИЙ УРОК
Арифметическая прогрессия. ОБОБЩАЮЩИЙ УРОК Четырехугольники: параллелограмм, трапеция, прямоугольник, ромб, квадрат
Четырехугольники: параллелограмм, трапеция, прямоугольник, ромб, квадрат Геометрия. Что значит это слово? часть 1
Геометрия. Что значит это слово? часть 1 Презентация на тему ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
Презентация на тему ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ  Арифметическая головоломка
Арифметическая головоломка Стереометрия. Аксиомы стереометрии. Часть 1
Стереометрия. Аксиомы стереометрии. Часть 1 Занимательная математика
Занимательная математика Вычисление вероятностей событий с использованием формулы полной вероятности и формулы Байеса
Вычисление вероятностей событий с использованием формулы полной вероятности и формулы Байеса Sam Signal Processing New2
Sam Signal Processing New2 Решение уравнения методом последовательных приближений
Решение уравнения методом последовательных приближений Свойства степени с натуральным показателем. 9 класс
Свойства степени с натуральным показателем. 9 класс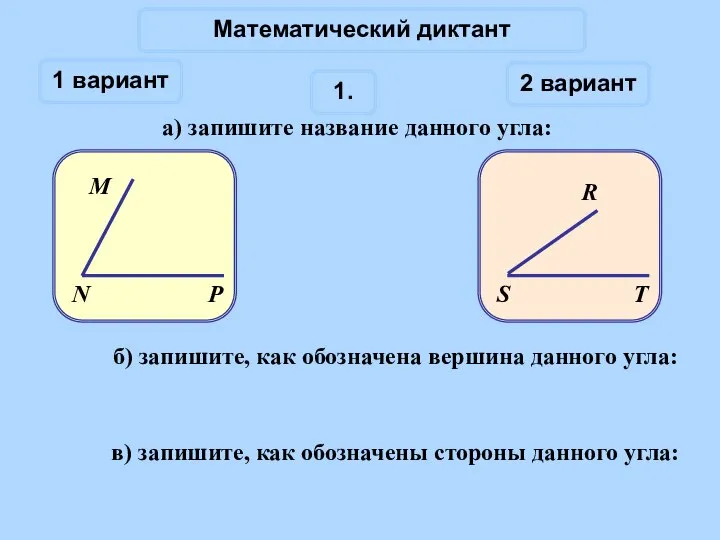 Углы. Математический диктант
Углы. Математический диктант