Содержание
- 2. Включить демонстрационный материал к задаче Выбрать задачу из общего списка (нажмите, чтобы перейти к ней) Задача
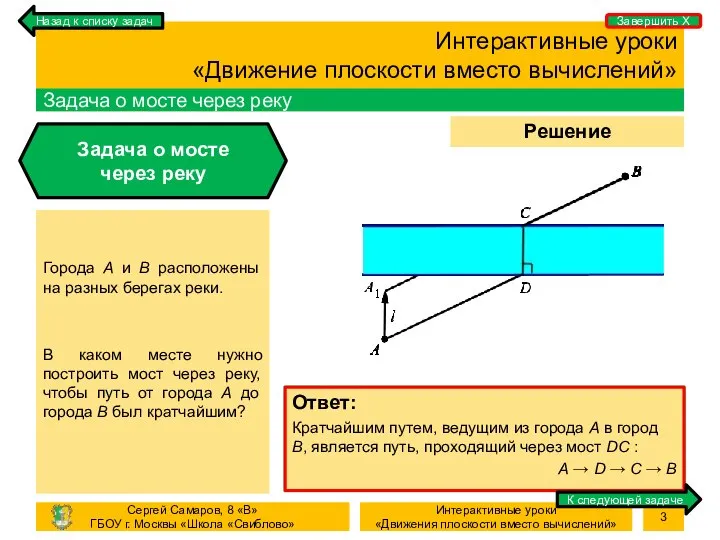
- 3. Процесс Решение задачи Интерактивные уроки «Движение плоскости вместо вычислений» Задача о мосте через реку Задача о
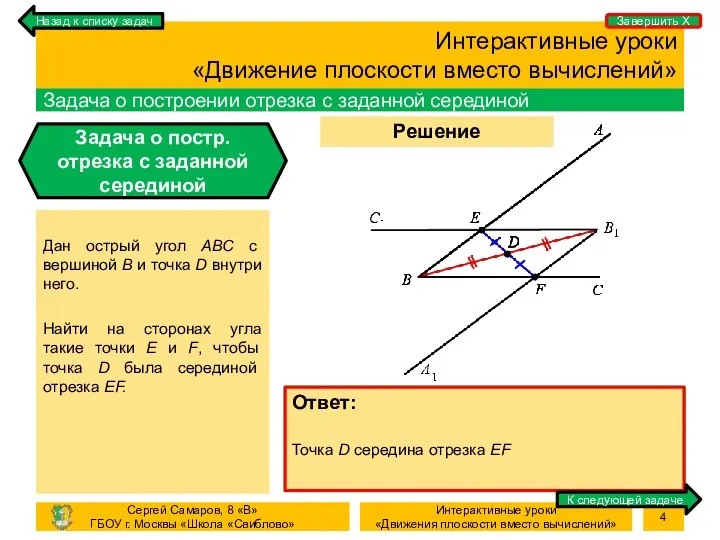
- 4. Процесс Решение задачи Интерактивные уроки «Движение плоскости вместо вычислений» Задача о построении отрезка с заданной серединой
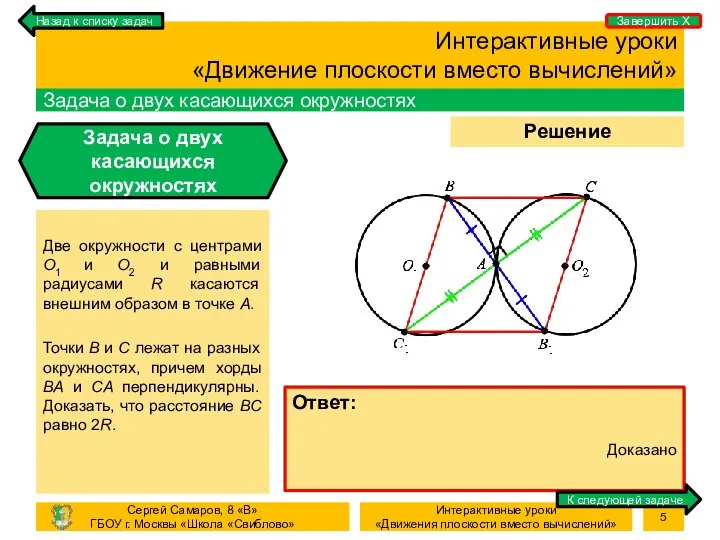
- 5. Процесс Решение задачи Интерактивные уроки «Движение плоскости вместо вычислений» Задача о двух касающихся окружностях Задача о
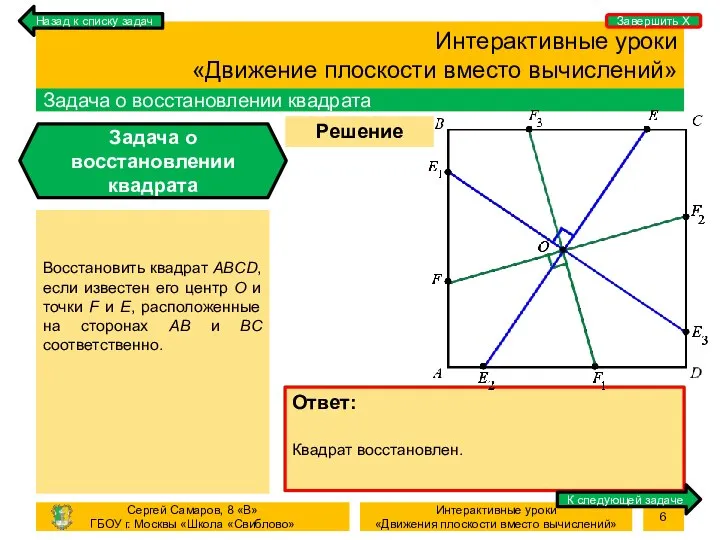
- 6. Процесс Решение задачи Интерактивные уроки «Движение плоскости вместо вычислений» Задача о восстановлении квадрата Задача о восстановлении
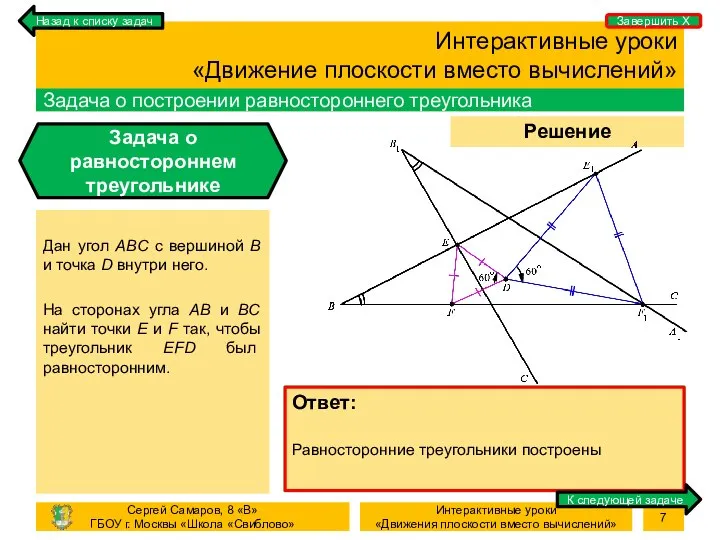
- 7. Процесс Решение задачи Интерактивные уроки «Движение плоскости вместо вычислений» Задача о построении равностороннего треугольника Задача о
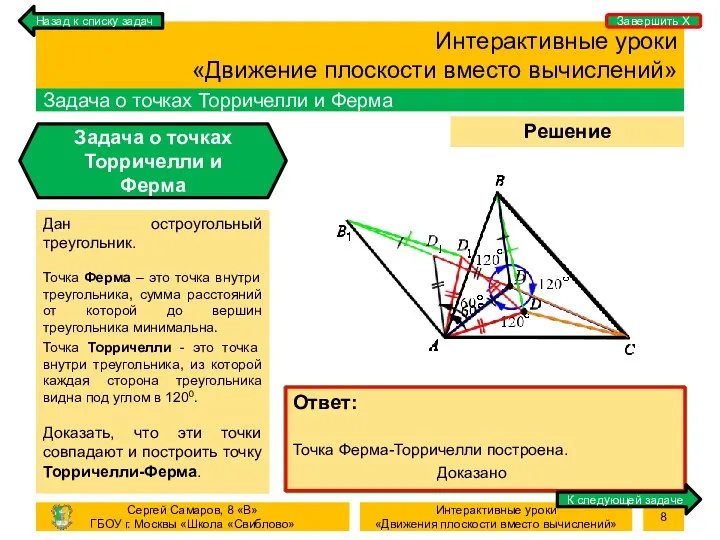
- 8. Процесс Определение точки Ферма (AD + BD + CD – мин.) Процесс Определение точки Торричелли Интерактивные
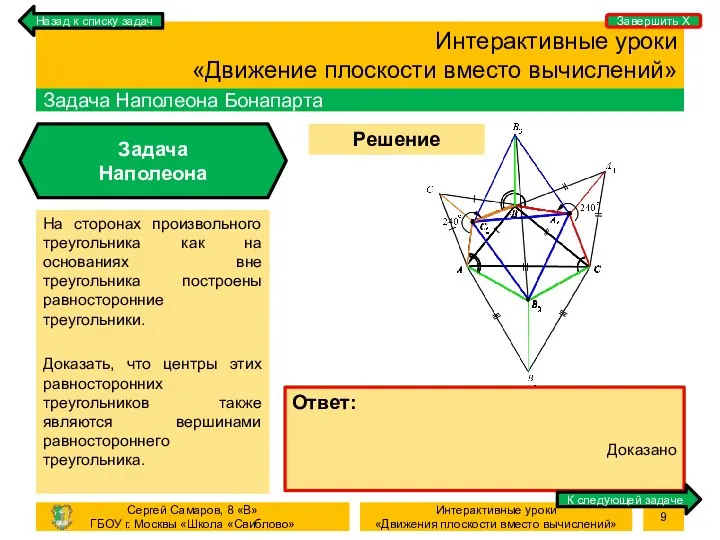
- 9. Процесс Решение задачи Интерактивные уроки «Движение плоскости вместо вычислений» Задача Наполеона Бонапарта Задача Наполеона На сторонах
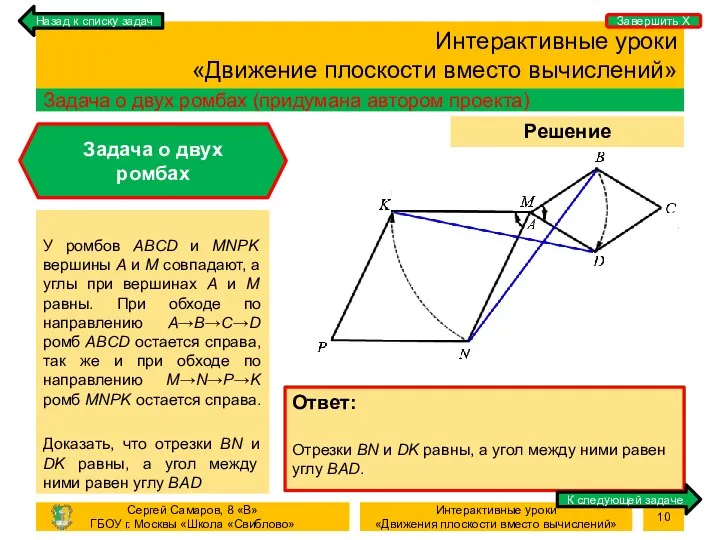
- 10. Процесс Решение задачи Интерактивные уроки «Движение плоскости вместо вычислений» Задача о двух ромбах (придумана автором проекта)
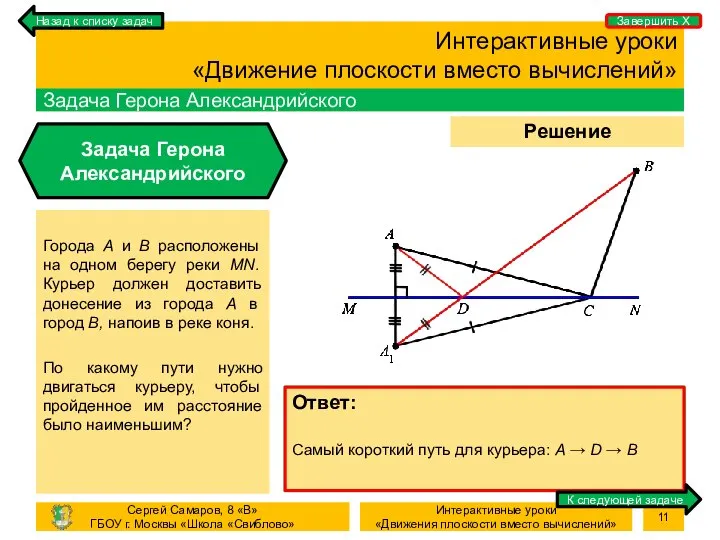
- 11. Процесс Решение задачи Интерактивные уроки «Движение плоскости вместо вычислений» Задача Герона Александрийского Задача Герона Александрийского Города
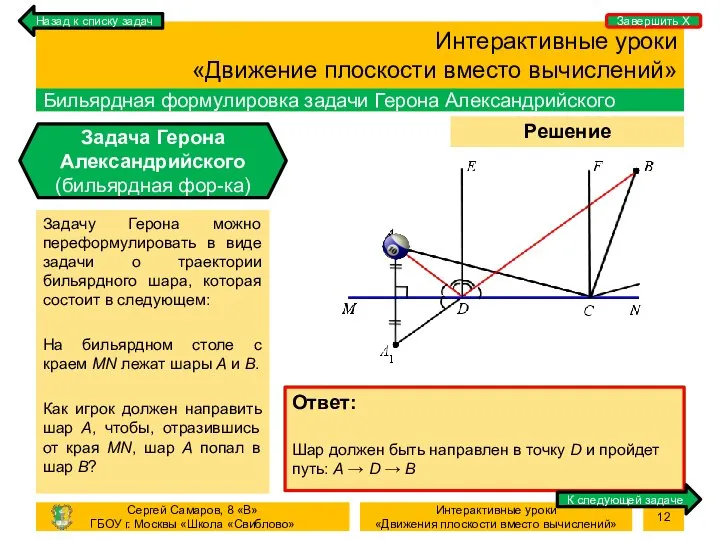
- 12. Процесс Решение задачи Интерактивные уроки «Движение плоскости вместо вычислений» Бильярдная формулировка задачи Герона Александрийского Задача Герона
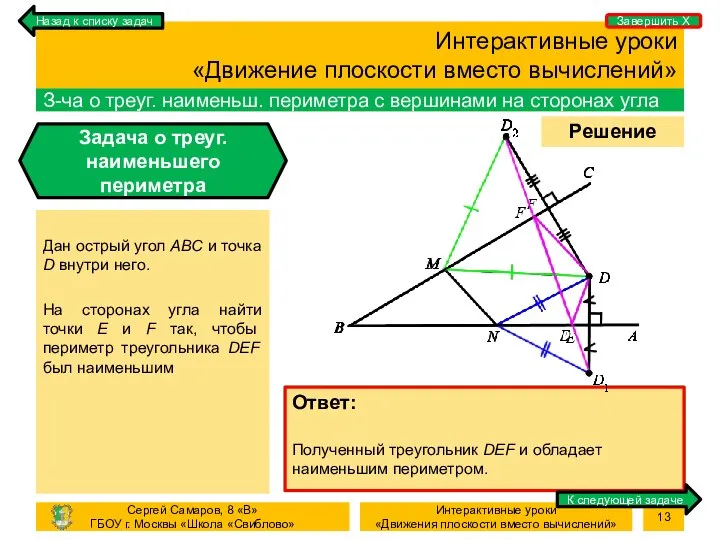
- 13. Процесс Решение задачи Интерактивные уроки «Движение плоскости вместо вычислений» З-ча о треуг. наименьш. периметра с вершинами
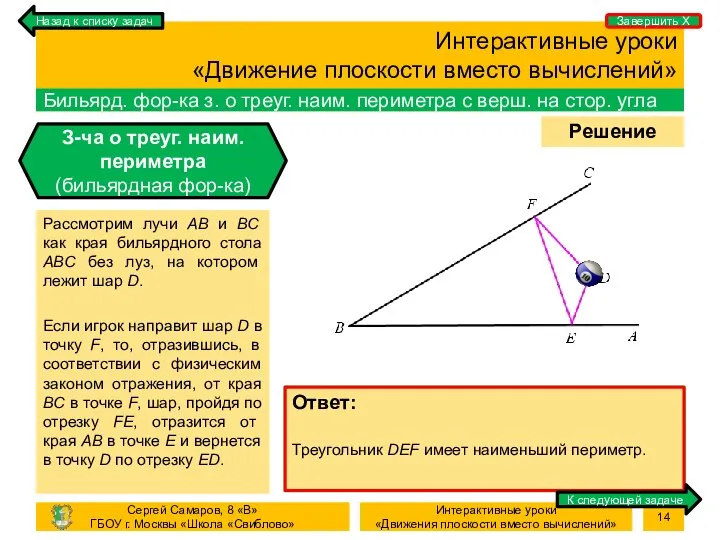
- 14. Процесс Решение задачи Интерактивные уроки «Движение плоскости вместо вычислений» Бильярд. фор-ка з. о треуг. наим. периметра
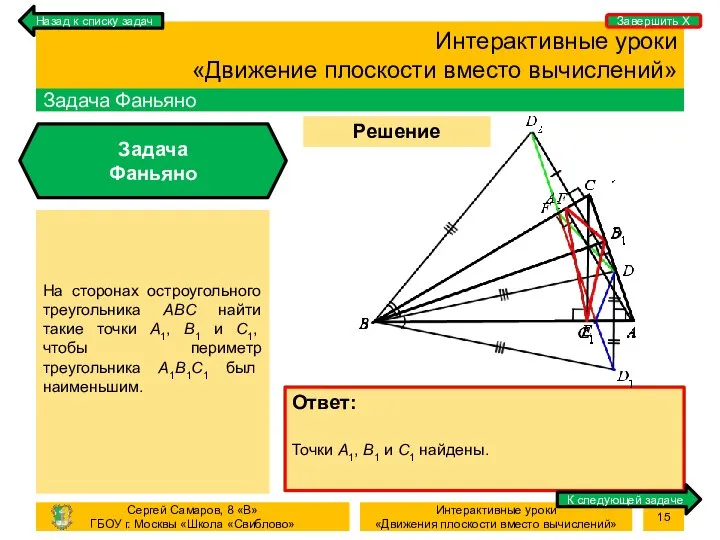
- 15. Процесс Решение задачи Интерактивные уроки «Движение плоскости вместо вычислений» Задача Фаньяно Задача Фаньяно На сторонах остроугольного
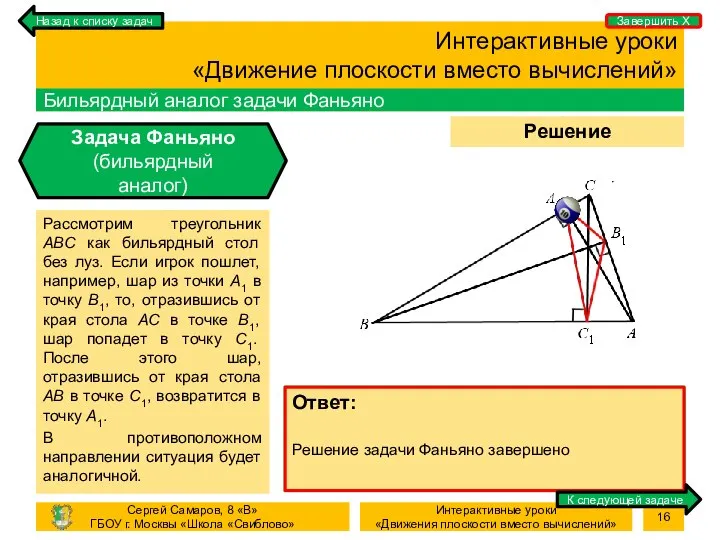
- 16. Процесс Решение задачи Интерактивные уроки «Движение плоскости вместо вычислений» Бильярдный аналог задачи Фаньяно Задача Фаньяно (бильярдный
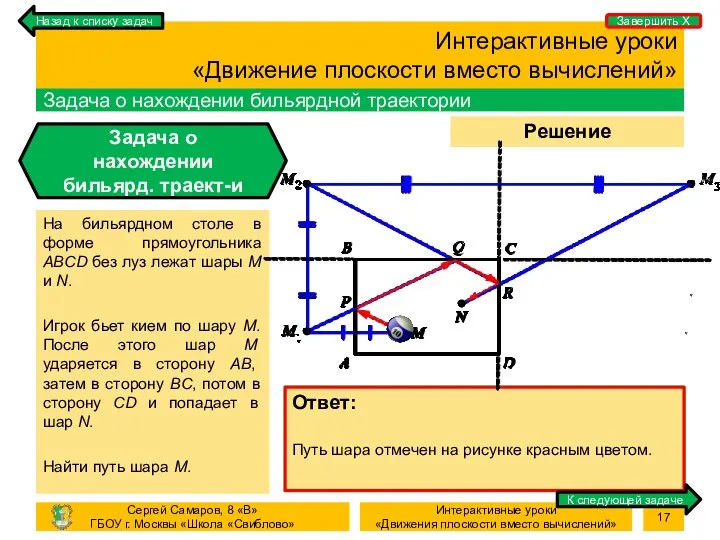
- 17. Процесс Решение задачи Интерактивные уроки «Движение плоскости вместо вычислений» Задача о нахождении бильярдной траектории Задача о
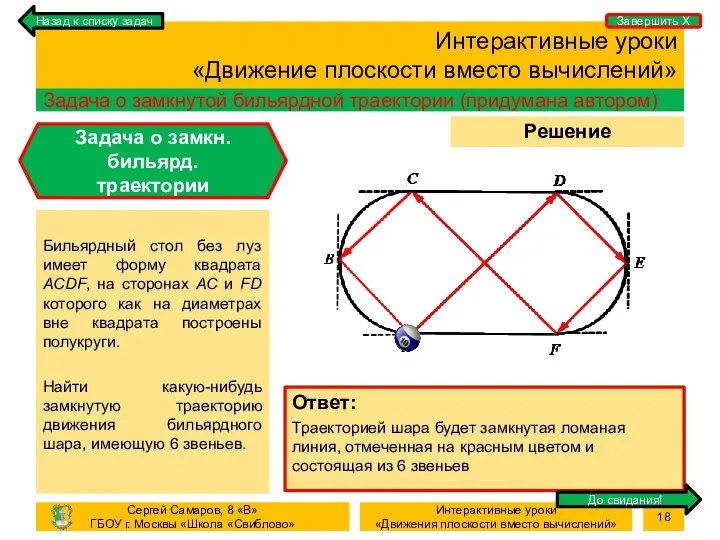
- 18. Процесс Решение задачи Интерактивные уроки «Движение плоскости вместо вычислений» Задача о замкнутой бильярдной траектории (придумана автором)
- 20. Скачать презентацию
 Математика. Составные высказывания
Математика. Составные высказывания Подготовка к ЕГЭ. Разбор типовых заданий В9 (производная,интеграл)
Подготовка к ЕГЭ. Разбор типовых заданий В9 (производная,интеграл) Ускоренное умножение
Ускоренное умножение Идеально сбалансированное дерево. Задание
Идеально сбалансированное дерево. Задание Дифференциальные уравнения. Лекция 3. Простейшие дифференциальные уравнения
Дифференциальные уравнения. Лекция 3. Простейшие дифференциальные уравнения Отрезок, луч, прямая. Графический диктант 1. 5 класс
Отрезок, луч, прямая. Графический диктант 1. 5 класс Примеры комбинаторных задач
Примеры комбинаторных задач Преобразование графиков функций. 8 класс
Преобразование графиков функций. 8 класс Золотое сечение
Золотое сечение Презентация на тему Медианы, биссектрисы и высоты треугольника (7 класс)
Презентация на тему Медианы, биссектрисы и высоты треугольника (7 класс)  Проверочная работа. 1 полугодие. 1 класс
Проверочная работа. 1 полугодие. 1 класс Базис векторного пространства
Базис векторного пространства Частное степеней
Частное степеней Презентация на тему Круговые диаграммы
Презентация на тему Круговые диаграммы  Усеченный цилиндр
Усеченный цилиндр Презентация на тему Логарифмы. Логарифмическая функция
Презентация на тему Логарифмы. Логарифмическая функция  Перспективная модель ЕГЭ по математике
Перспективная модель ЕГЭ по математике Поверхности второго порядка
Поверхности второго порядка Постановка задач исследования операций, основы математического программирования и методов оптимизации
Постановка задач исследования операций, основы математического программирования и методов оптимизации Математична статистика
Математична статистика Симметрия. 1 класс
Симметрия. 1 класс Чётные и нечётные функции
Чётные и нечётные функции Гистограммы. Представление статистических данных в графическом виде
Гистограммы. Представление статистических данных в графическом виде повторение 8 класса
повторение 8 класса Презентация на тему Функция в математике
Презентация на тему Функция в математике  Метрология: применение математической статистики при измерениях и испытаниях
Метрология: применение математической статистики при измерениях и испытаниях Векторы в пространстве
Векторы в пространстве Погрешности измерений
Погрешности измерений