Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля

Цель работы:
построение графиков графики функций, содержащие выражения под знаком модуля

Частный случай
(под знаком модуля одно выражение
и нет слагаемых без модуля)
1) построить график функции, опустив знак модуля
2) отобразить симметрично оси Ох часть графика, расположенного в области отрицательных значений у.

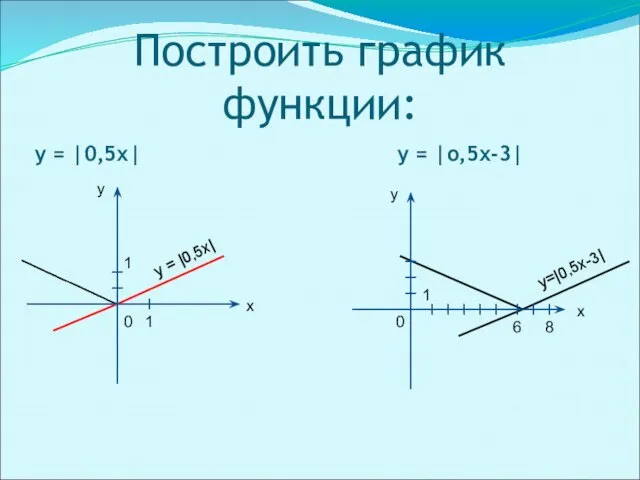
Построить график функции:
у = |0,5х|
у = |о,5х-3|
у = |0,5х|
у=|0,5х-3|

Построение графиков, содержащих выражения под знаком модуля
1) найти корни выражений, стоящих под знаком модуля;
2) на числовой прямой проставить эти корни;
3) в каждом промежутке определить вид функции;
4) построить график в каждом промежутке.

Построить график функции:
у =|3х+4|-2
Решение: 3х+4=0
х =
Координатная плоскость разбивается прямой х =
на две полуплоскости:
1) х<
у =-(3х+4)-2 х у
у =-3х-6 -2 0
-3 3
2) х≥
у=3х+4-2 х у
у=3х+2 -1 -1
0 2
у=|3х+4|-2

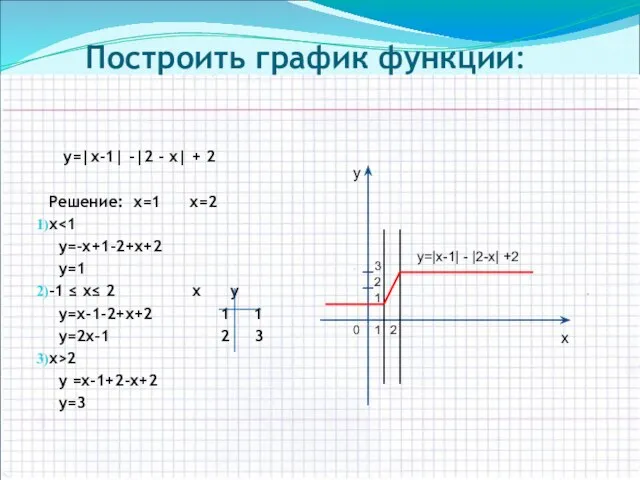
2
Построить график функции:
у=|х-1| -|2 - х| + 2
Решение: х=1 х=2
х<1
у=-х+1-2+х+2 у=1
-1 ≤ х≤ 2 х у
у=х-1-2+х+2 1 1
у=2х-1 2 3
х>2
у =х-1+2-х+2
у=3

a) y=|х-1|+|х-2|+х слайд №9
b) y=|3х|-3х слайд №10
c) y=|х-3|+|1-х|+4 слайд №10
d) y=|5-х|-|2-х|-3 слайд №11
e) y=7 -|х-1|+|х+5| слайд №11
f) y=|х-5|+|5-х| слайд №12f) y=|х-5|+|5-х| слайд №12 f) y=|х-5|+|5-х| слайд №12
k) y=-|3-х|+|2-х|-3 слайд №12k) y=-|3-х|+|2-х|-3 слайд №12
l) y=| х-2|+|3+ х|-3 слайд №13
Практические упражнения

a) у=|х - 1|+|2 - х| +2
Решение:
х=1; х=2
х< 1
у=-х+1-2+х+2
у=1
1≤х≤ 2 у=х-1-2+х+2
у=2х -1
х>2
у=х-1+2-х+2
у=3
у=|х-1|-|2-х|+2
х у
1
2 3

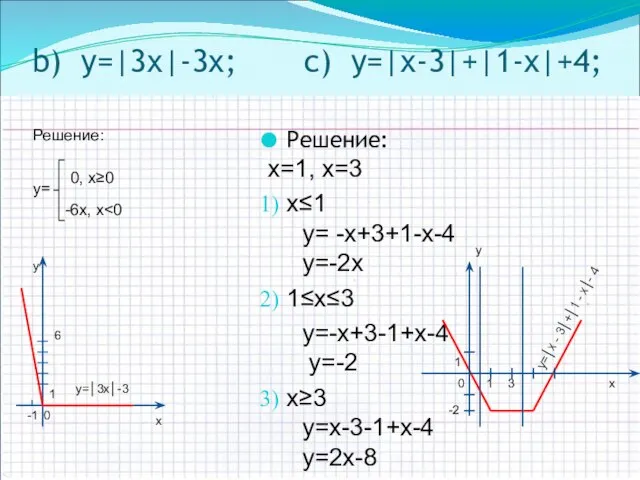
Решение:
х=1, х=3
x≤1
y= -x+3+1-x-4
y=-2x
1≤x≤3
y=-x+3-1+x-4
y=-2
x≥3
y=x-3-1+x-4
y=2x-8
b) y=|3х|-3х; c) y=|х-3|+|1-х|+4;
Решение:
0, х≥0
-6х, х<0
y=│3x│-3
y=│x - 3│+│1 - x│- 4

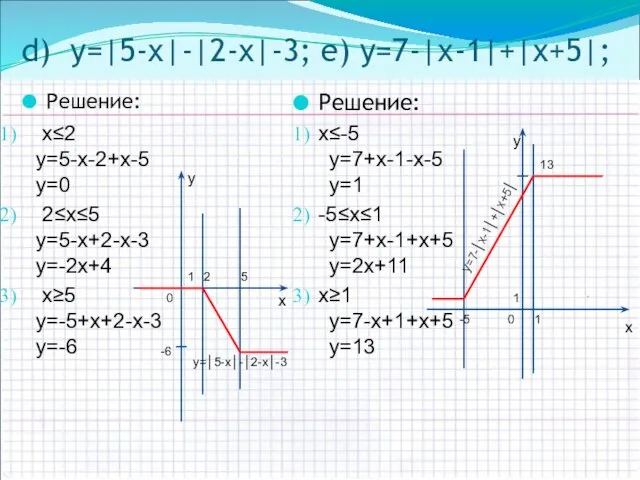
d) y=|5-х|-|2-х|-3; e) y=7-|х-1|+|х+5|;
Решение:
х≤-5
y=7+х-1-х-5
y=1
-5≤х≤1
y=7+х-1+х+5
y=2х+11
x≥1
y=7-х+1+х+5
y=13
Решение:
х≤2
y=5-х-2+х-5
y=0
2≤х≤5 y=5-х+2-х-3
y=-2х+4
x≥5
y=-5+х+2-х-3
y=-6
y=7-│x-1│+│x+5│
y=│5-x│-│2-x│-3

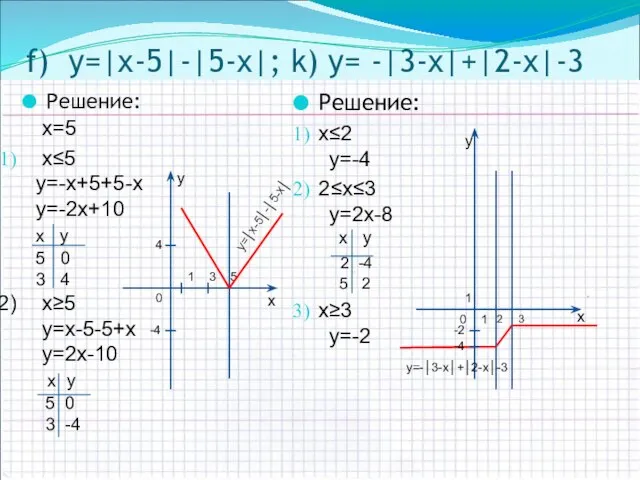
f) y=|х-5|-|5-х|; k) y= -|3-х|+|2-х|-3
Решение:
х≤2
y=-4
2≤х≤3
y=2х-8
x y
2 -4
5 2
x≥3
y=-2
Решение:
x=5
х≤5
y=-х+5+5-х
y=-2х+10
x y
5 0
3 4
x≥5
y=x-5-5+x
y=2x-10
x y
5 0
3 -4
y=-│3-x│+│2-x│-3
y=│x-5│-│5-x│

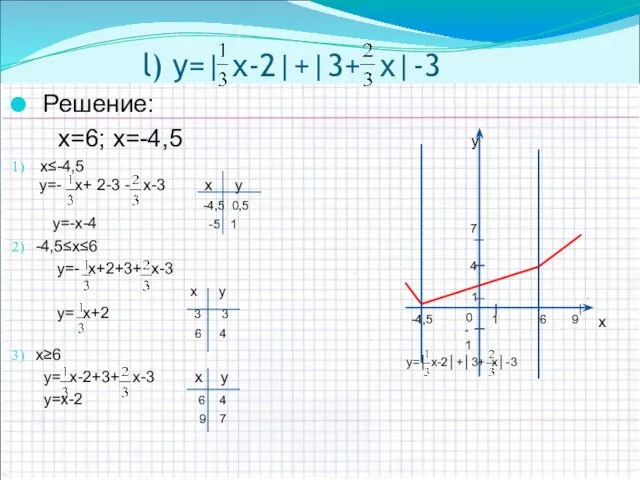
l) y=| х-2|+|3+ х|-3
Решение:
x=6; х=-4,5
х≤-4,5
y=- х+ 2-3 - х-3 х у
-4,5 0,5
y=-х-4 -5 1
-4,5≤х≤6
y=- x+2+3+ x-3
х у
y= x+2 3 3
6 4
x≥6
y= x-2+3+ x-3 х у
y=x-2 6 4
9 7
y=│ x-2│+│3+ x│-3

Вывод:
Решите уравнение: │х-3│+│1-х│=4 (х=3; х=1)
Постройте график функции: y= │х-3│+│1-х│- 4
Имея корни решенного уравнения и рассматривая график построенной функции, делаем вывод: корни данного уравнения – это координаты точки пересечения графика с осями координат.
Таким образом строим графики функций, содержащие выражения под знаком модуля опираясь на решение уравнения, содержащего выражения под знаком модуля.