Содержание
- 2. Квадрат - это четырехугольник, у которого все четыре стороны и углы одинаковы. Квадраты отличаются между собой
- 3. Основные свойства квадрата
- 4. 1. Все четыре стороны квадрата имеют одинаковую длину, то есть они равны: AB = BC =
- 5. 2. Противоположные стороны квадрата параллельны: AB||CD, BC||AD
- 6. 3. Все четыре угла квадрата прямые: ∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
- 7. 4. Сумма углов квадрата равна 360 градусов: ∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
- 8. 5. Диагонали квадрата имеют одинаковой длины: AC = BD
- 9. 6. Каждая диагональ квадрата делит квадрат на две одинаковые симметричные фигуры
- 10. 7. Диагонали квадрата пересекаются под прямым углом, и разделяют друг друга пополам: 7. Диагонали квадрата пересекаются
- 11. 8. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности
- 12. 9. Каждая диагональ делит угол квадрата пополам, то есть они являются биссектрисами углов квадрата: ΔABC =
- 13. 10. Обе диагонали разделяют квадрат на четыре равные треугольника, причем эти треугольники одновременно и равнобедренные и
- 14. Диагональ квадрата Диагональю квадрата называется любой отрезок, соединяющий две вершины противоположных углов квадрата. Диагональ любого квадрата
- 15. Формула диагонали квадрата через площадь квадрата: d = √2S Формула диагонали квадрата через периметр квадрата: Формула
- 16. Периметр квадрата Периметром квадрата называется сумма длин всех сторон квадрата.
- 17. Формула периметра квадрата через сторону квадрата P = 4a Формула периметра квадрата через площадь квадрата: P
- 18. Площадь квадрата Площадью квадрата называется пространство, ограниченное сторонами квадрата, то есть в пределах периметра квадрата. Площадь
- 19. Формула площади квадрата через сторону квадрата: S = a2 Формула площади квадрата через периметр квадрата: Формула
- 20. Окружность описанная вокруг квадрата Кругом описанным вокруг квадрата называется круг проходящий через четыре вершины квадрата и
- 22. Скачать презентацию

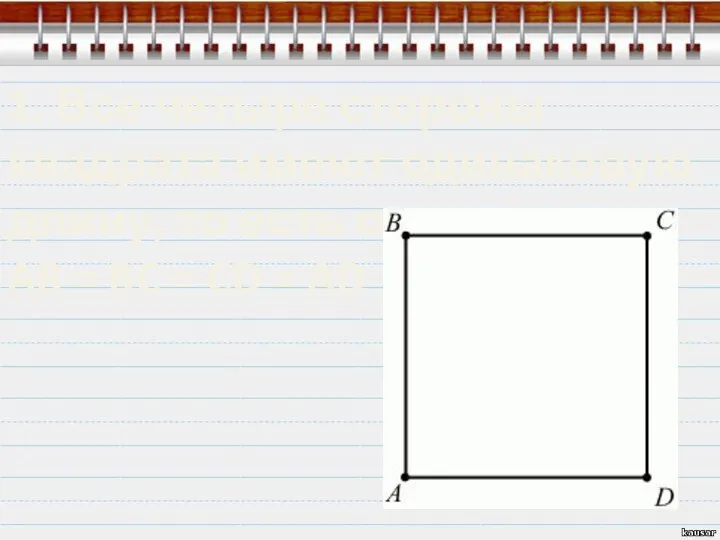
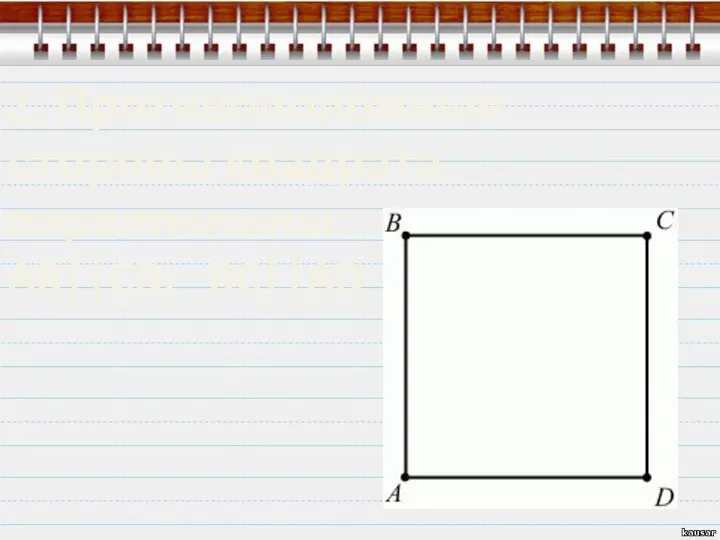
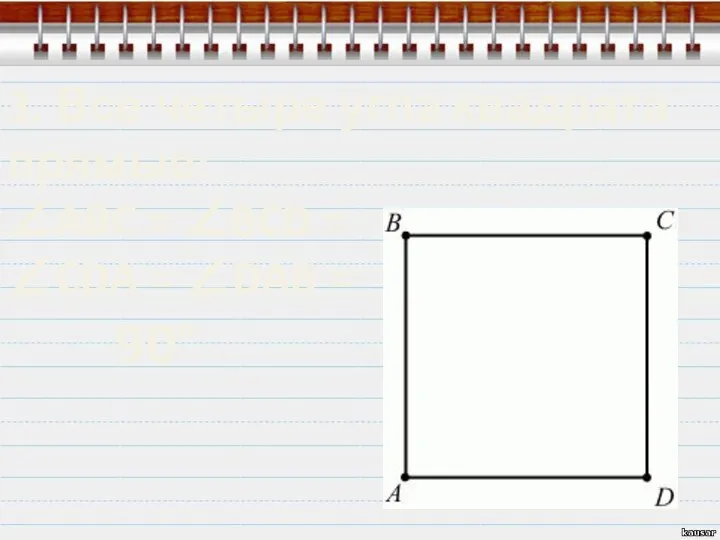
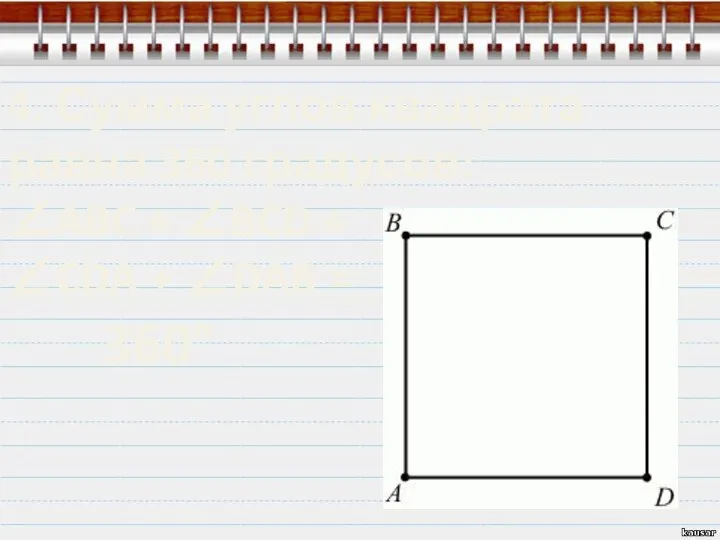
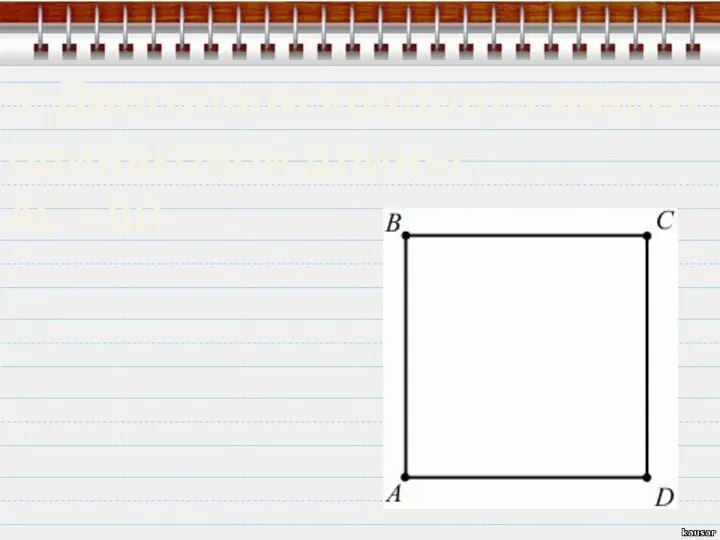
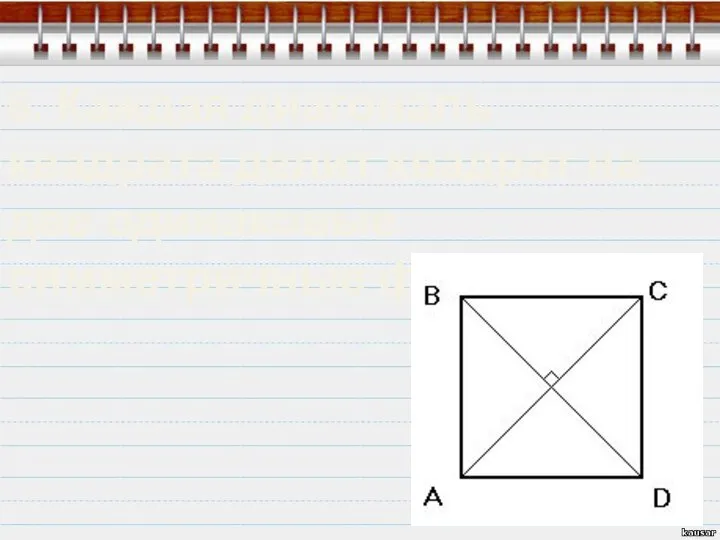
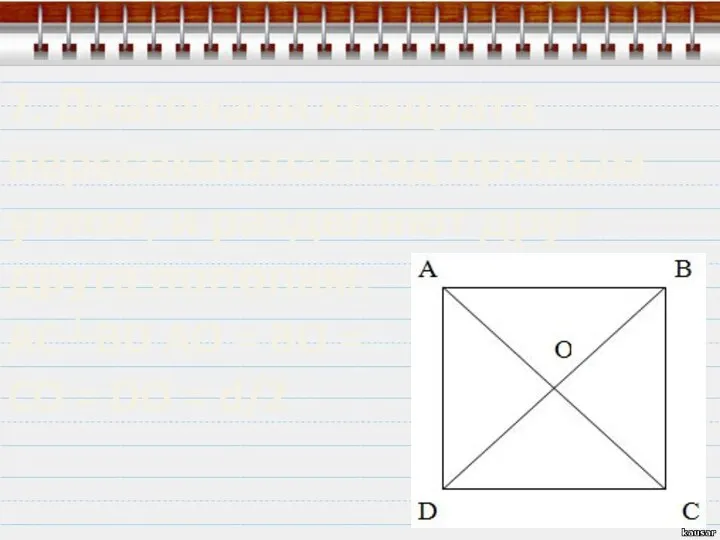
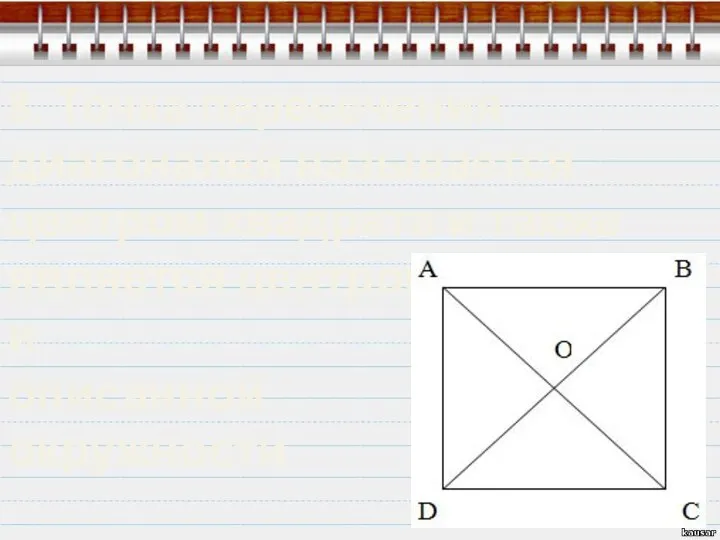
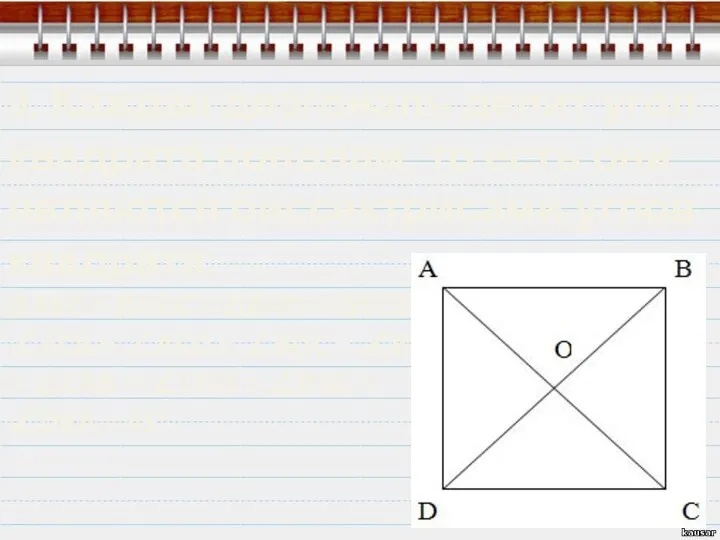
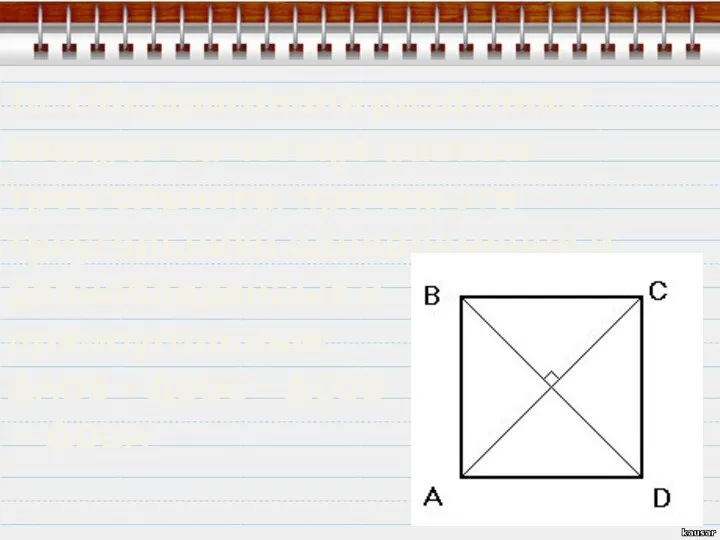

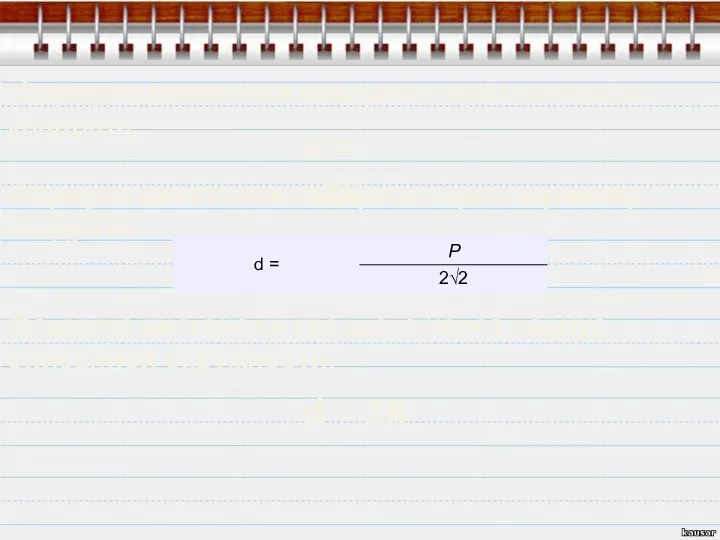





 Таблица умножения числа 2 и на 2
Таблица умножения числа 2 и на 2 Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1
Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1 Статистический анализ результатов мониторинга
Статистический анализ результатов мониторинга Вынесение общего множителя за скобки. 6 класс
Вынесение общего множителя за скобки. 6 класс Степень с натуральным показателем. Задания
Степень с натуральным показателем. Задания Решение уравнений. Элективный курс. Алгебра 11 класс. Урок 2
Решение уравнений. Элективный курс. Алгебра 11 класс. Урок 2 Принадлежность точки выделенной области. 10 класс
Принадлежность точки выделенной области. 10 класс Уравнения, системы уравнений. Задание №9
Уравнения, системы уравнений. Задание №9 Теория расписаний. Минимизация приоритето-порождающих функций
Теория расписаний. Минимизация приоритето-порождающих функций Математическое описание случайных явлений
Математическое описание случайных явлений Операции над множествами
Операции над множествами Презентация на тему Занимательная математика (5 класс)
Презентация на тему Занимательная математика (5 класс)  Учимся считать. Интерактивный тренажёр
Учимся считать. Интерактивный тренажёр Упрощение выражений
Упрощение выражений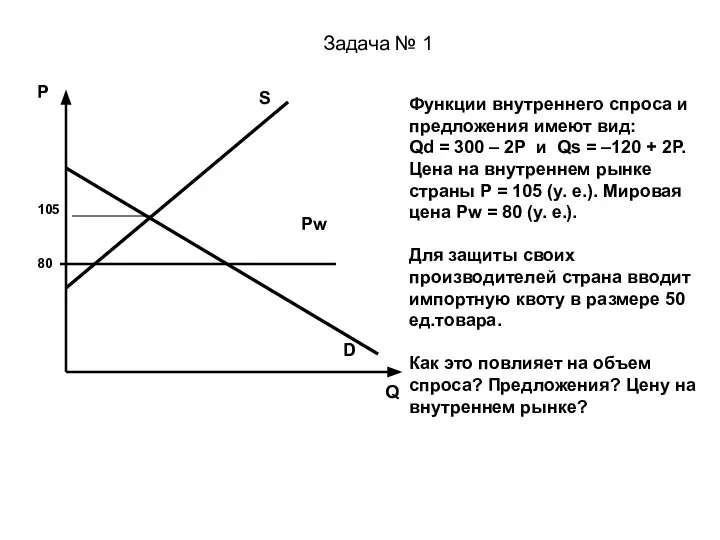 Функции внутреннего спроса и предложения. Разбор задач
Функции внутреннего спроса и предложения. Разбор задач Презентация на тему Свойства логарифмов (10 класс)
Презентация на тему Свойства логарифмов (10 класс)  Математика в профессии сварщика
Математика в профессии сварщика Задачи на перебор вариантов
Задачи на перебор вариантов Прикладной количественный анализ заголовков
Прикладной количественный анализ заголовков Путешествие в историю математики. Решение старинных задач
Путешествие в историю математики. Решение старинных задач Прямоугольные треугольники
Прямоугольные треугольники История развития экономико-математических методов (ЭММ) и моделей. Лекция 1
История развития экономико-математических методов (ЭММ) и моделей. Лекция 1 Презентацию подготовила Кулагина В.В. Учитель начальных классов ФКОУ СОШ имени А.Н.Радищева Г. Кузнецк-12 2012г.
Презентацию подготовила Кулагина В.В. Учитель начальных классов ФКОУ СОШ имени А.Н.Радищева Г. Кузнецк-12 2012г. Округление десятичных дробей. Опорные конспекты
Округление десятичных дробей. Опорные конспекты Подборка заданий по геометрии за курс 7 класса
Подборка заданий по геометрии за курс 7 класса Задачи с цифрами 1, 5, 9
Задачи с цифрами 1, 5, 9 Математика в медицине
Математика в медицине Векторное произведение векторов
Векторное произведение векторов