Квадратичная функция, ее график и свойства

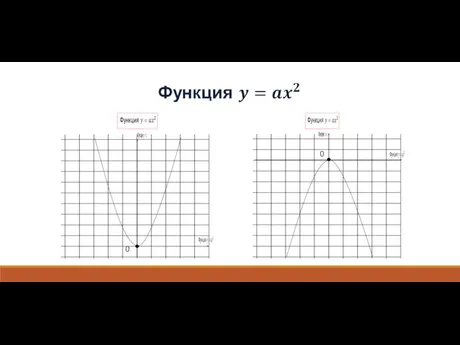
Графиком функции
при любом а = 0 является парабола с вершиной в начале координат
Ось симметрии – Ось ординат
При а > 0 ветви параболы направлены вверх
При а < 0 ветви параболы направлены вниз

Определение.
Функция вида у = ах2+bх+с,
где а, b, c – заданные числа,
а ≠ 0, х – действительная переменная, называется квадратичной функцией.

Графиком функции у = ах2+bх+с
при любом а = 0 является парабола
При а > 0 ветви параболы направлены вверх
При а < 0 ветви параболы направлены вниз

1. Коэффициент а влияет на направление ветвей параболы:
при а > 0 – ветви направлены вверх,
при а < 0 – вниз.
2. Коэффициент b влияет на расположение вершины параболы:
при b = 0 вершина лежит на оси ОУ.
3. Коэффициент с показывает точку пересечения параболы с осью ОУ.

Найти координаты вершины параболы:

Найти координаты вершины параболы:

Алгоритм построения графика функции

найти Область определения функции
найти Область значения функции
Определить промежутки, в которых функция возрастает/убывает
Определить промежутки, в которых функция принимает положительные/отрицательные значения
Определить наибольшее (наименьшее) значение параболы
Алгоритм исследования графика функции

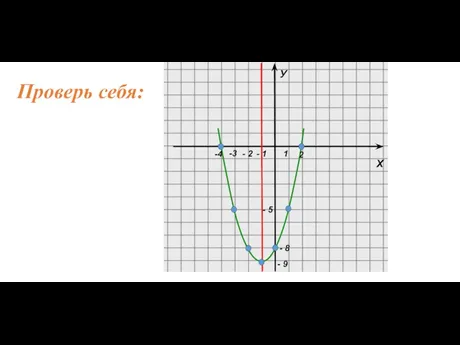
Построить график функции
y = х2 + 2х - 8

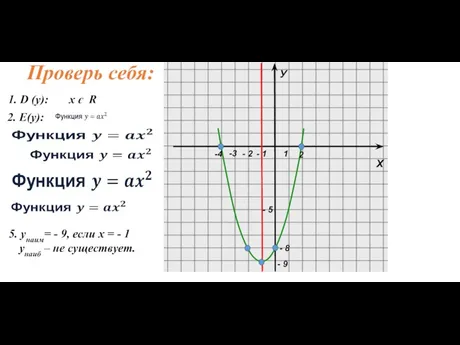
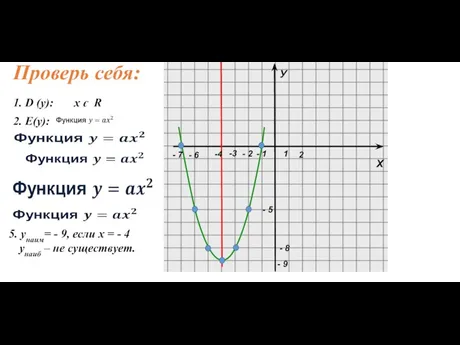
1. Ветви параболы направлены вверх, т. к. а = 1 (1>0)
Проверь себя:
2. Вершина параболы: т. А (-1; - 9)
4. Нули функции:
Точки пересечения с ОХ : (- 4; 0); (2; 0)
Точки пересечения с ОУ : (0; - 8)
3. Ось симметрии: х0 = - 1
5.
y = х2 + 2х - 8

Х
У
Проверь себя:
-4
-3
1
- 2
- 1
- 9
- 8
- 5
2

Х
У
Проверь себя:
-4
-3
1
- 2
- 1
- 9
- 8
- 5
2
1. D (y): x є R
2. Е(y):
5. унаим= - 9, если х = - 1
унаиб – не существует.

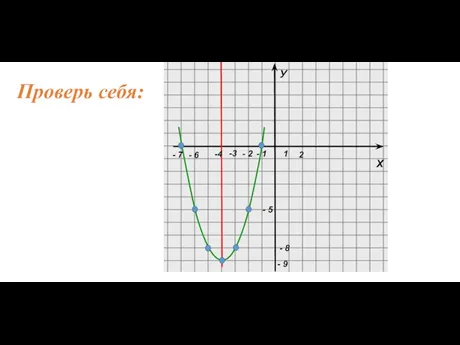
Построить график функции
y = х2 + 8х + 7

1. Ветви параболы направлены вверх, т. к. а = 1 (1>0)
Проверь себя:
2. Вершина параболы: т. А (-4; - 9)
4. Нули функции:
Точки пересечения с ОХ : (- 7; 0); (- 1; 0)
Точки пересечения с ОУ : (0; 7)
3. Ось симметрии: х0 = - 4
5.
y = х2 + 8х + 7

Х
У
Проверь себя:
-4
-3
1
- 2
- 1
- 9
- 8
- 5
2
- 7
- 6

Х
У
Проверь себя:
-4
-3
1
- 2
- 1
- 9
- 8
- 5
2
- 7
- 6
1. D (y): x є R
2. Е(y):
5. унаим= - 9, если х = - 4
унаиб – не существует.

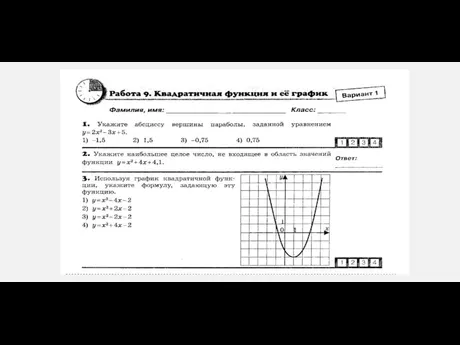
Не выполняя построения графика функции у = - 4х2 + 4х + 3, , определите направление её ветвей.
Не выполняя построения графика функции, найдите значение х, при котором функция у = - 4х2 + 4х + 3 принимает наибольшее значение, и найдите это значение
Не выполняя построения графика функции у = - 4х2 + 4х + 3, , определите промежутки возрастания (убывания) функции
Резервное задание: